Краткие теоретические сведения.
Тема 1. Определители.
Квадратной матрицей порядка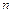 называется квадратная таблица из чисел
называется квадратная таблица из чисел 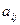 (
(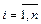 ,
,  ):
): 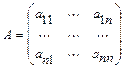 , состоящая из
, состоящая из 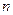 строк и
строк и 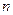 столбцов. У квадратной матрицы различают главную диагональ:
столбцов. У квадратной матрицы различают главную диагональ: 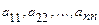 и побочную диагональ:
и побочную диагональ:  . Любой квадратной матрице
. Любой квадратной матрице 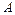 порядка
порядка 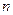 можно поставить в соответствие число
можно поставить в соответствие число  , равное алгебраической сумме
, равное алгебраической сумме  слагаемых, составленных определённым образом из элементов
слагаемых, составленных определённым образом из элементов 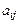 матрицы
матрицы 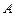 ,называемое определителем матрицы. Кратко обозначается
,называемое определителем матрицы. Кратко обозначается 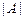 ,
,  .
.
Определителем 1-ого порядка называется число 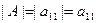 .
.
Определителем 2-ого порядка называется число
 .
.
Определителем 3-его порядка называется число 
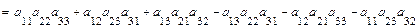 .
.
Минором элемента 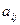 называется определитель
называется определитель , полученный из определителя
, полученный из определителя  вычёркиванием
вычёркиванием 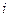 -ой строки и
-ой строки и  -ого столбца.
-ого столбца.
Алгебраическим дополнением 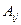 элемента
элемента 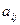 называется его минор
называется его минор  , взятый со знаком
, взятый со знаком  :
:
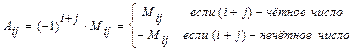 .
.
Определителем порядка 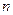 называется число
называется число

Разложением определителя  по
по 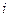 -ой строке (
-ой строке (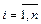 ) называется соотношение:
) называется соотношение: 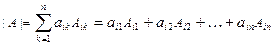 .
.
Разложением определителя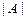 по
по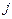 -ому столбцу (
-ому столбцу ( ) называется соотношение:
) называется соотношение: 
Определители обладают следующими свойствами:
1) определитель не изменится при замене всех его строк столбцами с теми же номерами;
2) определитель изменит знак на противоположный, если переставить местами любые две строки (два столбца) определителя;
3) общий множитель элементов какой-либо строки (столбца) можно вынести за знак определителя;
4) определитель равен нулю, если он содержит нулевую строку (столбец), две одинаковые или пропорциональные строки (столбца);
5) определитель не изменится, если к какой-либо строке (столбцу) прибавить другую строку (столбец), умноженную на любое число;
6) определитель треугольного вида (когда все элементы, лежащие по одну сторону одной из его диагоналей равны нулю) равен произведению диагональных элементов:  .
.
Тема 2. Матрицы.
Матрицей размера  называется прямоугольная таблица из чисел
называется прямоугольная таблица из чисел 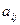 (
( ,
,  ):
): 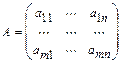 , состоящая из
, состоящая из 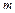 строк и
строк и 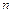 столбцов. Если необходимо указать размеры матрицы, то пишут
столбцов. Если необходимо указать размеры матрицы, то пишут 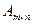 .
.
Если 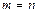 , то матрица
, то матрица 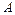 называется квадратной.
называется квадратной.
Нулевой называется матрица  , все элементы которой равны нулю, например:
, все элементы которой равны нулю, например:  . Единичной называется квадратная матрица
. Единичной называется квадратная матрица 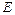 , на главной диагонали которой стоят единицы, а все остальные элементы равны нулю, например:
, на главной диагонали которой стоят единицы, а все остальные элементы равны нулю, например: 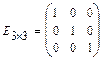 . Треугольной называется квадратная матрица
. Треугольной называется квадратная матрица 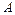 , все элементы которой расположенные по одну сторону от главной диагонали равны нулю, например:
, все элементы которой расположенные по одну сторону от главной диагонали равны нулю, например: 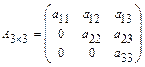 . Трапециевидной (ступенчатой) называется матрица
. Трапециевидной (ступенчатой) называется матрица 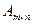
 , все элементы которой, расположенные ниже элементов
, все элементы которой, расположенные ниже элементов 
 равны нулю, например:
равны нулю, например: 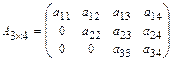 .
.
Матрицы 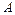 и
и  называются равными и пишут
называются равными и пишут  , если они одинакового размера и их соответствующие элементы равны:
, если они одинакового размера и их соответствующие элементы равны: 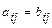 ,
, ,
, .
.
Матрицы можно транспонировать, складывать, вычитать, умножать на число, умножать на другую матрицу.
Транспонированной к матрице 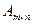 называется матрица
называется матрица 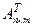 , столбцами которой являются соответствующие строки матрицы
, столбцами которой являются соответствующие строки матрицы 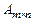 .
.
Суммой (разностью) матриц 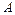 и
и  одного размера
одного размера  , называется матрица
, называется матрица  того же размера, для которой:
того же размера, для которой:
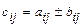 ,
,  ,
, .
.
Произведением матрицы 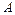 размера
размера  на число
на число  называется матрица
называется матрица  того же размера, для которой:
того же размера, для которой: 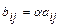 ,
,  ,
,  .
.
Линейной комбинацией матриц 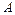 и
и одного размера
одного размера  , называется матрица
, называется матрица  того же размера (
того же размера (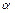 и
и  - произвольные числа), для которой:
- произвольные числа), для которой: 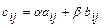 ,
,  ,
, ,
,
Произведением матрицы 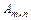 на матрицу
на матрицу 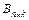 называется матрица
называется матрица 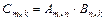 , каждый элемент которой
, каждый элемент которой 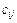 вычисляется по правилу:
вычисляется по правилу:
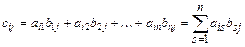 ,
,  ,
, 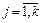 .
.
Операция умножения матрицы на матрицу определена не для всех матриц, а только для таких у которых число столбцов левой матрицы 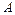 равно числу строк правой матрицы
равно числу строк правой матрицы  . Такие матрицы называются согласованнымидля умножения. Поэтому прежде чем выполнять операцию умножения матрицы на матрицу следует проверить их согласованность для умножения и определить размерность матрицы-произведения (если умножение матриц возможно):
. Такие матрицы называются согласованнымидля умножения. Поэтому прежде чем выполнять операцию умножения матрицы на матрицу следует проверить их согласованность для умножения и определить размерность матрицы-произведения (если умножение матриц возможно):  . Особенность операции умножения матриц состоит в том, что в общем случае:
. Особенность операции умножения матриц состоит в том, что в общем случае:  , т.е. переместительное свойство места не имеет.
, т.е. переместительное свойство места не имеет.
Элементарными преобразованиями матрицы называются:
1) перестановка строк (столбцов);
2) умножение строки (столбца) на число, отличное от нуля;
3) прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число;
4) вычёркивание нулевой строки (столбца).
Матрицы 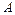 и
и  , полученные одна из другой в результате элементарных преобразований называются эквивалентнымии пишут
, полученные одна из другой в результате элементарных преобразований называются эквивалентнымии пишут  .
.
Обратнойк квадратной матрице 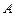 порядка
порядка  , называется матрица
, называется матрица 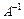 того же порядка, если:
того же порядка, если:  , где
, где 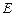 - единичная матрица порядка
- единичная матрица порядка  .
.
Квадратная матрица 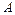 называется невырожденной, если её определитель
называется невырожденной, если её определитель  . Обратная матрица всегда существует для невырожденных матриц.
. Обратная матрица всегда существует для невырожденных матриц.
Основными методами вычисления обратной матрицы являются:
Метод присоединённой матрицы. Если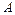 -невырожденная матрица, то
-невырожденная матрица, то 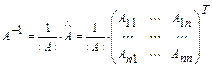 , где
, где  - присоединённая матрица, для которой:
- присоединённая матрица, для которой: 
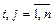 . Здесь
. Здесь 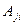 - алгебраические дополнения элементов
- алгебраические дополнения элементов  матрицы
матрицы 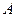 .
.
В частности, если 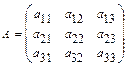 , то
, то 
Метод элементарных преобразований. Для данной квадратной матрицы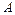 порядка
порядка 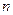 строится прямоугольная матрица
строится прямоугольная матрица  размера
размера 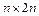 приписыванием к
приписыванием к 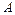 справа единичной матрицы. Далее, с помощью элементарных преобразований над строками, матрица
справа единичной матрицы. Далее, с помощью элементарных преобразований над строками, матрица  приводится к виду
приводится к виду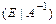 , что всегда возможно, если
, что всегда возможно, если 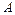 - невырожденная.
- невырожденная.
Матричными называются уравнения вида:  ,
,  ,
, 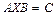 ,
,
где матрицы - известны, матрица
- известны, матрица 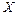 - неизвестна. Если квадратные матрицы
- неизвестна. Если квадратные матрицы 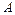 и
и  - невырожденные, то решения матричных уравнений записываются, соответственно, в виде:
- невырожденные, то решения матричных уравнений записываются, соответственно, в виде: 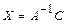 ,
,  ,
,  .
.
Минором  -ого порядка матрицы
-ого порядка матрицы 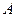 размера
размера  называется определитель
называется определитель  квадратной матрицы порядка
квадратной матрицы порядка  , образованной элементами матрицы
, образованной элементами матрицы 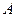 , стоящими на пересечении произвольно выбранных её
, стоящими на пересечении произвольно выбранных её 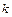 строк и
строк и 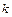 столбцов
столбцов  . Максимальный порядок
. Максимальный порядок 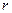 отличных от нуля миноров матрицы
отличных от нуля миноров матрицы 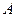 , называется её рангом и обозначается
, называется её рангом и обозначается 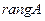 или
или  , а любой минор порядка
, а любой минор порядка 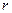 , отличный от нуля – базисным минором.
, отличный от нуля – базисным минором.
Тема 3. Системы линейных уравнений.
…Система уравнений вида:  называется системой
называется системой 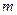 линейных уравнений с
линейных уравнений с 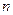 неизвестными. Числа
неизвестными. Числа 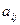 называются коэффициентами системы,
называются коэффициентами системы, 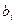 - свободными членами системы,
- свободными членами системы,  - неизвестными системы.
- неизвестными системы.
В матричной форме система имеет вид:  , где
, где  ,
,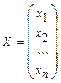 ,
,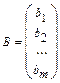 .Здесь
.Здесь 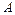 -матрица системы,
-матрица системы, 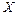 -матрица-столбец неизвестных,
-матрица-столбец неизвестных, -матрица-столбец свободных членов.
-матрица-столбец свободных членов.
Если  , то система называется однородной, в противном случае неоднородной.
, то система называется однородной, в противном случае неоднородной.
Система, матрица 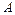 которой является треугольной с диагональными элементами
которой является треугольной с диагональными элементами  , называется треугольной. Система, матрица
, называется треугольной. Система, матрица 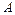 которой является трапециевидной, называется трапециевидной.
которой является трапециевидной, называется трапециевидной.
Решением системы называется всякий упорядоченный набор чисел  , обращающий каждое уравнение системы в равенство. Совокупность всех решений называется множеством решений системы.
, обращающий каждое уравнение системы в равенство. Совокупность всех решений называется множеством решений системы.
Система называется совместной, если она имеет, по крайней мере, одно решение; определённой, если она имеет только одно решение; неопределённой, если она имеет бесконечно много решений; несовместной, если она не имеет решений.
Однородная система уравнений всегда совместна, так как всегда имеет, по крайней мере, нулевое решение 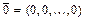 . Треугольная система является определённой, трапециевидная система – неопределённой.
. Треугольная система является определённой, трапециевидная система – неопределённой.
Две системы называются эквивалентными, если множества их решений совпадают.
Элементарными преобразованиями систем уравнений называются:
1) перестановка уравнений;
2) перестановка местами слагаемых  в каждом из уравнений системы;
в каждом из уравнений системы;
3) умножение уравнения на число, отличное от нуля;
4)прибавление к уравнению другого, умноженного на любое число;
5) вычёркивание уравнения вида:  .
.
Основными точными методами решения систем линейных уравнений являются методы: Крамера, обратной матрицы и Гаусса.
Если число уравнений в системе 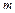 совпадает с числом неизвестных
совпадает с числом неизвестных 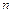 и определитель матрицы системы
и определитель матрицы системы  , то система имеет единственное решение, которое можно найти:
, то система имеет единственное решение, которое можно найти:
а) методом Крамера по формулам: 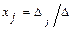 ,
,  , где
, где  - определитель, получаемый из определителя матрицы системы
- определитель, получаемый из определителя матрицы системы 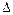 заменой
заменой 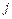 -ого столбца на столбец свободных членов;
-ого столбца на столбец свободных членов;
б) методом обратной матрицы по формуле  .
.
Методом Гаусса находят решение произвольной системы линейных уравнений. Метод состоит в приведении системы уравнений, с помощью элементарных преобразований, к системе специального вида, эквивалентной исходной, решение которой очевидно. Преобразования по методу Гаусса выполняют в два этапа. Первый этап называют прямым ходом, второй - обратным.
В результате прямого хода выясняют: совместна или нет система и если совместна то, сколько имеет решений - одно или бесконечно много, а также, в случае бесконечного множества решений, указывают базисные и свободные неизвестные для записи общего решения системы. Преобразования прямого хода выполняют, как правило, над расширенной матрицей системы  , которую получают, приписывая справа к матрице системы
, которую получают, приписывая справа к матрице системы 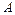 столбец свободных членов
столбец свободных членов  . В результате элементарных преобразований строк и перестановкой столбцов, матрица системы
. В результате элементарных преобразований строк и перестановкой столбцов, матрица системы 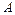 должна быть приведена к матрице
должна быть приведена к матрице 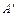 треугольного или трапециевидного вида с элементами
треугольного или трапециевидного вида с элементами  . При этом, система уравнений, матрица которой
. При этом, система уравнений, матрица которой 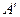 , является треугольной с диагональными элементами
, является треугольной с диагональными элементами 
 , будет иметь единственное решение; система уравнений, матрица которой
, будет иметь единственное решение; система уравнений, матрица которой 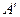 , является трапециевидной с элементами
, является трапециевидной с элементами 
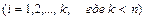 , будет иметь бесконечно много решений. Если, при выполнении преобразований расширенной матрицы
, будет иметь бесконечно много решений. Если, при выполнении преобразований расширенной матрицы  , в преобразованной матрице
, в преобразованной матрице 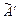 появится строка
появится строка 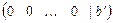 , где
, где  , то это говорит о несовместности исходной системы уравнений. Базисные неизвестные указывают, выписывая базисный минор преобразованной матрицы системы
, то это говорит о несовместности исходной системы уравнений. Базисные неизвестные указывают, выписывая базисный минор преобразованной матрицы системы 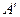 . Базисными являются неизвестные преобразованной системы, столбцы коэффициентов
. Базисными являются неизвестные преобразованной системы, столбцы коэффициентов  при которых образуют базисный минор (определитель максимального порядка, отличный от нуля). Свободными являются неизвестные, не являющиеся базисными.
при которых образуют базисный минор (определитель максимального порядка, отличный от нуля). Свободными являются неизвестные, не являющиеся базисными.
В результатеобратного хода находят решение системы, записывая его в виде общего решения, если их бесконечно много. Преобразования обратного хода часто выполняют, над уравнениями системы, соответствующей последней расширенной матрице 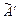 прямого хода. В случае единственного решения, его получают, находя последовательно значения всех неизвестных из уравнений системы, начиная с последнего. В случае, когда решений бесконечно много, их записывают в виде общего решения. Для этого свободным неизвестным придают разные произвольные постоянные значения:
прямого хода. В случае единственного решения, его получают, находя последовательно значения всех неизвестных из уравнений системы, начиная с последнего. В случае, когда решений бесконечно много, их записывают в виде общего решения. Для этого свободным неизвестным придают разные произвольные постоянные значения: 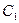 ,
, 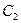 ,…,
,…, 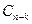 , и последовательно из уравнений системы, начиная с последнего, находят значения всех базисных неизвестных. Полученное решение называют общим. Придавая произвольным постоянным, конкретные значения, находят частные решения системы уравнений.
, и последовательно из уравнений системы, начиная с последнего, находят значения всех базисных неизвестных. Полученное решение называют общим. Придавая произвольным постоянным, конкретные значения, находят частные решения системы уравнений.
Тема 4. Системы векторов. N-мерное векторное пространство. Евклидово пространство.
Арифметическим вектором называют упорядоченную совокупность из 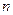 чисел:
чисел:  и обозначают
и обозначают 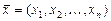 . Числа
. Числа  называют компонентами вектора
называют компонентами вектора 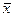 , число компонент называют его размерностью.
, число компонент называют его размерностью.
Векторы  и
и 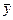 называют равными, если они одинаковой размерности и их соответствующие компоненты равны:
называют равными, если они одинаковой размерности и их соответствующие компоненты равны:  ,
,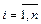 .
.
Суммой векторов  и
и 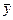 одной размерности, называют вектор
одной размерности, называют вектор 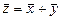 той же размерности, для которого:
той же размерности, для которого:  ,
, 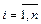 .
.
Произведением вектора 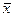 на число
на число  называют вектор
называют вектор  той же размерности, для которого:
той же размерности, для которого:  ,
, 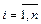 .
.
Линейной комбинациейвекторов 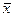 и
и  одной размерности, называют вектор
одной размерности, называют вектор 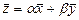 той же размерности (
той же размерности (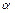 и
и  - произвольные числа), для которого:
- произвольные числа), для которого:  ,
, 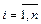 .
.
Множество всех 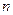 -мерных векторов, в котором введены операции сложения и умножения на число, удовлетворяющие определённым требованиям (аксиомам) называют векторнымпространствоми обозначают
-мерных векторов, в котором введены операции сложения и умножения на число, удовлетворяющие определённым требованиям (аксиомам) называют векторнымпространствоми обозначают  .
.
Систему векторов  называют линейно зависимой, если найдутся числа
называют линейно зависимой, если найдутся числа 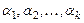 ,
,  одновременно, такие, что
одновременно, такие, что 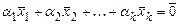 (где
(где  - нулевой вектор), в противном случае, систему называют линейно независимой.
- нулевой вектор), в противном случае, систему называют линейно независимой.
Базисом системы векторов  называют упорядоченную систему векторов
называют упорядоченную систему векторов 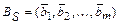 , удовлетворяющую условиям:
, удовлетворяющую условиям:
1)  ,
,  ; 2) система
; 2) система 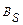 линейно независима; 3) для любого вектора
линейно независима; 3) для любого вектора  найдутся числа
найдутся числа 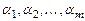 такие, что
такие, что 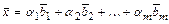 . Коэффициенты
. Коэффициенты  , однозначно определяемые вектором
, однозначно определяемые вектором 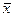 , называют координатами вектора в базисе
, называют координатами вектора в базисе 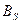 , а формулу называют разложениемвектора
, а формулу называют разложениемвектора 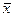 по базису
по базису 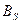 и пишут:
и пишут:  .
.
В пространстве  базисом является каждая упорядоченная система из
базисом является каждая упорядоченная система из 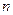 линейно независимых векторов:
линейно независимых векторов: 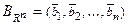 . Формулу
. Формулу 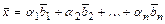 называют разложениемвектора
называют разложениемвектора 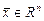 по базису
по базису  , коэффициенты
, коэффициенты 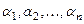 - координатами вектора в базисе
- координатами вектора в базисе и пишут
и пишут 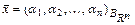 .
.
Всякая упорядоченная система из 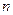 векторов
векторов  образует базис
образует базис  , если определитель, столбцами которого являются компоненты векторов
, если определитель, столбцами которого являются компоненты векторов 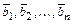 , не равен нулю.
, не равен нулю.
Пространство  , в котором введено скалярное произведение векторов, удовлетворяющее определённым требованиям (аксиомам), называют евклидовым. Скалярным произведением двух векторов
, в котором введено скалярное произведение векторов, удовлетворяющее определённым требованиям (аксиомам), называют евклидовым. Скалярным произведением двух векторов  и
и  называют число:
называют число:  .
.
Тема 5. Линейные операторы. Собственные числа и векторы.
Операторомназывается закон (правило), по которому каждому вектору 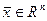 ставится в соответствие единственный вектор
ставится в соответствие единственный вектор  , и пишут
, и пишут  или
или  В дальнейшем, рассматривается случай
В дальнейшем, рассматривается случай  (преобразование пространства
(преобразование пространства ). Оператор
). Оператор  называется линейным, если для любых векторов
называется линейным, если для любых векторов 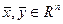 и действительных чисел
и действительных чисел  выполнено условие:
выполнено условие: 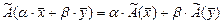 .
.
Если 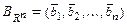 - базис пространства
- базис пространства  , томатрицей линейного оператора
, томатрицей линейного оператора  в базисе
в базисе 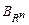 называется квадратная матрица
называется квадратная матрица 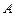 порядка
порядка 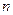 , столбцами которой являются столбцы координат векторов
, столбцами которой являются столбцы координат векторов 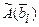 . Между линейными операторами, действующими в
. Между линейными операторами, действующими в  и квадратными матрицами порядка
и квадратными матрицами порядка 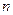 , существует взаимно однозначное соответствие, что позволяет оператор
, существует взаимно однозначное соответствие, что позволяет оператор  представить в матричном виде
представить в матричном виде  , где
, где  - матрицы-столбцы координат векторов
- матрицы-столбцы координат векторов  ,
, 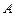 - матрица оператора
- матрица оператора  в базисе
в базисе 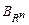 .
.
Для линейных операторов, действующих в  вводятся следующие операции: 1) сложение операторов:
вводятся следующие операции: 1) сложение операторов: ; 2) умножение операторов на число:
; 2) умножение операторов на число: ; 3) умножение операторов:
; 3) умножение операторов:  .
.
Обратным к оператору  называется оператор
называется оператор  такой, что
такой, что  , где
, где 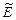 - единичный (тождественный)оператор, реализующий отображение
- единичный (тождественный)оператор, реализующий отображение 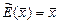 . Обратный оператор
. Обратный оператор  существует только для невырожденных операторов
существует только для невырожденных операторов  (операторов, матрица которых является невырожденной). Все, рассмотренные выше, действия над линейными операторами выполняют, выполняя аналогичные действия над их матрицами.
(операторов, матрица которых является невырожденной). Все, рассмотренные выше, действия над линейными операторами выполняют, выполняя аналогичные действия над их матрицами.
Пусть число  и вектор
и вектор 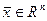 ,
, 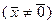 , таковы, что выполняются равенства:
, таковы, что выполняются равенства: 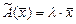 или
или 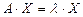 . Тогда число
. Тогда число  называется собственным числом линейного оператора
называется собственным числом линейного оператора  (или матрицы
(или матрицы 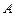 ), а вектор
), а вектор 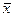 - собственным вектором этого оператора (или матрицы), соответствующим собственному числу
- собственным вектором этого оператора (или матрицы), соответствующим собственному числу  . Равенство
. Равенство 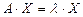 может быть записано в виде
может быть записано в виде  , где
, где 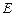 - единичная матрица порядка
- единичная матрица порядка 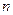 ,
, 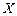 - матрица-столбец координат собственного вектора
- матрица-столбец координат собственного вектора 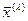 , соответствующего собственному числу
, соответствующего собственному числу  ,
, 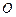 - нулевая матрица-столбец.
- нулевая матрица-столбец.
Характеристическим уравнением оператора  (или матрицы
(или матрицы 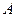 ) называется уравнение:
) называется уравнение: 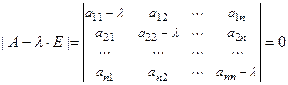 .
.
Множество собственных чисел оператора (или матрицы) совпадает с множеством корней его характеристического уравнения:  , а множество собственных векторов, отвечающих собственному числу
, а множество собственных векторов, отвечающих собственному числу 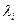 , совпадает с множеством ненулевых решений матричного уравнения:
, совпадает с множеством ненулевых решений матричного уравнения: 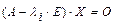 .
.
Тема 6. Квадратичные формы.
Квадратичной формой  ( или кратко
( или кратко  ) от
) от 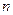 -переменных называется однородный многочлен второй степени с действительными коэффициентами:
-переменных называется однородный многочлен второй степени с действительными коэффициентами:  , где
, где 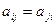 . Квадратичную форму всегда можно записать в матричном виде:
. Квадратичную форму всегда можно записать в матричном виде: 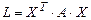 , где
, где 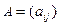 - матрица квадратичной формы (являющаяся симметрической, так как выполняется условие
- матрица квадратичной формы (являющаяся симметрической, так как выполняется условие 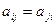 ),
), 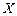 - матрица-столбец,
- матрица-столбец, 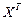 - матрица-строка, составленные из переменных
- матрица-строка, составленные из переменных 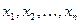 .
.
Квадратичная форма называется невырожденной, если её матрица является невырожденной.
Квадратичная форма называется канонической, если она имеет вид:
 .
.
Всякую квадратичную форму всегда можно привести к каноническому виду, например, методами Лагранжа и ортогональных преобразований.
Квадратичные формы подразделяют на различные типы в зависимости от множества их значений. Квадратичная форма  называется:
называется:
положительно (отрицательно) определённой, если для любого 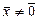 выполняется неравенство
выполняется неравенство 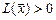 (
( ); неотрицательно (неположительно) определённой, если для любого
); неотрицательно (неположительно) определённой, если для любого 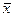 выполняется неравенство
выполняется неравенство 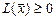 (
(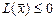 ), причём существует
), причём существует 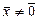 , для которого
, для которого  ; знакопеременной (или неопределённой), если существуют такие
; знакопеременной (или неопределённой), если существуют такие 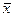 и
и  , что
, что 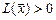 и
и 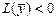 .
.
Невырожденная квадратичная форма может быть либо положительно определённой, либо отрицательно определённой, либо знакопеременной. Тип невырожденной квадратичной формы можно определить, проверяя знаки главных миноров матрицы квадратичной формы.
Пусть 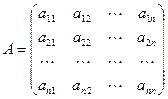 , где
, где 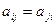 - матрица квадратичной формы. Главными минорами матрицы
- матрица квадратичной формы. Главными минорами матрицы 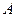 называются миноры порядка
называются миноры порядка 
(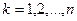 ), составленные из первых
), составленные из первых  строк и первых
строк и первых  столбцов матрицы:
столбцов матрицы: 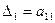 ,
, 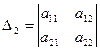 ,
,  ,
, 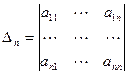 .
.
Критерием знакоопределённости невырожденной квадратичной формы является критерий Сильвестра:
- квадратичная форма  положительно определена тогда и только тогда, когда все главные миноры её матрицы положительны, т.е.
положительно определена тогда и только тогда, когда все главные миноры её матрицы положительны, т.е. 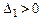 ,
,  ,
,  ,
, 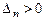 ;
;
- квадратичная форма  отрицательно определена тогда и только тогда, когда для всех главных миноров её матрицы выполняются неравенства:
отрицательно определена тогда и только тогда, когда для всех главных миноров её матрицы выполняются неравенства: 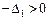 ,
,  ,
,  ,
,  ,
, 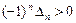 (все миноры нечётного порядка отрицательны, а чётного – положительны) ;
(все миноры нечётного порядка отрицательны, а чётного – положительны) ;
- квадратичная форма  знакопеременна тогда и только тогда, когда для главных миноров её матрицы выполняется хотя бы одно из условий: один из главных миноров равен нулю, один из главных миноров чётного порядка отрицателен, два главных минора нечётного порядка имеют разные знаки .
знакопеременна тогда и только тогда, когда для главных миноров её матрицы выполняется хотя бы одно из условий: один из главных миноров равен нулю, один из главных миноров чётного порядка отрицателен, два главных минора нечётного порядка имеют разные знаки .
Тема 7. Векторная алгебра.
Вектором (геометрическим) называется направленный отрезок, задаваемый упорядоченной парой точек (началом и концом вектора). Обозначают вектор 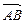 или
или  . Расстояние между началом и концом вектора называется его длиной и обозначается
. Расстояние между началом и концом вектора называется его длиной и обозначается 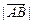 или
или  . Углом между векторами
. Углом между векторами  и
и 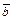 называется угол
называется угол 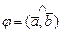 ,
,  , на который следует повернуть один из векторов, чтобы его направление совпало с направлением другого вектора, при условии, что их начала совпадают. Проекцией вектора
, на который следует повернуть один из векторов, чтобы его направление совпало с направлением другого вектора, при условии, что их начала совпадают. Проекцией вектора  на вектор
на вектор 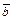 называется число
называется число 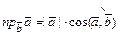 .
.
Векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Векторы называются компланарными, если они расположены в одной плоскости или в параллельных плоскостях.
Векторы 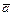 и
и 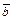 называются равными и пишут
называются равными и пишут  , если они коллинеарны, одинаково направлены и имеют равные длины. Векторы
, если они коллинеарны, одинаково направлены и имеют равные длины. Векторы  и
и 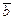 называются противоположными и пишут
называются противоположными и пишут  , если они коллинеарны, направлены в разные стороны и имеют равные длины.
, если они коллинеарны, направлены в разные стороны и имеют равные длины.
Суммой векторов  и
и 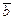 называется вектор
называется вектор 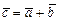 , соединяющий начало вектора
, соединяющий начало вектора  и конец вектора
и конец вектора 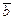 , при условии, что конец вектора
, при условии, что конец вектора  совпадает с началом вектора
совпадает с началом вектора 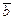 (правило треугольника). Произведением вектора
(правило треугольника). Произведением вектора  на действительное число
на действительное число  называется вектор
называется вектор  :
:
1) коллинеарный вектору  ; 2) имеющий длину
; 2) имеющий длину 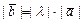 ; 3) направленный одинаково с вектором
; 3) направленный одинаково с вектором  , если
, если 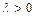 , и противоположно, если
, и противоположно, если  .
.
Ортом вектора  , называется вектор
, называется вектор 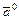 , имеющий единичную длину и направление вектора
, имеющий единичную длину и направление вектора  :
: 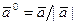 .
.
Базисом в пространстве  называется упорядоченная тройка некомпланарных векторов, базисом на плоскости
называется упорядоченная тройка некомпланарных векторов, базисом на плоскости 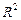 – упорядоченная пара неколлинеарных векторов, базисом на прямой
– упорядоченная пара неколлинеарных векторов, базисом на прямой 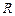 – любой ненулевой вектор на этой прямой. Базис, в котором все векторы попарно перпендикулярны и имеют единичную длину, называется ортонормированным. Векторы ортонормированного базиса обозначаются:
– любой ненулевой вектор на этой прямой. Базис, в котором все векторы попарно перпендикулярны и имеют единичную длину, называется ортонормированным. Векторы ортонормированного базиса обозначаются: 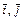 и
и  , и называются базисными ортами. Различают правый и левый ортонормированные базисы. Базис
, и называются базисными ортами. Различают правый и левый ортонормированные базисы. Базис 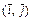 -называется правым, если кратчайший поворот от
-называется правым, если кратчайший поворот от  к
к  совершается против хода часовой стрелки, в противном случае он – левый. Базис
совершается против хода часовой стрелки, в противном случае он – левый. Базис 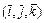 -называется правым, если из конца вектора
-называется правым, если из конца вектора  кратчайший поворот от вектора
кратчайший поворот от вектора  к
к