Вычисление определителя и обратной матрицы
Вычисление определителя матрицы является классическим примером задач, для решения которых важно найти эффективные алгоритмы.
При непосредственном раскрытии определителя квадратной матрицы n-го порядка надо найти сумму n! слагаемых, каждое из которых равно произведению n элементов матрицы, взятых по одному с каждого столбца и каждой строки, т.е. надо выполнить порядка n!n операций. Число операций для вычисления определителя 100-го порядка приблизительно равно 100!∙100 ≈ 100157,9∙100. Такое число операций не способен выполнить ни один из существующих суперкомпьютеров. Тем не менее, современные компьютерные программы вычисления определителей справляются с матрицами и более высокого порядка, используя экономичные алгоритмы. Одним из таких алгоритмов является метод Гаусса.
Если матрица приведена к диагональному или треугольному виду, то её определитель равен произведению диагональных элементов.
Для преобразования матрицы к треугольному виду можно применить метод Гаусса, что потребует порядка 2n3/3 операций. Для n = 100 имеем 2n3/3 ≈ 0,67∙106. На такой объем арифметических операций современный персональный компьютер тратит не более одной секунды.
Если внимательно проанализировать метод Гаусса, то можно увидеть, что он фактически позволяет одновременно с приведением матрицы коэффициентов к треугольному виду, вычислить определитель этой матрицы. Действительно, определитель матрицы коэффициентов системы уравнений (3.18) равен произведению диагональных элементов, т.е. равен единице. С другой стороны, если к любой строке матрицы прибавить другую строку, умноженную на число, то определитель не изменится. А если строку матрицы разделить на число, отличное от нуля, то определитель матрицы разделится на то же число. Отсюда следует, что в результате преобразований виду (3.18), определитель матрицы коэффициентов системы уравнений (3.9) изменился на множитель, который равен произведению ведущих элементов, т.е. мы получаем формулу для вычисления определителя
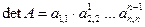 .
.
Метод Гаусса также эффективен и для вычисления обратной матрицы. Вычисление обратной матрицы можно рассматривать как частный случай решения совокупности систем линейных уравнений с одной и той же матрицей коэффициентов и разными правыми частями. В этом случае преобразования, которые применяются к столбцу b правых частей системы, нужно применить к нескольким столбцам правых частей.
Пример 3.8. Для заданной матрицы вычислить определитель и обратную матрицу.
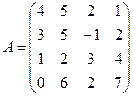 .
.
Решение.Используем рабочий лист решения примера 3.3. Введем элементы данной матрицы в диапазоне A2:D5.
В ячейке G17 вычислим произведение ведущих элементов (т.е. тех чисел, на которые делили строки), для этого введем формулу =A2*B7*C12*D17. В ячейку F17 введем формулу =МОПРЕД(A2:D5) и убедимся в правильности результата. Получим значение –190.
Для вычисления обратной матрицы используем новый рабочий лист.
Рассмотрим расширенную матрицу
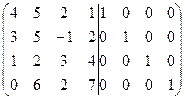
Мы должны преобразовать методом Гаусса исходную матрицу к единичной, тогда единичная матрица справа от вертикальной черты преобразуется к обратной матрице.
Прямой ход метода Гаусса.
0. Запишем элементы матрицы в диапазоне A2:D5 и элементы единичной матрицы в диапазоне E2:H5.
1. В ячейку A7 вводим формулу =A2/$A2; выделим A7 и протянем маркер заполнения до ячейки H7.
Затем в ячейку A8 вводим формулу =A3-A$7*$A3; выделим A8 и протянем маркер заполнения до H8.
Выделим строку A8:H8 и протянем маркером заполнения вниз до строки 10.
В ячейках A7:HE10 появятся следующие значения:
| 1,0000 | 1,2500 | 0,5000 | 0,2500 | 0,2500 | 0,0000 | 0,0000 | 0,0000 |
| 0,0000 | 1,2500 | -2,5000 | 1,2500 | -0,7500 | 1,0000 | 0,0000 | 0,0000 |
| 0,0000 | 0,7500 | 2,5000 | 3,7500 | -0,2500 | 0,0000 | 1,0000 | 0,0000 |
| 0,0000 | 6,0000 | 2,0000 | 7,0000 | 0,0000 | 0,0000 | 0,0000 | 1,0000 |
2. Присвоим строке A12:H12 значения строки A7:H7:
Выделим диапазон A12:H12, введем формулу =A7:H7 и удерживая нажатыми клавиши Ctrl и Shift, нажимаем Enter (Ctrl + Shift + Enter).
В ячейку B13 вводим формулу =B8/$B8; выделим B13 и протянем маркер заполнения до H13.
Затем в ячейку B14 вводим формулу =B9-B$13*$B9; выделим B14 и протянем мышью маркер заполнения до H14.
Выделим диапазон B14:H14 и протянем маркер заполнения до H15.
В ячейках A12:H15 появятся следующие значения:
| 1,0000 | 1,2500 | 0,5000 | 0,2500 | 0,2500 | 0,0000 | ||
| 0,0000 | 1,0000 | -2,0000 | 1,0000 | -0,6000 | 0,8000 | 0,0000 | 0,0000 |
| 0,0000 | 4,0000 | 3,0000 | 0,2000 | -0,6000 | 1,0000 | 0,0000 | |
| 0,0000 | 14,0000 | 1,0000 | 3,6000 | -4,8000 | 0,0000 | 1,0000 |
3. Перепишем значения строк A12:H15 в строки A17:H18, для этого выделим диапазон A12:H15, введем формулу =A12:H13 и удерживая клавиши Ctrl и Shift нажатыми, нажимаем Enter.
В ячейку C19 вводим формулу =C14/$C14; выделим C19 и протянем мышью за правый нижний угол до H19.
В ячейку C20 вводим формулу =C15-C$19*$C15, выделим C20 и протянем маркер заполнения до H20. В ячейках A17:H20 получим значения:
| 1,0000 | 1,2500 | 0,5000 | 0,2500 | 0,2500 | 0,0000 | ||
| 0,0000 | 1,0000 | -2,0000 | 1,0000 | -0,6000 | 0,8000 | ||
| 1,0000 | 0,7500 | 0,0500 | -0,1500 | 0,2500 | 0,0000 | ||
| 0,0000 | -9,5000 | 2,9000 | -2,7000 | -3,5000 | 1,0000 |
4. Осталось разделить последнюю строку на ведущий элемент. Сформируем в диапазоне A22:H25 матрицы, которые получаются после применения прямого хода метода Гаусса.
Выделим диапазон A22:H24 и введем формулу =A17:H19 и, удерживая нажатыми клавиши Ctrl и Shift, нажимаем Enter. В ячейку D25 вводим формулу =D20/$D20, выделим D25 и протянем мышью за правый нижний угол до H25. В диапазоне A22:H25 получим:
| 1,0000 | 1,2500 | 0,5000 | 0,2500 | 0,2500 | 0,0000 | ||
| 0,0000 | 1,0000 | -2,0000 | 1,0000 | -0,6000 | 0,8000 | ||
| 0,0000 | 0,0000 | 1,0000 | 0,7500 | 0,0500 | -0,1500 | 0,25 | |
| 1,0000 | -0,3053 | 0,2842 | 0,3684 | -0,1053 |
Далее применим обратный ход метода Гаусса.
5. Выделим A30:H30, введем =A25:H25 и нажмем комбинацию клавиш Ctrl + Shift + Enter. В ячейку D29 введем =D24-D$25*$D24, выделим D29 и протянем маркер заполнения вправо до H29. А затем снова выделим D29 и протянем маркер заполнения влево до A29. Теперь выделим всю строку A29:H29 и протянем вверх до строки 27.
6. Выделим A34:H35, введем =A29:H30 и нажмем комбинацию клавиш Ctrl + Shift + Enter. В ячейку C33 введем =C28-C$34*$C28, выделим C33 и протянем маркер заполнения вправо до H33. А затем снова выделим C33 и протянем маркер заполнения влево до A33. Теперь выделим всю строку A33:H33 и протянем маркером заполнения на одну строку вверх до строки 32.
7. Выделим A38:H40, введем формулу =A33:H35 и нажмем комбинацию клавиш Ctrl + Shift + Enter. В ячейку B37 введем формулу =B32-B$38*$B32, выделим B37 и протянем маркер заполнения вправо до H37. Затем снова выделим B37 и протянем маркер заполнения влево в ячейку A37.
В диапазоне A37:D40 получена единичная матрица, а в диапазоне E37:H40 — обратная:
| A | B | C | D | E | F | G | H | |
| -0,14211 | 0,373684 | 0,447368 | -0,34211 | |||||
| 0,263158 | -0,21053 | -0,42105 | 0,263158 | |||||
| 0,278947 | -0,36316 | -0,02632 | 0,078947 | |||||
| -0,30526 | 0,284211 | 0,368421 | -0,10526 |
Для проверки полученного результата выделим диапазон A43:D46, введем формулу =МУМНОЖ(A2:D5;E37:H40) и нажмем комбинацию клавиш Ctrl + Shift + Enter. Получим единичную матрицу.
Приведем программу на языке C++ для вычисления определителя матрицы методом Гаусса с выбором главного элемента.
#include <except.h>
#include <iostream.h>
long double detA(long double **a, const int n);
int main(){
long double **a; long double dA; int i,j,n;
cout <<" input n = " ; cin >> n;
try {
a= new long double*[n]; for(i=0;i<n;i++) a[i]=new long double[n];
}
catch (xalloc){cout <<"nCould not allocaten"; exit(-1);}
cout <<"n input matrix a n";
for (i=0; i<n; i++)for (j=0; j<n; j++)cin >> a[i][j];
dA = detA(a, n);
cout << "n matrix a: ";
for (i=0; i<n; i++){cout << "n"; for (j=0; j<n; j++) cout <<" "<< a[i][j];}
cout << "n determinant A = "; cout << dA;
cout << "n Press Key and Enter to continue";
cin >> i; // for pause
for(i=0;i<n;i++)delete[] a[i];
delete a;
return 0;
}//end main
long double detA(long double **a, const int n){
long double **aa;
int i, k, m, im; long double amm, aim, r,d;
try {aa= new long double*[n];
for(i=0;i<n;i++) aa[i]=new long double[n]; }
catch (xalloc){cout <<"nCould not allocaten"; exit(-1);}
for (i = 0; i <= n-1; i++)
for (k = 0; k <= n-1; k++) aa[i][k] = a[i][k];
d = 1;
for (m = 0; m <= n-2; m++) {// m
amm = aa[m][m]; im = m;
for (i = m; i <= n-1; i++)
if(aa[i][m] > amm){amm = aa[i][m]; im = i; } d = d*amm;
if(im != m)d = - d;
cout <<"n amm = "<<amm;
if(im != m)for (k = m; k <= n-1; k++)
{r = aa[im][k]; aa[im][k] = aa[m][k]; aa[m][k] = r;}
for (k = m; k <= n-1; k++)aa[m][k] = aa[m][k]/amm; // 3.16
for (i = m + 1; i <= n-1; i++){// i
aim = aa[i][m];
for (k = m; k <= n-1; k++)
aa[i][k] = aa[i][k] - aa[m][k]*aim; // 3.17
}// end i
}// end m
d = d* aa[n-1][n-1]; cout <<"n amm = "<< aa[n-1][n-1];
for(i=0;i<n;i++)delete[] aa[i];
delete aa;
return d;
}// end detA
Отметим, что в данной программе исходная матрица a[][] сохраняется, так как для преобразований в подпрограмме-функции detA() используется дополнительный массив aa[][]. Все используемые массивы динамические, их размерность задается во время выполнения программы.
Приведем результат расчета определителя по этой программе:
input n = 4
input matrix a
4 5 2 1 3 5 -1 2 1 2 3 4 0 6 2 7 [столбец чисел ]
amm = 4
amm = 6
amm = 2.25
amm = 3.51852
matrix a:
4 5 2 1
3 5 -1 2
1 2 3 4
0 6 2 7
Determinant A = –190
Press key and Enter to continue
Приведем теперь программу вычисления обратной матрицы методом Гаусса с выбором главного элемента:
#include <except.h>
#include <iostream.h>
int Matr_inv(long double **a, long double **a1, const int n);
int main(){
long double **a; long double **ainv; int i,j,n;
cout <<" input n = " ; cin >> n;
try {
ainv= new long double*[n]; for(i=0;i<n;i++) ainv[i]=new long double[n];
}
catch (xalloc){cout <<"nCould not allocaten"; exit(-1);}
try {
a= new long double*[n]; for(i=0;i<n;i++) a[i]=new long double[n];
}
catch (xalloc){cout <<"nCould not allocaten"; exit(-1);}
cout <<"n input matrix a n";
for (i=0; i<n; i++)for (j=0; j<n; j++)cin >> a[i][j];
cout << "n matrix a: ";
for (i=0; i<n; i++){cout << "n";
for (j=0; j<n; j++) cout <<" "<< a[i][j];}
Matr_inv(a, ainv, n);
cout << "n ------------------- matr a: ";
for (i=0; i<n; i++){cout << "n";
for (j=0; j<n; j++) cout <<" "<< a[i][j];}
cout << "n -------------------- inv matr ainv: ";
for (i=0; i<n; i++){cout << "n";
for (j=0; j<n; j++) cout <<" "<< ainv[i][j];}
cout << "n Press Key and Enter to continue";
cin >> i; // for pause
for(i=0;i<n;i++)delete[] a[i];
delete a;
for(i=0;i<n;i++)delete[] ainv[i];
delete ainv;
return 0;
}//end main
int Matr_inv(long double **a, long double **a1, const int n){
int i, k, m, im; long double amm, aim, r;
for (i = 0; i <= n-1; i++)
for (k = 0; k <= n-1; k++){
if(i==k)a1[i][k] = 1; else a1[i][k] = 0;}
// 1.
for (m = 0; m <= n-2; m++) {// m
amm = a[m][m]; im = m;
for (i = m; i <= n-1; i++)
if(a[i][m] > amm){amm = a[i][m]; im = i; }
if(im != m){
for (k = m; k <= n-1; k++){
r = a[im][k]; a[im][k] = a[m][k]; a[m][k] = r;}
for (k = 0; k <= n-1; k++){
r = a1[im][k]; a1[im][k] = a1[m][k]; a1[m][k] = r;}
}
for (k = m; k <= n-1; k++)a[m][k] = a[m][k]/amm;
for (k = 0; k <= n-1; k++) a1[m][k] = a1[m][k]/amm;
for (i = m + 1; i <= n-1; i++){// i
aim = a[i][m];
for (k = m; k <= n-1; k++)a[i][k] = a[i][k] - a[m][k]*aim;
for (k = 0; k <= n-1; k++)a1[i][k] = a1[i][k] - a1[m][k]*aim;
}// end i
}// end m
// 2.
amm = a[n-1][n-1]; a[n-1][n-1] = 1;
for (k = 0; k <= n-1; k++) a1[n-1][k] = a1[n-1][k]/amm;
for (m = n-1; m >= 0; m--){
for (i = m-1; i >= 0; i--){// i
aim = a[i][m]; a[i][m] = 0;
for (k = 0; k <= n-1; k++)a1[i][k] = a1[i][k] - a1[m][k]*aim;
}// end i
}// end m
return 0;
}// end Matr_inv
Подпрограмма Matr_inv(a, a1, n) не сохраняет исходную матрицу. В результате выполнения программы в массиве a формируется единичная матрица, а в массиве a1 — обратная матрица. Приведем результат выполнения программы для примера 3.8:
input n = 4
input matrix a
4 5 2 1 3 5 -1 2 1 2 3 4 0 6 2 7 [столбец чисел ]
matrix a
4 5 2 1
3 5 -1 2
1 2 3 4
0 6 2 7
---------------------------- matr a
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 0
---------------------------- inv matr ainv
-0,142105 0,373684 0,447368 -0,342105
0,263158 -0,210526 -0,421053 0,263158
0,278947 -0,363158 -0,0263158 0,0789474
-0,305263 0,284211 0,368421 -0,105263
Press Key and Enter to continue
Как видим, результат совпадает с обратной матрицей, найденной в программе Excel обычным методом Гаусса.