Понятие многочлена
Многочленом называется  с коэффициентами
с коэффициентами  из некоторого поля P.Здесь
из некоторого поля P.Здесь  - степень одночлена. Наибольшая из степеней одночленов называется степенью многочлена.
- степень одночлена. Наибольшая из степеней одночленов называется степенью многочлена.
Суммой двух многочленов называется многочлен, коэффициенты которого есть сумма соответствующих коэффициентов многочленов.
Произведение многочленов сводится к попарному произведению всех слагаемых и приведению подобных.
Говорят, что многочлен f делит многочлен g (f|g), если существует многочлен h, такой что g=fh
Свойства делимости:
1)Если f|g и g|h, то f|h
2)Если f|g и f|h, то f|(g +h)
3)Если f|g,то для любого h: f|gh
4)Пусть 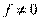 и
и  и
и  . Тогда если f|g, то
. Тогда если f|g, то 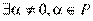 , такое что
, такое что 
5) Если f|g и g|f, 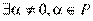

Доказательство:
1)  , то есть f|h
, то есть f|h
2) 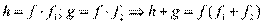 , то есть f|(g +h)
, то есть f|(g +h)
3) 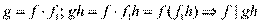
4) 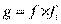 , откуда очевидно, что
, откуда очевидно, что 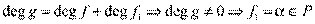 и
и 
5) 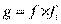 и
и 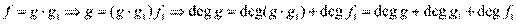
Теорема о делении с остатком.
Определение. Пусть  и
и 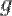 — многочлены,
— многочлены,  . Будем говорить, что
. Будем говорить, что  поделен на
поделен на 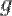 с остатком, если
с остатком, если  представлен в виде
представлен в виде 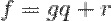 , где
, где  и
и  — многочлены, причем
— многочлены, причем 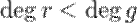 .
.
Полином  называется остатком от деления
называется остатком от деления  на
на 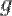 ,
,  — неполным частным.
— неполным частным.
Теорема. (о делении с остатком). Пусть  и
и 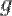 — полиномы над полем
— полиномы над полем  ,
, 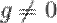 . Тогда существуют единственные многочлены
. Тогда существуют единственные многочлены  и
и  над полем
над полем  такие, что
такие, что 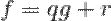 и
и 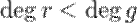 .
.
Доказательство. Существование.
Пусть 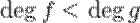 . Положим
. Положим  .
.
 .
.
Предположим, что теорема верна не для любого полинома  (
(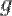 фиксируем). Среди всех многочленов
фиксируем). Среди всех многочленов  , для которых теорема неверна, выберем многочлен наименьшей степени и обозначим его
, для которых теорема неверна, выберем многочлен наименьшей степени и обозначим его 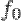 :
:

Пусть 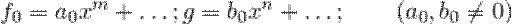 . Положим
. Положим

Коэффициент при  в многочлене
в многочлене 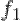 равен
равен 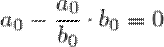 . Следовательно,
. Следовательно, 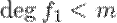 . Значит, для многочлена
. Значит, для многочлена 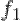 теорема верна. Существуют такие
теорема верна. Существуют такие 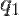 и
и  , что
, что 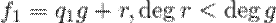 . Тогда
. Тогда

Получили противоречие с тем предположением, что есть многочлены, для которых теорема неверна.
Единственность. Предположим, что
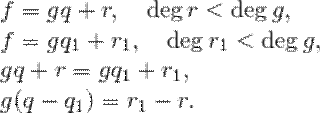
1)  . Значит,
. Значит,  ,
,
2) 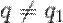 .
.
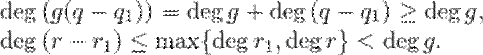
Получили противоречие. Этот случай невозможен.