НОД двух многочленов

Многочлен d называется наибольшим общим делителем многочленов f и g, если

1) d делит f и d делит g

2) если существует многочлен h, который также делит f и g, то h делит d.

Свойства НОД:

1) Если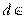НОД(f , g), то степень d максимальна среди степеней всех общих делителей

2) Для любого h НОД(f , g)=НОД(f -gh, g)

Доказательство:

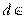1) Действительно, произвольный общий делитель многочленов f и g степенью не превосходит НОД(f , g)

2) Пусть 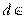НОД(f , g) и 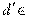НОД(f -gh, g). Тогда:

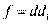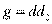
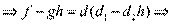
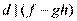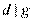
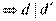
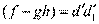и и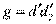

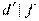и и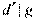

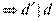
Тогда 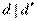и 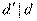, значит по свойству делимости (5)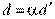 НОД(f -gh, g), что и требовалось.

Деление многочленов (с остатком). Если P(x) и Q(x) – многочлены по x степеней n и m соответственно, 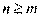, то всегда существуют однозначно определенные многочлены T(x) степени (n-m) и R(x) степени меньше, чем m, такие что тождественно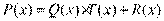

Теорема: (Алгоритм Евклида)

Для нахождения НОД (наибольшего общего делителя) двух многочленов a(x) и b(x) выполняется цепочка делений до получения остатка, равного нулю:

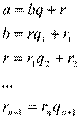
Тогда r_n – наибольший общий делитель многочленов a и b.

Доказательство: согласно свойству НОД (2) имеем:

НОД(a,b)=НОД(a-bq, b)=НОД(r,b)=…=НОД()=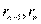

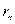
Многочлен называется неприводимым, если его нельзя разложить в произведение многочленов меньших степеней.

Теорема: Основная теорема арифметики многочленов

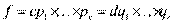
Всякий многочлен над полем представим в виде произведения неприводимых многочленов, причем такое произведение единственно: 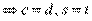, 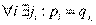и 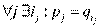- биекция.

Теорема о разложении многочлена на неприводимые множители: Всякий многочлен разлагается на неприводимые множители однозначно с точностью до множителей нулевой степени.

Другая формулировка:

Елси многочлен f(x) из кольца P[x] двумя спсобами разложен в произведение неприводимых множителей:

(1), то s=t и, при соответствующей нумерации, имеют место равенства

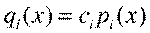(2), i=1,2,...,s, где сi - отличные от нуля элементы из поля P.

Доказательство: эта теорема верна для многочленов первой степени, так как они неприводимы. Мы будем поэтому вести доказательство индукцией по степени многочлена, т.е. будем доказывать теорему для f(x), предполагая, что для многочленов меньшей степени она уже доказана.

Так как q1(x) является делителем для f(x), то q1(x) будет делителем хотя бы одного из многочленов pi(x), например для p1(x). Так как, многочлен р1(ч) неприводим, а степень q1(x) больше нуля, то существует такой элемент с1,что

q1(x)=c1p1(x) (3). Подставляя это выражение q1(x) в (1) и сокращая на р1(х) (что законно, так как в кольце P[x] нет делителей нуля), мы получим равенство

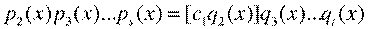. Так как степень многочлена, равного этим произведениям, меньше степени f(x), то уже доказано, что s-1=t-1, откуда s=t, и что существует такие элементы 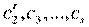, что 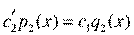, откуда 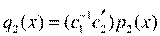и 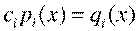, i=3,...,s. Полагая 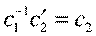и учитывая (3), мы полностью получим равенства (2).