Базис и размерность
Пусть V – векторное пространство над полем P и  . А – линейно полное (или система образующих, или система порождающих), если любой вектор из V выражается линейно через конечное множество векторов из А.
. А – линейно полное (или система образующих, или система порождающих), если любой вектор из V выражается линейно через конечное множество векторов из А.
Теорема: об очистке линейно полного множества
Пусть А – линейно полное и 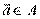 линейно выражается через другие элементы из А. Тогда
линейно выражается через другие элементы из А. Тогда 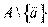 - линейно полное.
- линейно полное.
Базисом пространства называется линейно полное множество линейно независимых векторов в этом пространстве.
Теорема: о выборе базиса
Из каждого конечного полного множества векторов можно выбрать базис.
Теорема: о дополнении до базиса
Пусть в пространстве есть конечный базис. Тогда всякое конечное линейно независимое множество векторов 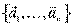 можно дополнить до конечного базиса пространства, причём в качестве дополняющих векторов взять векторы из любого конечного базиса
можно дополнить до конечного базиса пространства, причём в качестве дополняющих векторов взять векторы из любого конечного базиса 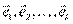 .
.
Теорема: критерий базиса
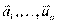 - базис в векторного пр-ва V
- базис в векторного пр-ва V  любой вектор из V единственным образом выраж. через
любой вектор из V единственным образом выраж. через 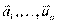 .
.
Если число векторов базиса конечно, то пространство называется конечномерным, а число базисных векторов – размерностью (dim V) этого пространства. Если базис не является конечным множеством, то пространство называется бесконечномерным.
Теорема: корректность определения
Доказательство: из всех базисов выберем наименьший. Он непуст, т.к. 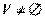 . Обозначим базисные векторы через
. Обозначим базисные векторы через 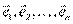 . В другом базисе есть
. В другом базисе есть 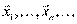 . Рассмотрим
. Рассмотрим 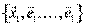 - линейно полное, но линейно зависимое множество, т.к.
- линейно полное, но линейно зависимое множество, т.к. 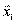 по определению базиса выражается через
по определению базиса выражается через 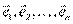 . Значит, по критерию базиса, есть
. Значит, по критерию базиса, есть 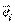 , которое выражается через
, которое выражается через 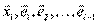 , поэтому исключаем из базиса
, поэтому исключаем из базиса 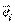 :
: 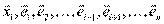 . Это множество линейно независимо, т.к. в противном случае при выкидывании ещё одного вектора мы получили бы базис из (n-1) вектора, но в исходном базисе было n векторов и он был самым маленьким – противоречие.
. Это множество линейно независимо, т.к. в противном случае при выкидывании ещё одного вектора мы получили бы базис из (n-1) вектора, но в исходном базисе было n векторов и он был самым маленьким – противоречие.
Теперь рассмотрим 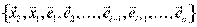 и т.д. В итоге базис
и т.д. В итоге базис 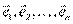 превратится в базис
превратится в базис 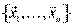 , так как каждый раз мы вводим в базис вектор
, так как каждый раз мы вводим в базис вектор 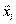 и исключаем из базиса
и исключаем из базиса 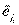 . Получим, что
. Получим, что 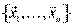 - базис. Значит, во всех базисах одинаковое количество векторов.
- базис. Значит, во всех базисах одинаковое количество векторов.