Пары форм.
Пусть дана пара действительных квадратичных форм от 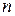 неизвестных,
неизвестных, 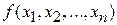 и
и  . Существует ли такое невырожденное линейное преобразование неизвестных
. Существует ли такое невырожденное линейное преобразование неизвестных 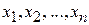 , которое одновременно приводило бы обе эти формы к каноническому виду?
, которое одновременно приводило бы обе эти формы к каноническому виду?
В общем случае ответ будет отрицательным. Рассмотрим, например, пару форм
 .
.
Пусть существует невырожденное линейное преобразование
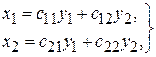
приводящее обе эти формы к каноническому виду. Для того чтобы форма 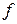 могла быть приведена указанным преобразованием к каноническому виду, один из коэффициентов
могла быть приведена указанным преобразованием к каноническому виду, один из коэффициентов  должен быть равен нулю, иначе вошло бы слагаемое
должен быть равен нулю, иначе вошло бы слагаемое  . Меняя, если нужно, нумерацию неизвестных
. Меняя, если нужно, нумерацию неизвестных  , можно положить, что
, можно положить, что  и поэтому
и поэтому 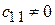 . Мы получим теперь, однако, что
. Мы получим теперь, однако, что
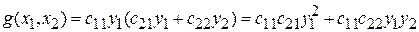 .
.
Так как форма  также должна была перейти в канонический вид, то
также должна была перейти в канонический вид, то 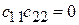 , т. е.
, т. е.  , что вместе с
, что вместе с  противоречит невырожденности указанного линейного преобразования.
противоречит невырожденности указанного линейного преобразования.
Ситуация будет иной, если мы положим, что хотя бы одна из наших форм, например  , является положительно определенной.
, является положительно определенной.
ТЕОРЕМА. Если 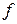 и
и 
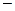 пара действительных квадратичных форм от
пара действительных квадратичных форм от 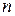 неизвестных, причем вторая из них положительно определенная, то существует невырожденное линейное преобразование, одновременно приводящее форму
неизвестных, причем вторая из них положительно определенная, то существует невырожденное линейное преобразование, одновременно приводящее форму  к нормальному виду, а форму
к нормальному виду, а форму 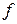 к каноническому виду.
к каноническому виду.
ДОКАЗАТЕЛЬСТВО. Выполним сначала невырожденное линейное преобразование неизвестных  ,
,
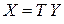 ,
,
приводящее положительно определенную форму  к нормальному виду,
к нормальному виду,
 .
.
Форма 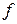 перейдет при этом в некоторую форму
перейдет при этом в некоторую форму 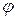 от новых неизвестных,
от новых неизвестных,
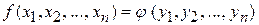 .
.
Совершим теперь ортогональное преобразование неизвестных  ,
,
 ,
,
приводящее форму 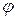 к главным осям,
к главным осям,
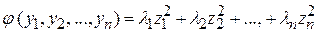 .
.
Это преобразование переводит сумму квадратов неизвестных  в сумму квадратов неизвестных
в сумму квадратов неизвестных 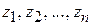 (что следует из формулы
(что следует из формулы 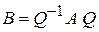 ). В результате мы получаем
). В результате мы получаем
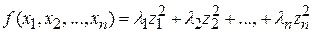 ,
,
 .
.
т. е. линейное преобразование

является искомым. □