Эквивалентностью их характеристических матриц.
Как известно [1], две квадратные матрицы порядка 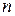 подобны тогда и только тогда, когда они задают один и тот же линейный оператор в разных базисах. Однако мы не можем пока ответить на вопрос, подобны ли данные числовые матрицы
подобны тогда и только тогда, когда они задают один и тот же линейный оператор в разных базисах. Однако мы не можем пока ответить на вопрос, подобны ли данные числовые матрицы 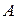 и
и 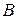 (т. е. матрицы с элементами из основного поля
(т. е. матрицы с элементами из основного поля  ). Тем не менее, их характеристические матрицы
). Тем не менее, их характеристические матрицы 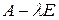 и
и 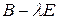 являются
являются  матрицами, и вопрос об эквивалентности этих матриц решается вполне эффективно. Ответ на вопрос о связи подобия числовых матриц с эквивалентностью их характеристических матриц даёт следующая
матрицами, и вопрос об эквивалентности этих матриц решается вполне эффективно. Ответ на вопрос о связи подобия числовых матриц с эквивалентностью их характеристических матриц даёт следующая
ТЕОРЕМА. Матрицы 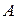 и
и 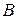 с элементами из поля
с элементами из поля  тогда и только тогда подобны, когда их характеристические матрицы
тогда и только тогда подобны, когда их характеристические матрицы 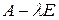 и
и 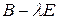 эквивалентны.
эквивалентны.
ДОКАЗАТЕЛЬСТВО. Пусть матрицы 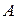 и
и 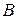 подобны, т. е. над полем
подобны, т. е. над полем  существует такая невырожденная матрица
существует такая невырожденная матрица 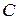 , что
, что
 .
.
Тогда
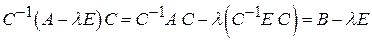 .
.
Невырожденные числовые матрицы 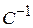 и
и 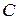 являются, однако, унимодулярными
являются, однако, унимодулярными  матрицами. Матрица
матрицами. Матрица 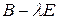 получена умножением матрицы
получена умножением матрицы 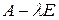 слева и справа на унимодулярные матрицы, т. е.
слева и справа на унимодулярные матрицы, т. е. 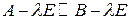 .
.
Обратно, пусть
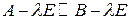 .
.
Тогда существуют такие унимодулярные матрицы 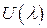 и
и 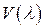 , что
, что
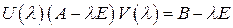 . (1)
. (1)
Учитывая, что для унимодулярных матриц обратные матрицы существуют и являются  матрицами, выведем из (1) равенства, которые будут использованы в дальнейшем для доказательства:
матрицами, выведем из (1) равенства, которые будут использованы в дальнейшем для доказательства:
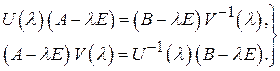 (2)
(2)
Так как  матрица
матрица 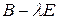 имеет по
имеет по 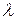 степень
степень 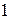 , причем старшим коэффициентом соответствующего матричного многочлена служит невырожденная матрица
, причем старшим коэффициентом соответствующего матричного многочлена служит невырожденная матрица 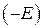 , то к матрицам
, то к матрицам 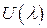 и
и 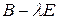 можно применить алгоритм деления с остатком. Значит, существуют такие матрицы
можно применить алгоритм деления с остатком. Значит, существуют такие матрицы  и
и 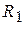 , причём, степень
, причём, степень 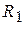 , если
, если 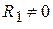 , равна
, равна 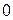 по
по 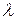 , что
, что
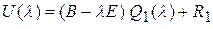 . (3)
. (3)
Аналогично
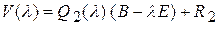 . (4)
. (4)
Используя (3) и (4) и учитывая (1), получаем:
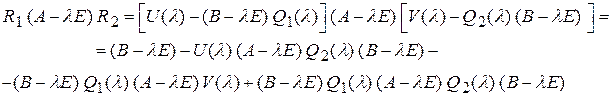
или, применяя (2),
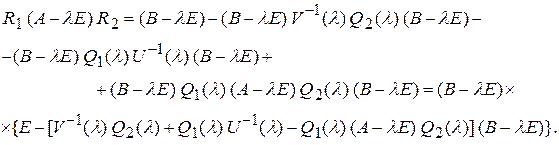
Квадратная скобка, стоящая справа, равна в действительности нулю: в противном случае она, являясь  матрицей, так как и
матрицей, так как и 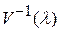 и
и 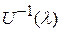 есть
есть  матрицы, имела бы по меньшей мере степень
матрицы, имела бы по меньшей мере степень 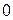 , а тогда степень фигурной скобки была бы не меньше
, а тогда степень фигурной скобки была бы не меньше 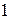 и, следовательно, степень всей правой части была бы не меньше
и, следовательно, степень всей правой части была бы не меньше 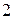 . Это, однако, невозможно, так как слева стоит
. Это, однако, невозможно, так как слева стоит  матрица степени
матрица степени 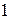 .
.
Таким образом,
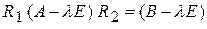 ,
,
откуда, приравнивая матричные коэффициенты при одинаковых степенях 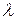 , получаем
, получаем
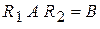 , (5)
, (5)
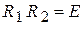 . (6)
. (6)
Равенство (6) показывает, что числовая матрица 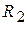 не только отлична от нуля, но даже является невырожденной, причем
не только отлична от нуля, но даже является невырожденной, причем
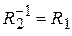 ,
,
а тогда равенство (5) принимает вид
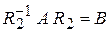 ,
,
что и доказывает подобие матриц 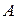 и
и 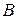 . □
. □
Пример 3. Являются ли следующие матрицы подобными
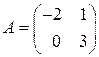 ,
, 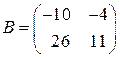 ?
?
Решение. Их характеристические матрицы эквивалентны, так как приводятся к одному и тому же каноническому виду
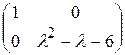 ,
,
поэтому матрицы 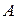 и
и 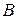 подобны.
подобны.