Распадающиеся квадратичные формы.
Перемножая любые две линейные формы от 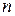 неизвестных,
неизвестных,
 ,
,
мы получим, очевидно, некоторую квадратичную форму. Не всякая квадратичная форма может быть представлена в виде произведения двух линейных форм, и мы хотим вывести условия, при которых это имеет место, т. е. при которых квадратичная форма является распадающейся.
ТЕОРЕМА Комплексная квадратичная форма  распадается тогда и только тогда, если ее ранг меньше или равен двум. Действительная квадратичная форма
распадается тогда и только тогда, если ее ранг меньше или равен двум. Действительная квадратичная форма  распадается тогда и только тогда, если или ее ранг не больше единицы, или же он равен двум, а сигнатура равна нулю.
распадается тогда и только тогда, если или ее ранг не больше единицы, или же он равен двум, а сигнатура равна нулю.
ДОКАЗАТЕЛЬСТВО. Рассмотрим сначала произведение линейных форм 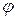 и
и  , т. е. таких форм, каждое слагаемое которых является первой степенью переменной с некоторым коэффициентом. Если хотя бы одна из этих форм нулевая, то их произведение будет квадратичной формой с нулевыми коэффициентами, т. е. оно имеет ранг 0. Если линейные формы
, т. е. таких форм, каждое слагаемое которых является первой степенью переменной с некоторым коэффициентом. Если хотя бы одна из этих форм нулевая, то их произведение будет квадратичной формой с нулевыми коэффициентами, т. е. оно имеет ранг 0. Если линейные формы 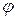 и
и  пропорциональны,
пропорциональны,
 ,
,
причем 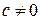 и форма
и форма 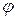 ненулевая, то пусть, например, коэффициент
ненулевая, то пусть, например, коэффициент  отличен от нуля. Тогда невырожденное линейное преобразование
отличен от нуля. Тогда невырожденное линейное преобразование
 при
при 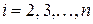
приводит квадратичную форму  к виду
к виду
 .
.
Справа стоит квадратичная форма ранга 1, а поэтому и квадратичная форма  имеет ранг 1. Если же, наконец, линейные формы
имеет ранг 1. Если же, наконец, линейные формы 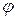 и
и  не являются пропорциональными, то пусть, например,
не являются пропорциональными, то пусть, например,
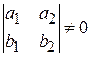 .
.
Тогда линейное преобразование

будет невырожденным; оно приводит квадратичную форму  к виду
к виду
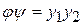 .
.
Справа стоит квадратичная форма ранга 2, имеющая в случае действительных коэффициентов сигнатуру 0.
Перейдем к доказательству обратного утверждения. Квадратичная форма ранга 0 может рассматриваться как произведение двух линейных форм, одна из которых нулевая. Далее, квадратичная форма  ранга 1 невырожденным линейным преобразованием приводится к виду
ранга 1 невырожденным линейным преобразованием приводится к виду
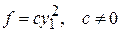 ,
,
т. е. к виду
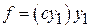 .
.
Выражая  линейно через
линейно через 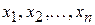 , мы получим представление формы
, мы получим представление формы 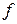 в виде произведения двух линейных форм. Наконец, действительная квадратичная форма
в виде произведения двух линейных форм. Наконец, действительная квадратичная форма  ранга 2 и сигнатуры 0 приводится невырожденным линейным преобразованием к виду
ранга 2 и сигнатуры 0 приводится невырожденным линейным преобразованием к виду
 ;
;
к этому же виду может быть приведена любая комплексная квадратичная форма ранга 2. Однако
 ,
,
но справа, после замены  и
и 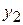 их линейными выражениями через
их линейными выражениями через 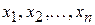 , будет стоять произведение двух линейных форм. □
, будет стоять произведение двух линейных форм. □