Вправи для повторення
258. Розв’яжіть рівняння:
а)5х - 3 = 3х + 17; б)7х + 32 = 12х + 25;
в) 2(х - 11) - 5(5 - 2х) = –23; г) 8(-3х + 4) + 14(3 + 2х) = 4 + 2х.
259.Футбольна команда у 15 матчах набрала 23 очка, програвши 6 матчів. У скількох матчах команда здобула перемогу і скільки матчів зіграла внічию? (За перемогу команді нараховується 3 очка, за нічию ¾ 1 очко, за поразку ¾ 0 очок.)
260.Середнє арифметичне трьох чисел дорівнює -8. Перше число на 5 більше від другого, а друге — на 1 менше від третього. Знайдіть ці числа.
8. Властивості степеня з натуральним показником
1. Множення степенів з однаковими основами.
Розглянемо добутки двох степенів з основою а. Врахувавши, що а1 = а, матимемо:
а1а1 = аa = а2 = а1 + 1; а2а1 = (аа)a = ааа = а3 = а2 + 1.
Отже, а1а1 = а1 + 1, а2а1 = а2 + 1. У цих прикладах добуток степенів з однаковими основами дорівнює степеню з тією ж основою і показником, який дорівнює сумі показників степенів. Таку властивість має добуток будь-яких степенів з однаковими основами.
| Властивість 1 | Для будь-якого числа а й довільних натуральних чисел m і n справджується рівність |
amаn = аm + n.
● Доведення. Врахувавши означення степеня, матимемо:
amаn = =
= = аm + n. ●
= аm + n. ●
Із властивості 1, яку ще називають основною властивістю степеня, випливає правило множення степенів:
Щоб перемножити степені з однаковими основами, потрібно основу залишити ту саму, а показники степенів додати.
Наприклад:
32 × 33 = 32 + 3 = 35; 24 × 2 = 24 × 21 = 24 + 1 = 25; b7 × b8 = b7 + 8 = b15.
Правило множення степенів поширюється на добуток трьох і більше степенів. Наприклад:
52 × 54 × 56 = 52 + 4 + 6 = 512; b5 × b3 × b7 × b = b5 + 3 + 7 + 1 = b16.
2. Ділення степенів з однаковими основами.
Розглянемо рівність а2а3 = а5, де а ¹ 0. Із цієї рівності за означенням
частки маємо: а5 : а3 = а2. Рівність а5 : а3 = а2 можна переписати так:
а5 : а3 = а5 - 3.
У цьому прикладі частка степенів з однаковими основами дорівнює степеню з тією ж основою й показником, який дорівнює різниці показника степеня діленого й показника степеня дільника. Сформулюємо й доведемо відповідну властивість у загальному випадку.
| Властивість 2 | Для будь-якого числа а ¹ 0 та довільних натуральних чисел m і n, де m > n, справджується рівність |
аm : аn = аm - n.
● Доведення. Оскільки am - n × аn = аm - n + n = аm, тобто am - n × аn = аm, то за означенням частки маємо: аm : аn = аm - n. ●
З доведеної властивості випливає правило ділення степенів:
Щоб поділити степені з однаковими основами, потрібно основу залишити ту саму, а від показника степеня діленого відняти показник степеня дільника.
Наприклад: 37 : 32 = 37 - 2 = 35; х4 : х = х4 : х1 = х4 - 1 = х3.
3. Піднесення степеня до степеня.
Піднесемо степінь а2 до куба:
(а2)3 = а2 × а2 × а2 = а2 + 2 + 2 = а2×3.
Отже, (а2)3 = а2×3. Із прикладу видно: щоб піднести квадрат числа до куба, потрібно залишити ту ж основу й узяти показник, який дорівнює добутку показників. Сформулюємо й доведемо відповідну властивість у загальному випадку.
| Властивість 3 | Для будь-якого числа а та довільних натуральних чисел m і n справджується рівність |
(am)n = аmn.
● Доведення.
(am)n = =
=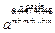 = аmn. ●
= аmn. ●
Із властивості 3 випливає правило піднесення степеня до степеня:
Щоб піднести степінь до степеня, потрібно основу залишити ту саму, а показники степенів перемножити.
Наприклад: (43)5 = 43 × 5 = 415; (b6)4 = b6 × 4 = b24.
4. Піднесення добутку до степеня.
Піднесемо добуток аb до куба:
(аb)3 = аb × аb × аb = (аaa) × (bbb) = а3b3.
Отже, (аb)3 = а3b3. Із прикладу видно: щоб піднести до куба добуток, потрібно піднести до куба кожний множник і результати перемножити.
Сформулюємо й доведемо відповідну властивість у загальному випадку.
| Властивість 4 | Для будь-яких чисел а та b і довільного натурального числа n справджується рівність |
(ab)n = аnbn.
● Доведення.
(ab)n =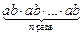 =
= ×
×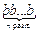 = аnbn. ●
= аnbn. ●
Маємо таке правило:
Щоб піднести до степеня добуток, досить піднести до цього степеня кожний множник і результати перемножити.
Це правило поширюється на добуток трьох і більше множників. Наприклад:
(5ab)3 = 53a3b3 = 125a3b3; (abху)n = anbnхnуn.
Зауваження.Доведені тотожності amаn = аm + n, аm : аn = аm - n, (am)n = аmn, (ab)n = аnbn, які виражають властивості степеня, дозволяють не тільки замінювати вирази, що стоять у їхніх лівих частинах, виразами, що стоять у правих частинах, а й навпаки:
am + n = аmаn; am - n = аm : аn; аmn = (am)n = (an)m; аnbn = (ab)n.
 Приклади розв’язання вправ
Приклади розв’язання вправ
Приклад 1. Спростити вираз (a2а)3 × (a3а2)2.
● (a2а)3 × (a3а2)2 = (a3)3 × (a5)2 = а9a10 = a19. ●
Приклад 2. Обчислити:
а) 0,36 : 0,34 + 0,14 : 0,1; б)2,55× 26× 0,45.
● а)0,36 : 0,34 + 0,14 : 0,1 = 0,32 + 0,13 = 0,09 + 0,001 = 0,091;
б)2,55× 26× 0,45 = (2,55× 0,45) × 26 = (2,5× 0,4)5× 26 = 15× 26 = 64. ●
Приклад 3. Подати 418 у вигляді степеня з основою 42; 43; 46; 49.
● 418 = 42 × 9 = (42)9; 418 = (43)6; 418 = (46)3; 418 = (49)2. ●
Приклад 4. Подати у вигляді степеня добуток а6b6.
● а6b6 = (аb)6. ●