Свойства операций над векторами.
Итак, мы определили операцию сложения векторов и операцию умножения вектора на число. При этом для любых векторов 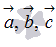 и произвольных действительных чисел
и произвольных действительных чисел 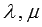 можно при помощи геометрических построений обосновать следующие свойства операций над векторами. Некоторые из них очевидны.
можно при помощи геометрических построений обосновать следующие свойства операций над векторами. Некоторые из них очевидны.
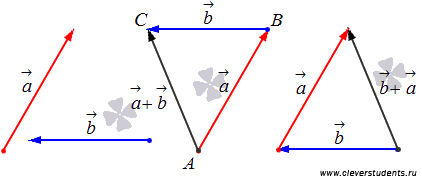
1. Свойство коммутативности  .
.
2. Свойство ассоциативности сложения  .
.
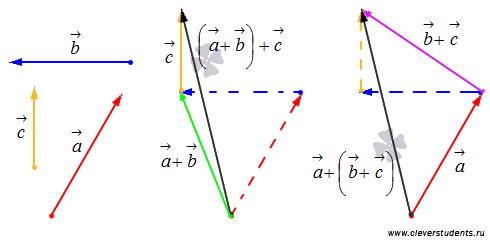
3. Существует нейтральный элемент по сложению, которым является нулевой вектор  , и
, и 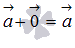 . Это свойство очевидно.
. Это свойство очевидно.
4. Для любого ненулевого вектора 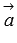 существует противоположный вектор
существует противоположный вектор  и верно равенство
и верно равенство 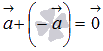 . Это свойство очевидно без иллюстрации.
. Это свойство очевидно без иллюстрации.
5. Сочетательное свойство умножения 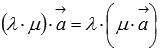 . К примеру, растяжение вектора в 6 раз можно произвести, если сначала его растянуть вдвое и полученный вектор растянуть еще втрое. Аналогичного результата можно добиться, например, сжав вектор вдвое, а полученный вектор растянуть в 12 раз.
. К примеру, растяжение вектора в 6 раз можно произвести, если сначала его растянуть вдвое и полученный вектор растянуть еще втрое. Аналогичного результата можно добиться, например, сжав вектор вдвое, а полученный вектор растянуть в 12 раз.
6. Первое распределительное свойство 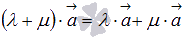 . Это свойство достаточно очевидно.
. Это свойство достаточно очевидно.
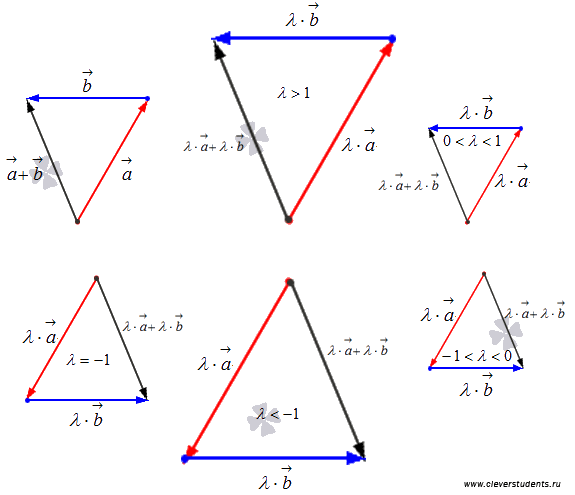
7. Второе распределительное свойство 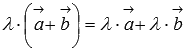 . Это свойство справедливо в силу подобия треугольников, изображенных ниже.
. Это свойство справедливо в силу подобия треугольников, изображенных ниже.
8. Нейтральным числом по умножению является единица, то есть, 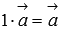 . При умножении вектора на единицу с ним не производится никаких геометрических преобразований.
. При умножении вектора на единицу с ним не производится никаких геометрических преобразований.
Рассмотренные свойства дают нам возможность преобразовывать векторные выражения.
Свойства коммутативности и ассоциативности операции сложения векторов позволяют складывать векторы в произвольном порядке.
Операции вычитания векторов как таковой нет, так как разность векторов 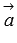 и
и  есть сумма векторов
есть сумма векторов 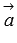 и
и 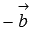 .
.
Учитывая рассмотренные свойства операций над векторами, мы можем в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования так же как и в числовых выражениях.