Билинейные формы

Пусть L_n – n-мерное линейное пространство над полем Р .

Определение 59. Отображение f : (L_n ´ L_n ) ® Р называется билинейной формой (или билинейной функцией), заданной на L_n , если для любых векторов а, в, с и любого элемента aÎ Р выполняются условия:

f (а + в, с) = f (а, с) + f (в, с) ; f (а, в + с ) = f (а, в) + f (а, с); f (a×а) = a×f(а).

(Иными словами, билинейная форма линейна по обоим переменным.)

Пусть в L_n зафиксирован базис е = (е₁, е₂,... , е_n), а = х₁е₁ + х₂е₂ + … + х_nе_n,

в = у₁е₁ + у₂е₂ + … + у_nе_n, f (е_к , е_р) = a_кр . Тогда из определения 58 следует

f (а, в) = f (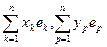) = = 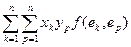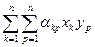, где a_кр – элементы поля Р.

Итак, f (а, в) = 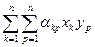(55) – запись билинейной формы в координатах.

Матрица А =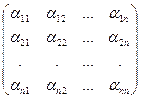

называется матрицей данной билинейной формы. Если х и у – столбцы координат векторов а и в, то билинейную форму можно записать в матричном виде: f (а, в) = хТ× А × у (56)

Если е¹ = (е₁¹, е₂¹,... , е_n¹) – другой базис в L_n и Т – матрица перехода от базиса е к базису е¹, то столбцы координат векторов а и в в этих базисах связаны формулами х = Т×х¹, у =Т×у¹. Подставив в формулу (56), получим f (а, в) = (Тх¹)^Т× А × (Ту¹) = (х¹)^Т×(Т^Т×А×Т)×у¹. Следовательно, матрицы билинейной формы в разных базисах связаны формулой

А¹ = Т^Т×А×Т (57)

Определение 60. Билинейная форма называется симметрической, если

f (а, в) = f ( в, а) для любых векторов а и в. (57)

Очевидно, верно следующее утверждение:

Теорема 62. Билинейная форма является симметрической тогда и только тогда, когда она в любом базисе имеет симметрическую матрицу.

Теорема 63. В любом базисе евклидова пространства Е_n скалярное произведение векторов задаётся симметрической билинейной формой.

Доказательство. По формуле (42) скалярное произведение векторов а и в равно

(а, в)= х ^Т×Г×у. Матрица Г – симметрическая, поэтому, согласно формуле (56), скалярное произведение задано симметрической билинейной формой.