Комплексные числа
Определение 4. Комплексным числом называется выражение вида а + вi, где а и в – действительные числа, i2 = -1 (i называют мнимой единицей).
Если z = а + вi, то а называется действительной частью числа z, а вi – его мнимой частью. Говорят, что комплексное число задано в алгебраической форме. Во множестве комплексных чисел вводятся операции сложения и умножения следующим образом. Если z = а + вi и z1 = а1 + в1i два комплексных числа, то
z + z1 = (а + а1) + (в + в1)×i, z×z1 = (аа1 - вв1) + (ав1 + а1в)×i.
Эти операции обладают следующими свойствами.
1. Сложение и умножение для любой пары комплексных чисел определено и однозначно.
2. z + z1 = z1 + z, z × z1 = z1× z для любых z и z1 (коммутативный закон сложения и умножения).
3. z + (z1 + z2) = (z + z1) + z2, z ×(z1 × z2) = (z × z1) × z2 для любых z, z1 и z2 (ассоциативный закон сложения и умножения).
4. z × (z1 + z2) = z ×z1 + z× z2 для любых z, z1 и z2 (дистрибутивный закон).
5. Если 0 = 0 + 0×i, то z + 0 = z для любого z.
6. Если -z = -а + (-в)i, то z + (-z) = 0, т.е. для любого комплексного числа существует противоположное число.
Число  = а - вi называется сопряжённым для числа z, z +
= а - вi называется сопряжённым для числа z, z +  = 2а, z×
= 2а, z× = а2 + в2. Следовательно, если z ¹ 0, то z×
= а2 + в2. Следовательно, если z ¹ 0, то z× ¹ 0.
¹ 0.
7. Если 1 = 1 + 0×i, то 1×z = z.
8. Если z ¹ 0 и  , то
, то 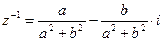 . Следовательно, для каждого отличного от нуля комплексного числа существует обратное число.
. Следовательно, для каждого отличного от нуля комплексного числа существует обратное число.
Итак, во множестве комплексных чисел введены такие же операции (сложение и умножение), как и во множествах рациональных и действительных чисел. И свойства этих операций во всех трёх множествах одинаковы. Такие множества называются полями. Их общее обозначение Р. Конкретные обозначения: Q – поле рациональных чисел, R – поле действительных чисел, С – поле комплексных чисел.
Зафиксируем на евклидовой плоскости прямоугольную систему координат. Пусть
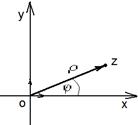
| z = а + bi. Будем говорить, что точка с координатами (а, b)и вектор с этими же координатами изображаютданное комплексное число. Длину вектора 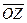 назовём модулем числа z, Угол (ориентированный) между осью (ОХ) и этим вектором назовём аргументом данного числа. Очевидно, каждое комплексное число имеет бесконечно много значений аргумента. Так как а = пр(ОХ) назовём модулем числа z, Угол (ориентированный) между осью (ОХ) и этим вектором назовём аргументом данного числа. Очевидно, каждое комплексное число имеет бесконечно много значений аргумента. Так как а = пр(ОХ)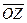 и b = пр(ОУ) и b = пр(ОУ)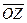 , то а = r×cosj, , то а = r×cosj,
|
b = r×sinj, r2 = а2 + b2, tgj = 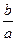 . Подставив значения а и b в алгебраическую форму числа z, получим z = r (cosj + i×sinj). Это тригонометрическая форма комплексного числа. Легко проверить, что z × z1 = r×r1(cos(j + j1) + sin(j + j1));
. Подставив значения а и b в алгебраическую форму числа z, получим z = r (cosj + i×sinj). Это тригонометрическая форма комплексного числа. Легко проверить, что z × z1 = r×r1(cos(j + j1) + sin(j + j1)); 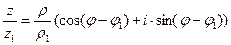 , если z1 ¹ 0. Отсюда zn = rn (cosnj + i×sinnj). Можно показать, что
, если z1 ¹ 0. Отсюда zn = rn (cosnj + i×sinnj). Можно показать, что
 , где к = 1, 2, … , n и
, где к = 1, 2, … , n и 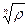 - арифметическое значение корня из действительного числа r. Таким образом, корень n-ой степени из комплексного числа имеет n различных значений.
- арифметическое значение корня из действительного числа r. Таким образом, корень n-ой степени из комплексного числа имеет n различных значений.