Внутренняя прямая сумма

Определение 2. Пространство 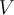называется прямой суммой²⁾ своих векторных подпространств 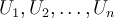, если каждый вектор 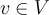может быть представлен одним и только одним способом в виде суммы

где .

Прямая сумма векторных пространств обозначается через .

Замечание 2. Определенная таким образом прямая сумма называется внутренней.

Пример 2. Пусть 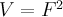и подпространства и определены также, как в примере 1. Тогда сумма 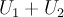является прямой, то есть .

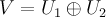Предложение 3. Сумма является прямой тогда и только тогда, когда выполнено любое из следующих двух условий:

1. 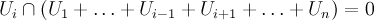для ,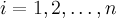

2. .

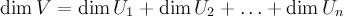Следствие 1. Если , то сумма является прямой тогда и только тогда, когда .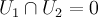

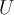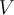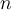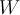Предложение 4. Для любого -мерного подпространства векторного пространства размерности найдется такое -мерное подпространство , что .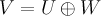

Определение 3. Для подпространства 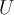векторного пространства 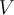подпространство 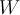из предложения 4, то есть такое, что 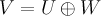, называется дополнительным подпространством³⁾ к .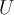