Собственные вектора и собственные значения
Определение 2. Ненулевой вектор из одномерного подпространства, инвариантного относительно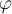 
, называется собственным вектором2) оператора 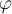. Таким образом, собственный вектор 
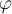оператора удовлетворяет условию 
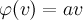. При этом скаляр 
называется собственным значением3) оператора .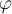
Пример 1. Пусть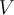 
— двумерное векторное пространство над полем действительных чисел 
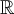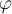, и — линейный оператор на 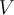, имеющий в некотором базисе 
матрицу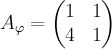 
. Тогда вектор 
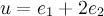является собственным вектором оператора 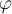с собственным значением 
, а вектор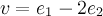 
— собственным вектором с собственным значением
. В этом можно удостовериться, решив уравнения,
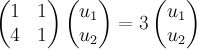и 
.
Определение 3. Подпространство4)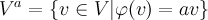 
называется собственным подпространством5) оператора 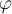. Размерность 
называется геометрической кратностью6) собственного значения 
.
Определение 4. Множество всех собственных значений линейного оператора 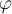называется спектром7) этого оператора и обозначается символом 
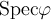. Точка спектра называется простой8), если ей соответствует геометрическая кратность 1. Спектр называется простым9), если каждая точка спектра проста.
Предложение 1. Собственные векторы, принадлежащие различным собственным значениям, линейно независимы. Сумма 
является прямой.
Пример 2. Опишем спектр линейного оператора 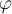на векторном пространстве 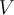из примера 1. Так как на двумерном векторном пространстве любой линейный оператор имеет не более двух собственных значений10), то из примера 1 видно, что и образуют простой спектр этого оператора.