Базис и размерность пространства
Так как в линейном пространстве векторы можно складывать и умножать на числа, то из них можно составлять линейные комбинации и можно ввести понятия линейной зависимости и линейной независимости системы векторов так же, как это было сделано в разделе "Линейная зависимость векторов". На случай произвольного линейного пространства определения 10.14 и 10.15 переносятся дословно. Предложения 10.6, 10.7, 10.8 переносятся дословно вместе с доказательствами.
На основе линейной зависимости в линейном пространстве вводится определение базиса. Оно почти дословно совпадает с определением 10.16.
Определение 18.2 Базисом линейного пространства  называется такая конечная упорядоченная линейно независимая система векторов, что любой вектор пространства
называется такая конечная упорядоченная линейно независимая система векторов, что любой вектор пространства  является линейной комбинацией этих векторов.
является линейной комбинацией этих векторов.
В отличие от трехмерного пространства векторов, в некоторых линейных пространствах базис не существует.
Пример 18.2 Пусть  -- линейное пространство всех многочленов с веществеными коэффициентами. Покажем, что в этом пространстве базис не существует.
-- линейное пространство всех многочленов с веществеными коэффициентами. Покажем, что в этом пространстве базис не существует.
Предположим противное. Пусть векторы  образуют в этом пространстве базис.
образуют в этом пространстве базис.
Каждый вектор пространства  -- это многочлен. Пусть
-- это многочлен. Пусть

| |

| |

| |
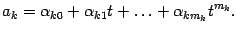
|
Из степеней многочленов 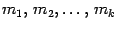 выберем наибольшую и обозначим ее буквой
выберем наибольшую и обозначим ее буквой  . Возьмем многочлен
. Возьмем многочлен 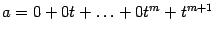 . Так как
. Так как  и векторы
и векторы  образуют базис, то
образуют базис, то 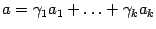 , где
, где  -- вещественные числа. Следовательно,
-- вещественные числа. Следовательно,  является суммой многочленов степеней меньших, чем
является суммой многочленов степеней меньших, чем  , и поэтому его степень должна быть меньше, чем
, и поэтому его степень должна быть меньше, чем  . С другой стороны, по определению, многочлен
. С другой стороны, по определению, многочлен  имеет степень
имеет степень  . Получили противоречие. Значит, предположение о существовании базиса неверно.
. Получили противоречие. Значит, предположение о существовании базиса неверно.
Теорема 18.1 В линейном пространстве любые два базиса содержат одинаковое число векторов.
Доказательство теоремы мы приводить не будем. Желающие могут найти его в любом учебнике по линейной алгебре, например в [1].
Определение 18.3 Линейное пространство  , в котором существует базис, состоящий из
, в котором существует базис, состоящий из  векторов, называется
векторов, называется  -мерным линейным или векторным пространством. Число
-мерным линейным или векторным пространством. Число  называется размерностью пространства и обозначается
называется размерностью пространства и обозначается 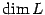 . Линейное пространство, в котором не существует базис, называетсябесконечномерным.
. Линейное пространство, в котором не существует базис, называетсябесконечномерным.
Примером бесконечномерного пространства является пространство всех многочленов с вещественными коэффициентами. Как показано в примере 18.2 в этом пространстве базис отсутствует.
Предложение 18.1 Пространство столбцов из  элементов, являющихся вещественными числами, имеет рамерность
элементов, являющихся вещественными числами, имеет рамерность  .
.
Доказательство. Возьмем систему векторов
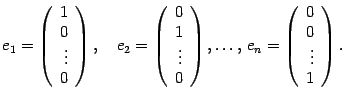
Покажем, что эта система линейно независима. Составим линейную комбинацию и приравняем ее к нулю:

Преобразуем левую часть:
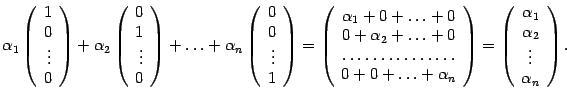
Следовательно,

откуда  ,
,  ,
, 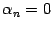 . Итак, система векторов
. Итак, система векторов 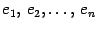 -- линейно независима.
-- линейно независима.
Пусть 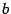 -- произвольный вектор пространства,
-- произвольный вектор пространства,  Очевидно, что
Очевидно, что

Следовательно, вектор 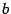 является линейной комбинацией векторов
является линейной комбинацией векторов 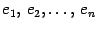 . Тем самым доказано, что векторы
. Тем самым доказано, что векторы 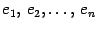 образуют базис в пространстве столбцов из
образуют базис в пространстве столбцов из  элементов. Размерность пространства равна числу векторов в базисе. Следовательно, пространство --
элементов. Размерность пространства равна числу векторов в базисе. Следовательно, пространство --  -мерное.
-мерное.
Пространство столбцов из  элементов, являющихся вещественными числами, обозначается
элементов, являющихся вещественными числами, обозначается  .
.
Предложение 18.2 Пространство столбцов из  элементов, являющихся комплексными числами, имеет размерность
элементов, являющихся комплексными числами, имеет размерность  .
.
Доказательство такое же, как и в предыдущем предложении. Это пространство обозначается 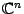 .
.
Пример 18.3 Пространство решений однородной системы линейных уравнений 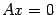 имеет базис из
имеет базис из  решений, где
решений, где  -- число неизвестных, а
-- число неизвестных, а 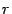 -- ранг матрицы
-- ранг матрицы 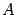 . Этим базисом служит фундаментальная система решений (см. определение 15.5 и теорему 15.3).
. Этим базисом служит фундаментальная система решений (см. определение 15.5 и теорему 15.3).
| 01.Образ и ядро линейного оператора. Ранг и дефект линейного оператора | 
| 
| 
|
Пусть 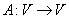 - линейный оператор действующий в линейном пространстве V (комплексном или вещественном)
Определение: Совокупность всевозможных векторов вида - линейный оператор действующий в линейном пространстве V (комплексном или вещественном)
Определение: Совокупность всевозможных векторов вида  называется образом оператора A и обозначается ImA. Таким образом называется образом оператора A и обозначается ImA. Таким образом  .
Определение: Совокупность всевозможных векторов .
Определение: Совокупность всевозможных векторов  для которых для которых  называется ядром оператора A и обозначается KerA. Таким образом называется ядром оператора A и обозначается KerA. Таким образом 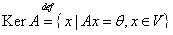 .
Утверждение: образ и ядро линейного оператора А являются подпространствами линейного пространства V.
Доказательство: В самом деле в силу линейности оператора А имеем:
1) .
Утверждение: образ и ядро линейного оператора А являются подпространствами линейного пространства V.
Доказательство: В самом деле в силу линейности оператора А имеем:
1)  тогда тогда 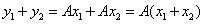 и т. к и т. к  то то 
 и т. к. и т. к.  , то , то 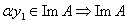 является подпространством пространства V.
2) является подпространством пространства V.
2)  отсюда отсюда  . .
 является подпространством пространства V. #
Пример:
Пусть V – n мерное комплексное или вещественное линейное пространство.
1) Тождественный оператор является подпространством пространства V. #
Пример:
Пусть V – n мерное комплексное или вещественное линейное пространство.
1) Тождественный оператор  , при этом Ax = Ix = X, тогда ImA=ImI=V, KerA=KerI={θ}
/ ядро состоит из единственного нулевого элемента / , при этом Ax = Ix = X, тогда ImA=ImI=V, KerA=KerI={θ}
/ ядро состоит из единственного нулевого элемента /  2) Нулевой оператор
2) Нулевой оператор , тогда , тогда 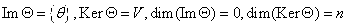 3) Рассмотрим оператор дифференцирования
3) Рассмотрим оператор дифференцирования 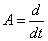 на пространстве на пространстве  многочленов степени не выше N, тогда многочленов степени не выше N, тогда 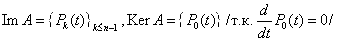 отсюда отсюда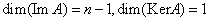 . Видно, что во всех приведенных примерах справедливо: . Видно, что во всех приведенных примерах справедливо:
 , что не является случайным.
Теорема (о сумме размерностей образа и ядра линейного оператора) :
Пусть A - линейный оператор, действующий в линейном пространстве V. Тогда сумма размерностей образа и ядра оператора равна размерности данного линейного пространства, т. е. , что не является случайным.
Теорема (о сумме размерностей образа и ядра линейного оператора) :
Пусть A - линейный оператор, действующий в линейном пространстве V. Тогда сумма размерностей образа и ядра оператора равна размерности данного линейного пространства, т. е.  Доказательство:
Пусть
Доказательство:
Пусть 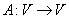 , причем , причем 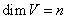 Выберем в пространстве V произвольный базис
Выберем в пространстве V произвольный базис  . Поскольку по определению . Поскольку по определению 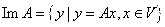 , то можно записать, что , то можно записать, что 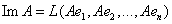 линейная оболочка, порождаемая совокупностью образов базисных векторов линейная оболочка, порождаемая совокупностью образов базисных векторов 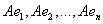 , причем , причем  , где R – максимальное число л. н.з. векторов в системе , где R – максимальное число л. н.з. векторов в системе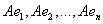 . Но координаты именно этих векторов стоят в столбцах матрицы . Но координаты именно этих векторов стоят в столбцах матрицы 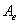 линейного оператора А в базисе линейного оператора А в базисе , поэтому , поэтому  .
Рассмотрим ядро оператора А: .
Рассмотрим ядро оператора А: 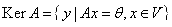 .
В выбранном базисе равенству .
В выбранном базисе равенству  соответствует однородная СЛАУ: соответствует однородная СЛАУ: , которая, как известно, имеет (N-R) л. н.з. решений, образующих ФСР. Поскольку неизвестными данной системы являются координаты векторов, составляющих KerA, то отсюда заключаем, что dim(KerA)=N-R. В результате получаем, что , которая, как известно, имеет (N-R) л. н.з. решений, образующих ФСР. Поскольку неизвестными данной системы являются координаты векторов, составляющих KerA, то отсюда заключаем, что dim(KerA)=N-R. В результате получаем, что 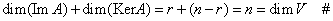 Определение: Размерность образа оператора называется рангом оператора, размерность ядра оператора называется дефектом оператора.
Определение: Линейный оператор
Определение: Размерность образа оператора называется рангом оператора, размерность ядра оператора называется дефектом оператора.
Определение: Линейный оператор 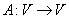 называется невырожденным, если в произвольном базисе (E) данного линейного пространства V Оператор А имеет невырожденную матрицу называется невырожденным, если в произвольном базисе (E) данного линейного пространства V Оператор А имеет невырожденную матрицу 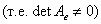 .
Следствие: Если А – невырожденный линейный оператор, то его образ совпадает со всем пространством, в котором этот оператор действует.
Доказательство: Если .
Следствие: Если А – невырожденный линейный оператор, то его образ совпадает со всем пространством, в котором этот оператор действует.
Доказательство: Если 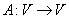 , то по предыдущей теореме запишем , то по предыдущей теореме запишем 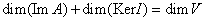 . ПоСвойству 40 невырожденных операторов (докажем позже в параграфе 12 главе 7) равенство . ПоСвойству 40 невырожденных операторов (докажем позже в параграфе 12 главе 7) равенство  возможно только при возможно только при  отсюда отсюда  откуда откуда 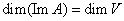 . Т. к. . Т. к. 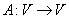 , то отсюда следует, что , то отсюда следует, что 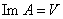 .
Определение: Подпространство L пространства V называется инвариантным относительно линейного оператора А, если .
Определение: Подпространство L пространства V называется инвариантным относительно линейного оператора А, если 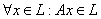 .
Теорема (об инвариантности образа и ядра линейного оператора):
Образ и ядро линейного оператора А являются подпространствами инвариантными относительно оператора А.
Доказательство:
1) Пусть .
Теорема (об инвариантности образа и ядра линейного оператора):
Образ и ядро линейного оператора А являются подпространствами инвариантными относительно оператора А.
Доказательство:
1) Пусть 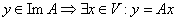 , т. к. , т. к. 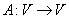 то то  и поэтому и поэтому  , т. е. подпространство ImA является инвариантным относительно оператора А.
2) Пусть , т. е. подпространство ImA является инвариантным относительно оператора А.
2) Пусть  . Тогда . Тогда , т. у. , т. у. 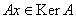 а значит подпространство KerA инвариантно относительно оператора А. а значит подпространство KerA инвариантно относительно оператора А.
|
Линейный оператор 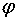 векторного пространства V задан матрицей А в некотором базисе
векторного пространства V задан матрицей А в некотором базисе 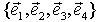 . Найдите ядро и дефект линейного оператора
. Найдите ядро и дефект линейного оператора 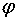 , если
, если
