Система випадкових величин.
2. Закон розподілу двохвимірної ДВВ.
3. Функції розподілу двохвимірної ВВ. Залежність та незалежність ВВ.
4. Числові характеристики двохвимірної ВВ.
5. Функції ВВ та їх характеристики.
Раніше розглядались ВВ, які при кожному випробуванні визначались одним можливим значенням. Тому таку ВВ називають одновимірною.
Якщо можливі значення ВВ визначаються у кожному випробуванні  числами, то такі ВВ називають відповідно двох-, трьох-,...,
числами, то такі ВВ називають відповідно двох-, трьох-,...,  -вимірними. Двохвимірну ВВ будемо позначати
-вимірними. Двохвимірну ВВ будемо позначати 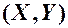 , де
, де  та
та 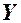 - компоненти. ВВ
- компоненти. ВВ  та
та 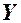 , що розглядаються одночасно, утворюють систему двох випадкових величин. Аналогічно можна розглядати систему
, що розглядаються одночасно, утворюють систему двох випадкових величин. Аналогічно можна розглядати систему  ВВ.
ВВ.
Означення. Сукупність  одночасно розглядаємих ВВ
одночасно розглядаємих ВВ  називають системою ВВ.
називають системою ВВ.
Систему  ВВ
ВВ  можна розглядати як випадкову точку в
можна розглядати як випадкову точку в  -вимірному просторі з координатами
-вимірному просторі з координатами  або як випадковий вектор, напрямлений з початку координат у точку
або як випадковий вектор, напрямлений з початку координат у точку  .
.
При 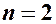 дістаємо систему двох ВВ
дістаємо систему двох ВВ 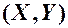 , яку можна інтерпретувати як випадкову точку
, яку можна інтерпретувати як випадкову точку  на площині
на площині  або як випадковий вектор
або як випадковий вектор 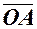 :
:
Багатовимірні ВВ можуть бути дискретними - ДВВ або неперервними –НВВ (компоненти цих величин відповідно будуть дискретними або неперервними).
Означення. Законом розподілу двохвимірної ДВВ називають сукупність із множини її можливих значень  та їх імовірностей
та їх імовірностей  .
.
Найчастіше закон розподілу двохвимірної ДВВ задають таблицею:

| 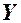
| |||||
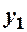
| 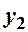
| ... | 
| ... | 
| |
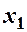
| 
| 
| ... | 
| ... | 
|
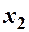
| 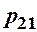
| 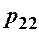
| ... | 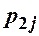
| ... | 
|
| ... | ... | ... | ... | ... | ... | ... |

| 
| 
| ... | 
| ... | 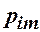
|
| ... | ... | ... | ... | ... | ... | ... |

| 
| 
| ... | 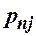
| ... | 
|
Події  .,
.,  утворюють повну группу, тому сума імовірностей таблиці дорівнює одиниці, тобто виконується умова нормування:
утворюють повну группу, тому сума імовірностей таблиці дорівнює одиниці, тобто виконується умова нормування:
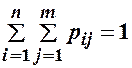 .
.
Закон розподілу двохвимірної ДВВ дозволяє отримати закони розподілу кожної компоненти. Відповідні імовірності для можливих значень компонент знаходяться сумуванням імовірностей у рядках та стовпцях таблиці.
Приклад 7.1. Знайти закони розподілу компонент двохвимірної ВВ, закон розподілу якої заданий таблицею:

| 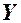
| |
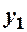
| 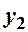
| |

| 0,1 | 0,06 |

| 0,3 | 0,18 |
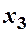
| 0,2 | 0,16 |
Розв’язування:
Означення. Інтегральною функцією розподілу (функцією розподілу) двохвимірної ВВ 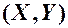 називають функцію двох змінних
називають функцію двох змінних 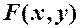 , яка визначає для кожної пари
, яка визначає для кожної пари 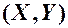 імовірність виконання нерівностей
імовірність виконання нерівностей 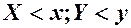 , тобто
, тобто
 .
.
Геометричний сенсфункції розподілу 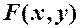 - це імовірність того, що випадкова точка
- це імовірність того, що випадкова точка 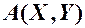 попаде у нескінченний прямокутник з вершиною в точці
попаде у нескінченний прямокутник з вершиною в точці  :
:
Неважко переконатись у наступних властивостях функції розподілу:
1)  , причому
, причому 
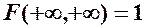 .
.
2) 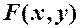 - неспадна функція за кожним аргументом, тобто
- неспадна функція за кожним аргументом, тобто
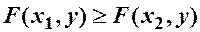 ,якщо
,якщо  ;
;
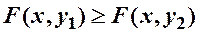 ,якщо
,якщо 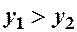 .
.
3) Імовірність попадання випадкової точки до прямокутника  можна знайти за формулою:
можна знайти за формулою:

Зауважимо, що інтегральна функція розподілу ДВВ – розривна (кусочно-стала), а у неперервних ВВ – неперервна. НВВ можна задавати також щільністю імовірностей.
Означення. Диференціальною функцією розподілу (двохвимірною щільністю імовірностей)  двохвимірної НВВ
двохвимірної НВВ 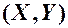 називають мішану частинну похідну другого порядку від інтегральної функції розподілу
називають мішану частинну похідну другого порядку від інтегральної функції розподілу
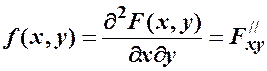 .
.
Щільність розподілу імовірностей  задовольняє властивостям:
задовольняє властивостям:
1) Вона невід’ємна, тобто  (як похідна неспадної функції).
(як похідна неспадної функції).
2)  (умова нормування).
(умова нормування).
3)  (зв’язок із інтегральною функцією).
(зв’язок із інтегральною функцією).
4) Імовірність попадання випадкової точки 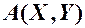 в область
в область  знаходиться за формулою
знаходиться за формулою  .
.
Дві випадкові величини незалежні, якщо закон розподілу однієї з них не залежить від того, які можливі значення прийняла інша величина. У супротивному випадку випадкові величини залежні.
Теорема. Для того, щоб ВВ  та
та 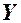 були незалежними, необхідно і достатньо, щоб інтегральна (або диференціальна) функція системи
були незалежними, необхідно і достатньо, щоб інтегральна (або диференціальна) функція системи 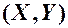 дорівнювала добутку інтегральних (диференціальних) функцій компонент
дорівнювала добутку інтегральних (диференціальних) функцій компонент
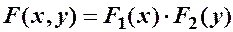 (або
(або  ).
).
Наслідок. Для незалежності двох ДВВ необхідно і достатньо, щоб  .
.
Числові характеристики двохвимірної ВВ.
Математичне сподівання двохвимірної (системи) ВВ 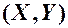 позначається
позначається  характеризує координати центру розподілуВВ. Ці координати у випадку НВВ знаходяться за формулами:
характеризує координати центру розподілуВВ. Ці координати у випадку НВВ знаходяться за формулами:

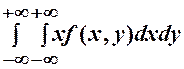 ,
,

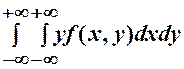 .
.
Дисперсії 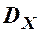 та
та 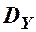 характеризують розсіювання випадкової точки
характеризують розсіювання випадкової точки 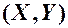 від центру розподілу
від центру розподілу  вздовж координатних осей Ох та Оу відповідно. Їх можна знаходити за формулами:
вздовж координатних осей Ох та Оу відповідно. Їх можна знаходити за формулами:
 ,
,
 .
.
Для опису двохвимірної ВВ крім математичного сподівання, дисперсії та середніх квадратичних відхилень  використовують також кореляційний момент (коваріацію):
використовують також кореляційний момент (коваріацію):
 .
.
Для НВВ:
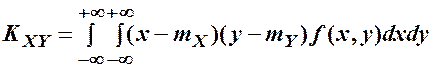 .
.
Для кількісної характеристики залежності ВВ часто використовують (особливо у статистиці) коефіцієнт кореляції:
 .
.
Якщо ВВ  та
та 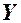 дискретні, то у вищенаведених формулах знаки інтегралів замінюють знаками суми по усім можливим значенням ВВ.
дискретні, то у вищенаведених формулах знаки інтегралів замінюють знаками суми по усім можливим значенням ВВ.
Означення. ВВ  та
та 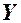 називають некорельованими, якщо їх кореляційний момент або коефіцієнт кореляції дорівнює нулю.
називають некорельованими, якщо їх кореляційний момент або коефіцієнт кореляції дорівнює нулю.
Властивості коефіцієнта кореляції.
1)  ;
;
2) якщо  та
та 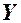 незалежні, то
незалежні, то  ;
;
3) якщо між  та
та 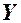 є лінійна залежність
є лінійна залежність 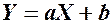 , де
, де  - постійні, то
- постійні, то 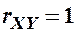 .
.
Зауваження. Якщо кореляційний момент або коефіцієнт кореляції відмінний від нуля, то ВВ  та
та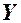 - корельовані. Дві корельовані ВВ обов’язково залежні. Але залежні ВВ можуть бути як корельованими, так і некорельованими, тобто їх коефіцієнт кореляції може бути відмінним від нуля або рівним нулю. Із незалежності ВВ випливає їх некорельованість, але із некорельованості не випливає незалежність ВВ. У випадку нормально розподілених ВВ із некорельованості випливає незалежність ВВ.
- корельовані. Дві корельовані ВВ обов’язково залежні. Але залежні ВВ можуть бути як корельованими, так і некорельованими, тобто їх коефіцієнт кореляції може бути відмінним від нуля або рівним нулю. Із незалежності ВВ випливає їх некорельованість, але із некорельованості не випливає незалежність ВВ. У випадку нормально розподілених ВВ із некорельованості випливає незалежність ВВ.
Функції ВВ та їх характеристики.
Означення. Якщо вказано закон (або правило) 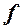 , за яким кожному можливому значенню ВВ
, за яким кожному можливому значенню ВВ  відповідає певне значення ВВ
відповідає певне значення ВВ 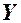 , то
, то 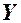 називають функцією
називають функцією  і позначають
і позначають  .
.
Відзначимо, що іноді різним можливим значенням ВВ  відповідають однакові значення ВВ
відповідають однакові значення ВВ 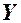 . Наприклад, якщо
. Наприклад, якщо 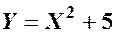 , то значенням
, то значенням 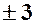 ВВ
ВВ  відповідає одне значення ВВ
відповідає одне значення ВВ 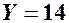 .
.
Однією із задач теорії імовірностей є визначення законів розподілу та числових характеристик функцій випадкового аргументу, закон розподілу якого відомий.
Нехай  , а аргумент
, а аргумент  - ДВВ, наприклад, задана таблицею
- ДВВ, наприклад, задана таблицею

| 
| 
| ... | 
|
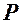
| 
| 
| ... | 
|
Тоді  також є ДВВ, закон розподілу якої буде мати вигляд:
також є ДВВ, закон розподілу якої буде мати вигляд:
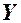
| 
| 
| ... | 
|
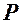
| 
| 
| ... | 
|
Математичне сподівання, дисперсію, середнє квадратичне відхилення та початкові і центральні моменти розподілу знаходять за формулами:
 ;
;
 ;
;
 ;
;
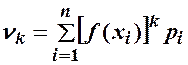 ;
;
 .
.
Приклад 7.2. ДВВ  задана таблицею
задана таблицею

| 
| 
| 
|
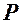
| 
| 
| 
|
Знайти закон розподілу та числові характеристики функції 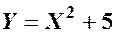 .
.
Розв’язування.
Нехай  - НВВ, закон розподілу якої заданий диференціальною функцією (щільністю розподілу імовірностей)
- НВВ, закон розподілу якої заданий диференціальною функцією (щільністю розподілу імовірностей)  , а ВВ
, а ВВ  . Якщо
. Якщо 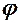 - диференційовна функція, монотонна на усьому проміжку можливих значень
- диференційовна функція, монотонна на усьому проміжку можливих значень  , то щільність розподілу функції
, то щільність розподілу функції  визначається за формулою:
визначається за формулою:
 , (*)
, (*)
де  - функція, обернена до функції
- функція, обернена до функції  .
.
Якщо  немонотонна функція на області визначення аргумента
немонотонна функція на області визначення аргумента  , то обернена функція неоднозначна, тому щільність розподілу
, то обернена функція неоднозначна, тому щільність розподілу 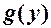 визначається як сума доданків, кількість яких дорівнює кількості значень оберненої функції:
визначається як сума доданків, кількість яких дорівнює кількості значень оберненої функції:
 , (**)
, (**)
де 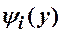 - обернені функції при заданому
- обернені функції при заданому  .
.
Алгоритм знаходження щільності розподілу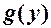 .
.
1. Визначити множину можливих значень для  .
.
2. Із функціональної залежності  знайти явний вираз
знайти явний вираз  через
через 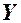 , тобто функцію
, тобто функцію  , обернену до функції
, обернену до функції  .
.
3. Знайти похідну  .
.
4. За формулою (*) записати щільність розподілу ВВ 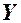 .
.
5. Перевірити умову нормування для 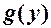 :
:  .
.
Приклад 7.3. ВВ  розподілена за нормальним законом з математичним сподіванням
розподілена за нормальним законом з математичним сподіванням  та середнім квадратичним відхиленням
та середнім квадратичним відхиленням  (стандартний нормальний розподіл). Знайти закон розподілу функції
(стандартний нормальний розподіл). Знайти закон розподілу функції  .
.
Розв’язування.
Для знаходження числових характеристик функції  можна спочатку знайти щільність розподілу
можна спочатку знайти щільність розподілу 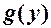 за формулою (*) або (**), а потім скористуватись означеннями. Але інколи можна знайти числові характеристики безпосередньо. Наприклад, математичне сподівання функції
за формулою (*) або (**), а потім скористуватись означеннями. Але інколи можна знайти числові характеристики безпосередньо. Наприклад, математичне сподівання функції  можна знайти за формулою
можна знайти за формулою
 ,
,
де  - щільність розподілу імовірностей ВВ
- щільність розподілу імовірностей ВВ  .
.
Приклад 7.4. НВВ  задана щільністю розподілу імовірностей
задана щільністю розподілу імовірностей
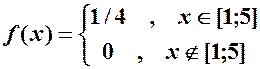
Знайти числові характеристики функції  .
.
Розв’язування.
Функції двох неперервних випадкових аргументів
Якщо кожній парі можливих значень ВВ  та
та 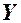 відповідає одне можливе значення ВВ
відповідає одне можливе значення ВВ  , то
, то  називають функцією двох випадкових аргументіві записують
називають функцією двох випадкових аргументіві записують 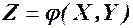 .
.
Композицією розподілів (згорткою)називається формула, за якою можна отримати закон розподілу суми незалежних ВВ.
Зазначимо, що закон розподілу суми не співпадає, взагалі кажучи, із законами розподілу доданків (навіть, якщо вони однаково розподілені).
Нехай НВВ  та
та 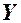 задані щільностями розподілу відповідно
задані щільностями розподілу відповідно  та
та  . Тоді щільність розподілу
. Тоді щільність розподілу 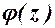 їх суми
їх суми  (за умови, що щільність розподілу хоча б одного із аргументів задана на інтервалі
(за умови, що щільність розподілу хоча б одного із аргументів задана на інтервалі 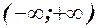 одною формулою) можна знайти за формулою, яку називають формулою композиції двох розподілів (формулою згортки):
одною формулою) можна знайти за формулою, яку називають формулою композиції двох розподілів (формулою згортки):
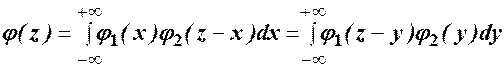 .
.
Зауваження. Якщо можливі значення аргументів невід’ємні, то щільність розподілу 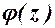 їх суми
їх суми  знаходять за формулою:
знаходять за формулою:

Приклад 7.5. Довести, що композиція двох незалежних ВВ, що розподілені за нормальними стандартними законами, також є нормально розподіленою ВВ.
Розв’язування.
Приклад 7.6. Скласти композицію двох незалежних ВВ, що розподілені рівномірно на відрізку [0;1].
Розв’язування.