Элементы векторной алгебры. Линейные векторные пространства
Элементы векторной алгебры. Линейные (векторные) пространства.
1) для любых х; у Є ЛП L сумма (х + у) Є L 2) для любых х Є L и любого числа λ произведение λ х Є L. Аксиомы:Линейная зависимость и независимость векторов линейного пространства.
Опр. Вектор α1 а1+ α2 а2+…+ αn аn Є L, где αi (i = 1,…,n)- числа, называется линейная комбинация векторов а1, а2, а3, … аn. Опр. Система векторов линейного пространства а1, а2, а3, … аn Є L называется… Опр. Система векторов а1, а2, а3, … аn Є L называется линейно зависимой (ЛЗ), если существует набор чисел α1,…Теорема о линейной зависимости системы векторов линейного пространства.
Для того чтобы система векторов линейного пространства была линейно зависимой необходимо и достаточно, чтобы какой- нибудь вектор этой системы был… Док-во: Н ( ) есть ЛЗ система. Нужно доказать, что один вектор ЛК всех… а1, а2, а3, … аn – ЛЗ система векторов, т.е. существует число ≠ 0 α1, α2 ,α3 … αn, что ЛК…Лекция 2. Размерность и базис линейного пространства.
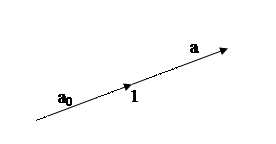
Другими словами, размерность ЛП - это максимальное количество ЛНЗ векторов, помещающихся в этом пространстве. Опр. Любые n ЛНЗ векторов ЛП размерности n l1, l2, ... ,ln называется базисом… Пр. 1) Любой не нулевой вектор на прямой ЛНЗ и является базисом ЛП всех векторов на прямой.Теорема о разложении вектора по базису.
Док-во: Рассмотрим ЛП размерностью n с базисом l1, l2, ... ,ln, вектор а Є ЛП. Система векторов l1, l2, ... ,ln, а, отсюда следует, что система ЛЗ,… Покажем, что коэффициент αn+1 ≠ 0 от противного. Допустим, что… Получили противоречие тому, что базис l1, l2, ... ,ln- ЛНЗ, отсюда следует αn+1 ≠ 0.Координаты вектора в данном базисе. Операции с векторами в координатной форме.
Рассмотрим в ЛП размерности n базис l1, l2, ... ,ln. Любой вектор ЛП разлагается в линейную комбинацию базисов. х = α1 l1+ α2 l2+ ... +αn ln (по теореме о разложении по базису), х Є ЛП.
Опр. Упорядоченный набор чисел, участвующий в разложении вектора по базису (α1, α2,… αn) называется координатами этого вектора в данном базисе.
х =( α1, α2,… αn) – координаты вектора ЛП.
Операции:
1) для того, чтобы сложить два вектора ЛП в координатной форме нужно сложить их соответствующие координаты.
Док-во: Возьмем два вектора ЛП.
|
у = (β1, β2, … βn)= β1 l1+ β2l2+…+βn ln
х + у = (α1 β1, α2 β2,… αn βn) = (α1 + β1)l1+(α2 + β2)l1+…+(αn βn)l1
2) чтобы вектор в координатной форме умножить на число нужно каждую координату умножить на это число.
Док-во: х =(α1, α2,… αn)= α1 l1+ α2 l2+ ... +αn ln
λх = (λ1α1, λ2α2,… λnαn)= λ1α1 l1+ λ2α2 l2+ ... +λnαn ln
Лекция 3. Декартовая система координат.
Координаты точки, радиус- вектор точки, произвольные вектора. Длина вектора.
Проекция вектора на ось.
Через т. А и т. В проведем плоскости ┴оси l, и найдем точки пересечения плоскости с осью. Перенесем вектор АВ в точку А1, А1В1(проекция)=АВ. Из прямоугольного… │АВ│· cos φ= AB. Проекцияl АВ= │АВ│· cos φ, где φ- это угол между вектором и…Две теоремы о проекциях.
Теорема 1 прl(а + b)= прl a + прl b
Теорема 2 прl (λа)= λ прl а
Связь между координатами вектора и проекциями вектора на координатной оси.
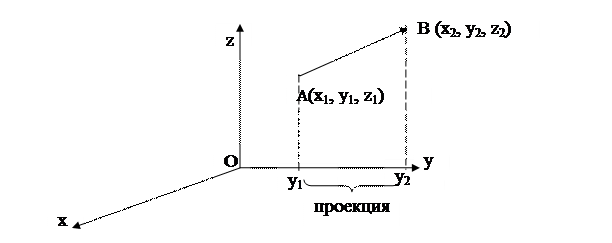
прOY АВ= y1- y2
Аналогично, что прOX АВ= x1- x2
прOZ АВ= z1- z2
Вывод: проекцией вектора на координатные оси совпадает с координатами вектора.
Условие коллинеарности двух векторов.
b= λa. В координатной форме:Лекция 4. Скалярное произведение векторов.
По определению a · b= │a││b│· cos φ - связь между скалярным произведением и проекцией вектора на вектор.Свойства скалярного произведения.
a · b= │a││b│· cos φ= │b││a│· cos φ= b · a 2° a · b= 0, т.к. a ┴ b или a или b= 0Скалярное произведение координатных ортов.
i × j= 0, так как i ^ j (из 2°)
i × k= 0, так как i ^ k (из 2°)
k × j= 0, так как k ^ j (из 2°)
i × i=│i│2 = 12=1
j × j=│j│2 = 12=1
k × k=│k│2 = 12=1
Скалярное произведение в координатной форме.
Возьмем два вектора в координатной форме
b= (bx, by, bz)= bxi + byi + bzk a × b= (axi + ayi + azk) (bxi + byi + bzk)= axi bxi + axi byi + axi bzk… ay bx i× j + ay by j× j + ay bz i× k + az bx i× k + az by k× j + az bz k× k= ax bx…Приложения скалярного произведения.
1) Угол между векторами
Ðj- острый, cos j> 0, отсюда следует, что a × b> 0
Ðj- тупой, cos j< 0, отсюда следует, что a × b< 0
Ðj= 90°, cos j= 0, отсюда следует, что a × b= 0
2) Проекция вектора на вектор
Пр. Дан треугольник АBС, т. A(2, -1, 3), т. B(4, 0, 1), т. С(-1, 3, 0). Найти угол А, прAC AB-?
Понятие евклидова пространства.
1° x × y= y × x 2° (lx) y= l(xy) 3° x (y + z)= xy + xzЛекция 5. Векторное произведение двух векторов.
1° │с│=│a││b│sin φ, где Ðj= a,b 2° вектор c ^ a, c ^b, т.е. с ^ плоскости, в которой лежат вектора а и b. 3° тройка векторов a, b, c – праваяВекторные произведения координатных ортов.
Если первый орт умножить векторно на второй орт, то по стрелке получим третий орт, причем взятый с «+», если поворот против часовой стрелке и… i´j= k i´k= -jВекторное произведение в координатной форме.
ay bx i× j + ay by j×j + ay bz i× k + az bx i× k + az by k× j + az bz k× k= ax by k - ax bx j- ay bx k+ ay bz i+… - для вычисления векторного пространства в координатной форме.Приложения векторного произведения.
1) S параллелограмма, построенного на векторах a и b, как на сторонах, численно равна модулю векторного произведения a ´ b.
Sпар=│a ´ b│
Из геометрии Sпар=│a ´ b│ sin φ из выражения │a ´ b│= │a││b│sin φ, отсюда следует, что Sпар=│a ´ b│
Следствие: из геометрии Sпар=│a│ha, 
2) 
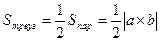
3) a ║b, отсюда следует, что a´b= 0 (из условия коллинеарности двух векторов.
│ a´b│= │a││b│sin φ= 0,
│ a´b│= 0.
Пр. Дано a= 2p – q, b= p+ 3q, │q│=2,│p│=1, Ðj = (p, q)= 
. Найти Sквад-?
Дано ∆ABC, т. А(2, -1, 3), т. B(4, 0, -2), т. С(1, -1, 3). Найти S∆-?, hAB-?
Смешанное произведение трех векторов.
По определению abc. Чтобы вычислить смешанное произведение нужно: 1) вектор a´b= векторЛекция 6. Смешанное произведение в координатной форме.
а= (ах, ау, аz)= axi + ayi + azk b= (bx, by, bz)= bxi + byi + bzk с= (сx, сy, сz)= сxi + сyi + сzkПриложение смешанного произведения.
1) Модуль смешанного произведения численно равен объему параллелепипеда, построенного на трех векторах как на ребрах.
Vпарал= │abc│
Из геометрии Vпарал= Sосн· h
Sосн= Sквад= │ a´b │ из приложения векторного произведения.
h= │с││cos φ│
Vпарал= │ a´b ││c││cos φ│=│(a´b) · с │=│abc│
Следствие: высота параллелепипеда h=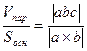 
2) Из геометрии Vтетр= Vпарал=│abc│
Vтетр= 
Sосн· h
hтетр=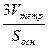 
3) Если смешанное произведение abc>0, то тройка векторов правая, если abc<0, то тройка векторов левая.
abc= (a´b) · с = │ a´b ││c││cos φ│
abc>0, cos φ >0, Ðj- острый, abc- правая тройка
abc<0, cos φ <0, Ðj- тупой, abc- левая тройка
4) abc- коллинеарные (║ одной плоскости или лежат в одной плоскости), abc=0- условие коллинеарности трех векторов.
a´b ^ плоскости α
a´b ^ с, (a´b) · с = 0 (условие перпендикулярности двух векторов), abc=0
Пр. Лежат ли четыре точки A(2, -1, 3), B(4, 0, 1), C(5, -1, 2), D() в одной плоскости?
Задание вектора в пространстве.
Любой вектор в пространстве имеет длину и направление. Длина вектора │а│=
. Направление вектора задают три направляющих cos → cos α, cos β, cos γ, где Ðα- угол между а и ОХ, Ðβ- угол между а и ОУ, Ðγ- угол между а и OZ.
Ðα= a, i
Ðβ= a, j
Ðγ = a, k
cos α=
cos β=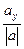
cos γ=
Свойство направляющих косинусов:
cos2 α+ cos2 β+ cos2 γ= 1
Опр. Единичный вектор, имеющий своими координатами направляющие cos вектора а называется единичным вектором направления а и обозначается а0= (cosα, cosβ, cosγ).
Аналитическая алгебра.
Лекция 1. Плоскость в пространстве.
N= (A, B, C) Пусть т. М0 (x0, y0, z0)- произвольная фиксированная точка плоскости, т. М (x,…Анализ общего уравнения.
нет х, нормаль N= (0, B, C) скалярное произведение N· i= 0· 1+ B· 0+ C· 0= 0, N ^ i, N ^ OX, плоскость… Аналогично, В=0, нет у, плоскость ║ОУ,Уравнение плоскости, проходящей через 3 точки.
Пусть т. М1(x1, y1, z1) т. М2 (x2, y2, z2) Є плоскости т. М3(x3, y3, z3)Уравнение плоскости в отрезках.
т. А (а, 0, 0) т. В (0, b, 0) Є плоскости т. C (0, 0, c)Взаимное расположение двух плоскостей.
Плоскость 1 ║ плоскости 2, отсюда следует, что ║. Координаты коллинеарных векторов пропорциональны. - условие параллельности двух плоскостей. Если , то такие плоскости будут… 2) Плоскость 1 ^ плоскости 2Прямая в пространстве.
l= (m; n; p) ║прямой S- в подобиях т. М0- произвольная фиксированная точка прямойЛекция 2. Общие уравнения прямой в пространстве.
- общее уравнение прямой в пространстве. Замечание: такое задание прямой не однозначно.Переход от одних уравнений прямой к другим.
Взаимное расположение прямых в пространстве.
l1 ║ l2,отсюда следует, что - условие параллельности двух прямых в…Взаимное расположение прямой и плоскости в пространстве.
Возможны следующие случаи расположения: 1) Прямая ^ плоскости. N║l, - условие перпендикулярности прямой и плоскости.Различные расстояния в пространстве.
Найдем расстояние от т. М0 (x0, y0, z0) до плоскости Ax+ By+ Cz+ D=0. Рассмотрим от точки до плоскости это длина перпендикуляра, опущенного из точки… а) Составим параметрические уравнения прямойРасстояние между двумя параллельными плоскостями.
На одной плоскости нужно взять произвольную точку и найти расстояние от этой точки до другой плоскости.
Расстояние между прямой и параллельной плоскостью.
Расстояние от точки до прямой.
Проведем через т. М0 плоскость перпендикулярную прямой (проектирующая плоскость). Найдем точку пересечения прямой и плоскости. а) Составим уравнение плоскостиЛекция 3. Прямая на плоскости.
М (х, у)Взаимное расположение прямых на плоскости.
Пр. Дан прямоугольник АВС, т. А(2, 1), т. В(3, 0), т. С(-4, 2). Найти…Лекция 4. Кривые второго порядка.
Общее уравнение 
. Будем рассматривать окружность, эллипс, гиперболу, параболу.