Действия над векторами, заданными своими координатами

Определение 3.4 Проекцией вектора 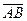на ось называется число, равное длине вектора (рис. 3.9), взятое со знаком «плюс», если направление вектора совпадает с направлением оси и со знаком «минус» в противном случае.

Точки 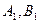- это точки пересечения оси с плоскостями, проходящими через точк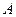и и 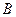, перпендикулярно оси . Обозначение .

Основные свойства проекции:

1) , где 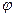- угол между вектором 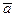и осью ;

2) ;

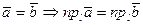3) ;

4) .

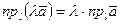Рассмотрим в пространстве прямоугольную систему координат 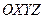. Построим на координатных осях 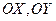и единичные векторы, обозначаемые соответственно (рис. 3.10).

Единичные векторы , имеющие направление положительных координатных полуосей, называются ортами координатныхосей.

Произвольный вектор 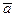пространства можно единственным образом представить в виде линейной комбинации ортов координатных осей. Для разложения вектора 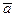совместим его начало с началом координат (рис. 3.10). Из конца 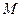вектора 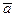проведем плоскости, параллельные координатным плоскостям. Обозначи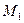м , и точки пересечения этих плоскостей с осями соответственно. Тогда

,

, , .

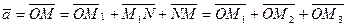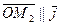а значит, существуют числа 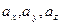, такие что

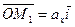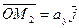, , и

, , .

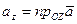Следовательно, вектор 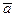можно представить в виде:

. (3.5)

Формула (3.5) называется разложением вектора 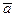по ортам координатных осей или по базису . Коэффициенты линейной комбинации (3.5) называют прямоугольными координатами вектора 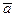, т.е. координаты вектора есть его проекции на соответствующие координатные оси.

Векторное равенство (3.5) записывают в виде

(3.6)

Имеет место аналогичное разложение вектора 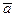по базису 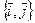на плоскости (рис. 3.11).

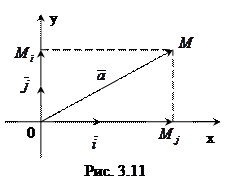
. (3.7)

Длина вектора 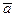с координатами определяется по формуле

. (3.8)

Для плоского вектора

. (3.9)

Направление вектора 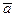в пространстве и на плоскости можно определить с помощью косинусов углов, которые образует вектор с осями координат. Их называют направляющими косинусами вектора. Обозначим 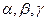- углы, которые составляет вектор 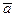с осями соответственно, тогда

, , . (3.10)

Справедливо равенство

. (3.11)

При выполнении линейных операций над векторами тем же операциям подвергнутся и их проекции на координатные оси.

Пусть даны два вектора 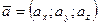и .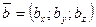

При сложении векторов их одноименные координаты складываются, при вычитании – вычитаются, при умножении на число – умножаются на это число:

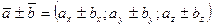, (3.12)

.

Векторы 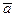и 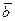равны тогда и только тогда, когда равны их соответствующие координаты:

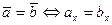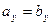, , . (3.13)

Векторы 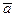и 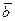коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е.

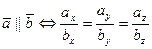. (3.14)

 

Радиус-вектором точки 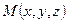называется вектор (рис. 3.12), начало которого совпадает с началом координат, а конец с точкой .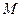

Координаты точки – это координаты её радиус-вектора .

Для вектора 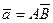, заданного координатами точк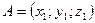и и 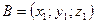, его координаты определяются из векторного равенства

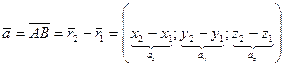(3.15)

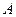Здесь и - радиус-векторы точек и 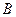, т.е. координаты вектора 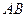равны разностям одноименных координат конечной 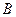и начальной 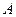точек этого вектора.