Линейная зависимость и независимость векторов. Базис.
Определение 9. Векторы  называются линейно не-зависимыми, если равенство
называются линейно не-зависимыми, если равенство
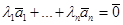 (2) выполняется только при условии
(2) выполняется только при условии 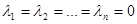 . Если в равенстве (2) хотя бы один из коэффициентов отличен от нуля, то векторы
. Если в равенстве (2) хотя бы один из коэффициентов отличен от нуля, то векторы 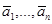 называются линейно зависимыми.
называются линейно зависимыми.
Утверждение 1.Система ненулевых векторов зависима тогда и только тогда, когда некоторый вектор линейно выражается че-рез остальные.
Доказательство.а) Пусть векторы 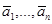 линейно зависимы , тогда в равенстве (2) хотя бы один из коэффициентов отличен от нуля, например,
линейно зависимы , тогда в равенстве (2) хотя бы один из коэффициентов отличен от нуля, например, 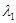
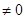 .В этом случае получаем
.В этом случае получаем
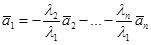 , то есть вектор
, то есть вектор  линейно выражается через остальные.
линейно выражается через остальные.
б) Пусть какой-то из векторов линейно выражается через ос-тальные, например, вектор  , то есть
, то есть 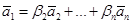 , тогда
, тогда  , коэффициент при
, коэффициент при  отличен от нуля, следовательно, по определению, векторы линейно зависи-мы.
отличен от нуля, следовательно, по определению, векторы линейно зависи-мы.
Утверждение 2.Для того, чтобы два вектора были линейно за-висимыми, необходимо и достаточно, чтобы они были колли-неарными.
Доказательство.а) Пусть векторы 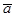 и
и 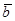 линейно зависимы, тогда один из векторов линейно выражается через другой, на-пример,
линейно зависимы, тогда один из векторов линейно выражается через другой, на-пример,  , а это и означает, что векторы коллинеарны.
, а это и означает, что векторы коллинеарны.
б) Пусть векторы 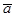 и
и 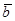 коллинеарны, то есть
коллинеарны, то есть  , значит,
, значит, 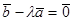 , коэффициент при
, коэффициент при 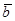 отличен от нуля, следователь-но, по определению, векторы линейно зависимы.
отличен от нуля, следователь-но, по определению, векторы линейно зависимы.
Утверждение 3.Для того, чтобы три вектора были линейно зависимыми, необходимо и достаточно, чтобы они были ком-планарными.
Доказательство.а)Пусть векторы 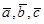 линейно зависимы, тогда один из них линейно выражается через остальные, на-пример,
линейно зависимы, тогда один из них линейно выражается через остальные, на-пример, 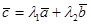 , отнесем эти векторы к одному началу, проведем через векторы
, отнесем эти векторы к одному началу, проведем через векторы 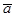 и
и 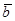 плоскость
плоскость 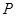 , тогда векторы
, тогда векторы 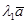 и
и  будут тоже принадлежать этой плоскости, следо-вательно, вектор
будут тоже принадлежать этой плоскости, следо-вательно, вектор 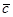 принадлежит плоскости
принадлежит плоскости 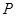 , то есть векторы компланарны.
, то есть векторы компланарны.
б) Пусть векторы 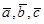 компланарны, перенесем их в одну точку плоскости, если векторы
компланарны, перенесем их в одну точку плоскости, если векторы 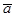 и
и 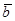 не коллинеарны, то
не коллинеарны, то 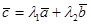 , то есть
, то есть 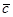 линейно выражается через
линейно выражается через 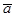 и
и 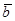 , это означает, что векторы линейно зависимы; если векторы
, это означает, что векторы линейно зависимы; если векторы 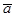 и
и 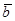 коллинеарны, то есть
коллинеарны, то есть  , то
, то 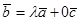 , значит вектор
, значит вектор 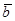 линейно выражается через векторы
линейно выражается через векторы 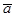 и
и 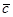 , следовательно, векторы линейно зависимы.
, следовательно, векторы линейно зависимы.

Рис.10
Определение 10.Совокупность линейно независимых векторов таких, что любой вектор линейно выражается через эти векторы, называется базисом.
Из утверждения 2 следует, что на плоскости базисом могут быть любые два неколлинеарных вектора. Из утверждения 3 следует, что в пространстве базисом могут служить любые три некомп-ланарных вектора. Если векторы 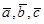 образуют базис, то произвольный вектор
образуют базис, то произвольный вектор 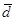 линейно выражается через эти векторы, то есть
линейно выражается через эти векторы, то есть 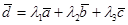 , тогда числа
, тогда числа  являются координатами вектора
являются координатами вектора 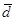 в данном базисе (
в данном базисе (  ).
).