Аффинная система координат в пространстве.
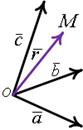
Рис.17
Пусть дана тройка ненулевых некомпланарных векторов 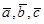 , отнесенных к общему началу в точку
, отнесенных к общему началу в точку  . Эти векторы линейно независимы, поэтому их можно принять за базис. Про-извольный вектор
. Эти векторы линейно независимы, поэтому их можно принять за базис. Про-извольный вектор 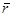 линейно выражается через данные векторы, то есть
линейно выражается через данные векторы, то есть 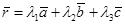 . Векторы
. Векторы 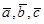 образуют аффин-ную систему координат в пространстве, точка
образуют аффин-ную систему координат в пространстве, точка  - начало этой системы координат, числа
- начало этой системы координат, числа  - это аффинные координаты вектора. Возьмем произвольную точку
- это аффинные координаты вектора. Возьмем произвольную точку  , вектор, соединяю-щий данную точку с началом координат, называется радиус-век-тором точки и обозначается
, вектор, соединяю-щий данную точку с началом координат, называется радиус-век-тором точки и обозначается 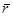 , координаты радиус-вектора яв-ляются координатами этой точки.
, координаты радиус-вектора яв-ляются координатами этой точки.
Аналогично определяется аффинная система координат на плос-
кости.
2. Декартова система координат в пространстве.
Рассмотрим три взаимно перпендикулярные оси, пересекающие-
ся в одной точке  . Они образуют прямоугольную или декарто-
. Они образуют прямоугольную или декарто-
ву систему координат в пространстве.

Рис.18
Ось 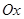 называется осью абсцисс, ось
называется осью абсцисс, ось 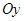 - осью ординат,
- осью ординат,  - осью аппликат. Каждой оси соответствует базисный орт:
- осью аппликат. Каждой оси соответствует базисный орт:  . Произвольный вектор
. Произвольный вектор 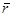 линейно выражается через базисные орты:
линейно выражается через базисные орты: 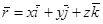 .Координаты вектора
.Координаты вектора 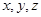 - проекции вектора
- проекции вектора 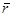 на оси координат.
на оси координат.
Если заданы координаты векторов 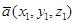 и
и  ,
,
то операции над векторами выполняются следующим образом:
а) 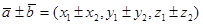 ;
;
б)  .
.
Если векторы 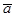 и
и 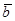 коллинеарны, то их координаты пропор-циональны, то есть
коллинеарны, то их координаты пропор-циональны, то есть
 (5)
(5)
Определение 15.Направляющими косинусами вектора назы-ваются косинусы углов, которые вектор образует с осями коор-динат.
Так как 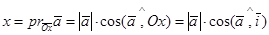 , то
, то
 (6)
(6)
Пусть заданы координаты начальной точки вектора  и конечной точки
и конечной точки  . Надо найти координаты вектора
. Надо найти координаты вектора 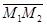 .
.
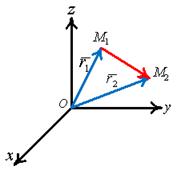
Рис.19
 , следовательно,
, следовательно,
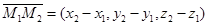 (7)
(7)
Длину вектора можно найти по формулам:
 (8)
(8)
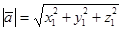 (9)
(9)
Рассмотрим задачу деления отрезка в заданном отношении.

Рис.20
Пусть точка  делит отрезок так, что
делит отрезок так, что 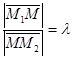 или
или 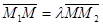 , тогда
, тогда 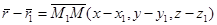 ,
,  , отсюда следует, что
, отсюда следует, что
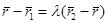 , если из этого равенства выразить
, если из этого равенства выразить 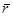 , получим формулу:
, получим формулу:
 (10)
(10)
или в координатной форме:

 (11)
(11)
Если точка  делит отрезок пополам, то есть
делит отрезок пополам, то есть 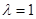 , то форму-лы (11) примут вид:
, то форму-лы (11) примут вид:
 (12)
(12)
Аналогично определяется декартова система координат на плос-кости и имеют место аналогичные формулы.
3.Полярная система координат на плоскости.
Задается точка  , которая называется полюсом, луч
, которая называется полюсом, луч 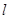 , исхо-дящий из данной точки, называемый полярной осью. Это поляр-ная система координат.
, исхо-дящий из данной точки, называемый полярной осью. Это поляр-ная система координат.
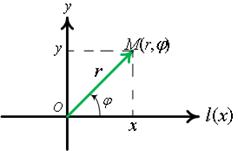
Рис.21
Положение точки  относительно этой системы координат определяется двумя числами
относительно этой системы координат определяется двумя числами  и
и  .
.  =
= - это длина век-тора, соединяющего точку с полюсом;
- это длина век-тора, соединяющего точку с полюсом;  - угол между полярной осью и вектором
- угол между полярной осью и вектором  . У полюса
. У полюса  - не опрелен. Для ос-тальных точек
- не опрелен. Для ос-тальных точек 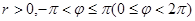 .
.
Можно найти связь между полярными и декартовыми коор-динатами. Для этого начало декартовой системы совмещают с полюсом, ось 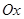 с полярной осью. Получим следующие формулы:
с полярной осью. Получим следующие формулы:
 (13)
(13)
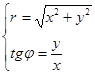 (14)
(14)