Тема 5. Комбінації плоских фігур
81. Коло дотикається до більшого катета прямокутного трикутника, проходить через вершину протилежного гострого кута і має центр на гіпотенузі трикутника. Знайти радіус кола, якщо катети трикутника рівні 5 і 12.
82. Коло дотикається до одного з катетів рівнобедреного прямокутного трикутника і проходить через вершину протилежного гострого кута. Знайти радіус кола, якщо його центр лежить на гіпотенузі трикутника, а катет трикутника рівний а.
83. Бічна сторона рівнобедреного трикутника рівна 10 см, основа – 12 см. До кола, вписаного в трикутник, проведені дотичні, які паралельні висоті трикутника і відтинають від даного трикутника два прямокутні трикутники. Знайти сторони цих трикутників.
84. Хорда кола, рівна 16 см, знаходиться на відстані 15 см від його центра. Знайти площу трикутника, описаного навколо кола, якщо периметр трикутника рівний 200 см.
85. На стороні рівнобедреного прямокутного трикутника з гіпотенузою с поза цим трикутником побудовані квадрати. Центри цих квадратів з’єднані між собою. Знайти площу утвореного трикутника.
86. Знайти відношення площ квадрата, правильного трикутника та правильного шестикутника, які вписані в одне й те саме коло.
87. На діаметрі 2R півкола побудований правильний трикутник, сторона якого рівна діаметру. Трикутник розміщений по ту сторону від діаметра, що й півколо. Знайти площу тієї частини трикутника, яка лежить поза колом.
88. Гіпотенуза прямокутного трикутника рівна с, а один з гострих кутів дорівнює  . Знайти радіус кола з центром у вершині цього кута, яке ділить трикутник на дві рівновеликі частини.
. Знайти радіус кола з центром у вершині цього кута, яке ділить трикутник на дві рівновеликі частини.
89. У рівнобедреному трикутнику АВС (АВ = ВС) на основі АС взято точку М так, що АМ = а, МС = b. У трикутники АВМ і СВМ вписані кола. Знайти відстань між точками дотику цих кіл зі стороною ВМ.
90. У паралелограмі зі сторонами а і b і кутом проведені бісектриси чотирьох кутів. Знайти площу чотирикутника, обмеженого бісектрисами.
91. У ромб з висотою h і гострим кутом 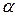 вписано коло. Знайти радіус більшого з двох можливих кіл, кожне з яких дотикається до даного кола і двох сторін ромба.
вписано коло. Знайти радіус більшого з двох можливих кіл, кожне з яких дотикається до даного кола і двох сторін ромба.
92. На колі радіуса r вибрані три точки таким чином, що коло виявилося розділеним на три дуги, довжини яких відносяться як 3:4:5. У точках поділу до кола проведені дотичні. Знайти площу трикутника, утвореного цими дотичними.
93. Дано відрізок довжини а. Три кола радіуса R 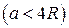 мають центри в кінцях відрізка і в його середині. Знайти радіус четвертого кола, яке дотикається до трьох даних.
мають центри в кінцях відрізка і в його середині. Знайти радіус четвертого кола, яке дотикається до трьох даних.
94. Дано квадрат зі стороною а. Знайти площу правильного трикутника, одна вершина якого збігається з серединою однієї із сторін квадрата, а дві інші розміщені на діагоналях квадрата.
95. Через вершини А і В трикутника АВС проведено коло радіуса r, яке перетинає сторону ВС у точці D. Знайти радіус кола, що проходить через точки A, D і C, якщо AB = c, AC = b.
96. Сторона AB квадрата ABCD рівна 1 і є хордою деякого кола, до того ж інші сторони квадрата лежать поза цим колом. Довжина дотичної CK, проведеної з вершини C до цього ж кола, рівна 2. Знайти діаметр кола.
97. У паралелограмі ABCD відомі AB = a, BC = b, 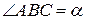 . Знайти відстань між центрами кіл, які описані навколо трикутників BCD і DAB.
. Знайти відстань між центрами кіл, які описані навколо трикутників BCD і DAB.
98. Знайти площу спільної частини двох рівних квадратів зі стороною а і один утворюється з іншого поворотом навколо вершини на кут 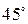 .
.
99. Коло радіуса R проходить через вершини A і B трикутника ABC і дотикається до прямої AC у точці A. Знайти площу трикутника ABC, знаючи, що 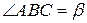 і
і 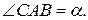
100. В прямокутному трикутнику АВС з катетами АВ = 3 і ВС = 4 через середини сторін АВ і АС проведено коло, яке дотикається до сторони ВС. Знайти довжину відрізка гіпотенузи АС, який лежить всередині цього кола.
 |
 |