Алгебра множеств. Осн. тождества алгеб. множеств

Множества вместе с определенными на них операциями образуют алгебру множеств. Последовательность выполнения операций задается с помощью формулы алгебры множеств. Например, 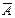Ç (ВÈC), (А В) + C – формулы алгебры множеств.

Двойное дополнение. = A.

Закон исключенного третьего. A È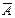= U.

№6. Операции с пустым и универсальным множествами.

а) A È U = U; б) A È Æ = A; в) A Ç U = A;г) A Ç Æ = Æ; д) = U; е) = Æ.

№7. Эквивалентность множеств

Определение.Если каждому элементу множества A сопоставлен единственный элемент множества B и при этом всякий элемент множества B оказывается сопоставленным одному и только одному элементу множества A, то говорят, что между множествами A и B существует взаимно однозначное соответствие. Множества A и B в этом случае называют эквивалентными или равномощными.

Эквивалентность множеств обозначается следующим образом: A ~ B.

Эквивалентность множеств обладает следующим свойством транзитивности.

Если A ~ B и B ~ C, то A ~ C.

№8. Мощностью конечного множества А (обозначается çАç) называется число элементов этого множества. Например, мощность множества А = {1, 2} равна çАç= 2.

çАÈB ç= çА ç+ çB ç– çАÇB/; çАÈBÈ Сç= çА ç+ çB ç+ çC ç– çАÇB ç– çАÇC ç– çBÇC ç+ çАÇB ÇC ç

Если множества А_i попарно не пересекаются, т.е. А_i ÇА_j = Æ, i ¹ j, то получим частный случай формулы:

çА₁È А₂ È…ÈА_nç= çА₁ç+çА₂ç+…+ çА_nç.

№9. Счетные множества

Определение Множество, эквивалентное множеству натуральных чисел N = {1, 2, 3, …, n,…}, называется счетным. Можно сказать также, что множество счетно, если его элементы можно перенумеровать.

Следующие множества являются счетными: 1. A₁ = {–1, –2, …, – n, …}; 2. A₂ = {2, 2², …, 2ⁿ,…};

Чтобы установить счетность некоторого множества, достаточно указать взаимно однозначное соответствие между элементами данного множества и множества натуральных чисел.

Теорема 1. Всякое бесконечное подмножество счетного множества счетно.

Теорема 2. Объединение конечной или счетной совокупности счетных множеств счетно.

Теорема 3. Множество всех рациональных чисел, т.е. чисел вида 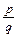, где p и q целые числа, счетно.

Теорема 4. Если А = {a₁, a₂, …} и B = {b₁, b₂, …} – счетные множества, то множество всех пар С = {(a_k, b_n), k = 1, 2,…; n = 1, 2, …} счетно.

Теорема 5. Множество всех многочленов P(x) = a₀ + a₁x + a₂x² + … + a_nxⁿ любых степеней с рациональными коэффициентами a₀, a₁, a₂, … a_n счетно.

Теорема 6.Множество всех корней многочленов любых степеней с рациональными коэффициентами счетно.

№10. Множества мощности континуума

Существуют бесконечные множества, элементы которых нельзя перенумеровать. Такие множества называются несчетными.

Теорема Кантора. Множество всех точек отрезка [0, 1] несчетно.

Множество, эквивалентное множеству всех точек отрезка [0, 1] называется множеством мощности континуума. Так как множества точек интервалов, отрезков и всей прямой эквивалентны между собой, то все они имеют мощность континуума. Чтобы доказать, что данное множество имеет мощность континуума, достаточно указать взаимно однозначное соответствие между данным множеством и множеством точек отрезка, интервала или всей прямой.

Теорема 1. Множество всех подмножеств счетного множества счетно.

Теорема 2. Множество иррациональных чисел имеет мощность континуума.

Теорема 3. Множество всех точек n-мерного пространства при любом n имеет мощность континуума.

Теореа 4. Множество всех комплексных чисел имеет мощность континуума.

Теорема 5.Множество всех непрерывных функций, определенных на отрезке [a, b] имеет мощность континуума.