Упорядоченная пара, прямое декартово произведение

Если задана пара {a, b} , то множество {a, {a, b}} называется упорядоченной парой и обозначается(a, b) . При этом элемент a называется первым элементом, а элемент b — вторым элементом пары. В формальной математике первый элемент упорядоченной пары A=(a, b)называется также первой координатой или первой проекцией и обозначается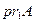. Аналогично второй элемент парыA называется второй координатой или второй проекцией и обозначается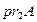. Прямое или декартово произведение — множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих разделах математики благодаря тому, что прямое произведение часто наследует структуры (алгебраические, топологические и т. д.), существующие на перемножаемых множествах..

12. Бинарное отношение, матрица бинарного отношения. Бинарным отношением между элементами множеств А и В называется любое подмножество RÍA´B. Если множества A и B совпадают А=В, то R называют бинарным отношением на множестве А.

Если (x, y)ÎR, то это обозначают еще xRy и говорят, что между элементами x и y установлено бинарное отношение R.

Диагональ множества A´A, т.е. множество D={(x,x) | xÎA}, называется единичным бинарным отношением или отношением равенства в A.

Областью определения бинарного отношения R называется множество d_R={ xÎA | yÎB, (x, y) ÎR }.

Областью значений бинарного отношения R называется множество

r_R={ yÎB | xÎA, (x, y)ÎR }.

Образом множества X относительно отношения R называется множество R(X) = { yÎB | xÎX, (x, y)ÎR };

прообразом X относительно R называется R ^-1(X).

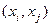
Бинарные отношения могут обладать различными свойствами такими как:\1) Рефлексивность2) Антирефлексивность (иррефлексивность): 3)Симметричтоное5) Транзитивность.6) АнтисимметричностьМатричное задание. Оно используется когда А - конечноемножество А={x_i}. Тогда отношение R можно задавать с помощью матрицы R={x_ij}, элементы которой определяются соотношением:1, если R

13. Операции над отношениямиОперации над бинарными отношениями определяются подобно операциям над соответствующими множествами. Пусть А – произвольное множество на котором введены бинарные отношения R, R₁, R₂,...

1) Объединение двух бинарных отношений R₁ и R₂ - это отношение

R₁ÈR₂ = { (x, y) | (x, y)ÎR₁ или (x, y)ÎR₂ }.

2) Пересечение двух бинарных отношений R₁ и R₂ - это отношение

R₁ÇR₂ = { (x, y) | (x, y)ÎR₁ и (x, y)ÎR₂ }.

3) Обратное отношение R ^–1 = { (x, y) | (y, x)ÎR}.

4) Дополнение к отношению 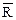={ (x, y) | (x, y)Î(A´A)R}.

5) Двойственное отношение R^d = .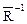

6) Композиция (суперпозиция) отношений R=R₁oR₂ содержит пару (x, y) тогда и только тогда, когда существует такое zÎA, что (x, y)ÎR₁ и (z, y)ÎR₂.

7) R₁ содержится в R₂ (R₁Í R₂), если любая пара (x, y), которая принадлежит отношению R₁ также принадлежит и отношению R₂.

Обратное отношение – это отношение, взятое в обратном порядке по отношению к данному. Пусть на множестве Х задано бинарное отношение R, тогда его обратным отношением называется отношение 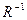, построенное следующим образом:

Cвойства: если отношение обладает одним из перечисленных свойств: рефлексивностью, нерефлексивностью, симметрией, антисимметрией, асимметрией, транзитивностью или полнотой, то и обратное отношение также обладает им..