Композиция отношений
Композицией (произведением, суперпозицией) бинарных отношений  и
и называется такое отношение
называется такое отношение , что:
, что:

Бинарное отношение R называется композицией двух отношений Р и Q тогда, когда существуют x, y, z такие, что если <х, z>∈ Р и <z, у>∈ Q, то <x, y>∈ R.По определению, P1∘P2 = Q = {(x, y) |∃z: (x,z) ∈P1 ⋀ (z,y) ∈P2}. Композиция это отношение всех таких (x, y), для которых найдется промежуточныйz, причем (x, z) ∈P1 и (z,y) ∈P2. Вот например 4. Нужно найти отношение, для которого будет существовать такой z, а потом показать равенство отношений (вложенность туда-обратно). R1(x, z) = {(x, z) | x3 = z2} = [так как z2 ≥ 0, то x3 ≥ 0, поэтому можно извлекать корень] = {(x, z) | x3/2 = z, x ≥ 0} R2(z, y) = {(z, y) | z + y = 7 }. Объединяя, получаем R1∘R2 = {(x, y) | x3/2 + y = 7, x ≥ 0}. Условие композиции будет выполняться: ∃z = x3/2: (x, z) ∈R1 ⋀ (z,y) ∈R2 (для полного решения нужно доказать равенство этих отношений)
15. Рефлексивность . Бинарное отношение R на множестве Х называется рефлексивным, если всякий элемент этого множества находится в отношение R с самим собой. Формально отношение R рефлексивно, если
. Бинарное отношение R на множестве Х называется рефлексивным, если всякий элемент этого множества находится в отношение R с самим собой. Формально отношение R рефлексивно, если 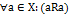
 Cвойстворефлексивности при заданных отношениях матрицей характеризуетс тем, что все диагональные элементы матрицы равняются 1;при заданных отношениях графом каждый элемент имеет петлю – дугу (х, х).Вот задано какое-то отображение Т на множестве, так что у = Т(х) Говорят, что оно рефлексивно, если для любого х из множества утверждение х = Т(х) справедливо.
Cвойстворефлексивности при заданных отношениях матрицей характеризуетс тем, что все диагональные элементы матрицы равняются 1;при заданных отношениях графом каждый элемент имеет петлю – дугу (х, х).Вот задано какое-то отображение Т на множестве, так что у = Т(х) Говорят, что оно рефлексивно, если для любого х из множества утверждение х = Т(х) справедливо.
Пример. Отношение равенства в поле действительных чисел. Оно рефлексивно, так как любое число равно самому себе.
Рефлексивность, свойство бинарных (двуместных, двучленных) отношений, выражающее выполнимость их для пар объектов с совпадающими членами (так сказать, между объектом и его «зеркальным отражением»): отношение R называется рефлексивным, если для любого объекта х из области его определения выполняется xRx. Типичные и наиболее важные примеры рефлексивных отношений: отношения типа равенства (тождества, эквивалентности, подобия и т.п.: любой предмет равен самому себе) и отношения нестрогого порядка (любой предмет не меньше и не больше самого себя). Интуитивные представления о «равенстве» (эквивалентности, подобии и т.п.), очевидным образом наделяющие его свойствами симметричности и транзитивности, «вынуждают» и свойство Рефлексивность, поскольку последнее свойство следует из первых двух. Поэтому многие употребительные в математике отношения, по определению Рефлексивность не обладающие, оказывается естественным доопределить таким образом, чтобы они становились рефлексивными, например, считать, что каждая прямая или плоскость параллельна самой себе, и т.п.