Тема 2.2 Пределы и непрерывность

Ключевые понятия: предел функции, предел последовательности, свойства пределов; бесконечно малые и бесконечно большие величины.

Предел последовательности

Число a называется пределом последовательности x = {x_n}, если для произвольного заранее заданного сколь угодно малого положительного числа ε найдется такое натуральное число N, что при всех n>N выполняется неравенство |x_n - a| < ε.

Если число a есть предел последовательности x = {x_n}, то говорят, что x_n стремится к a, и пишут .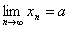

Чтобы сформулировать это определение в геометрических терминах введем следующее понятие.

Окрестностью точки x₀ называется произвольный интервал (a, b), содержащий эту точку внутри себя. Часто рассматривается окрестность точки x₀, для которой x₀ является серединой, тогда x₀ называется центром окрестности, а величина (b–a)/2 – радиусом окрестности.

Итак, выясним, что же означает геометрически понятие предела числовой последовательности. Для этого запишем последнее неравенство из определения в виде

Это неравенство означает, что все элементы последовательности с номерами n>N должны лежать в интервале (a – ε; a + ε).

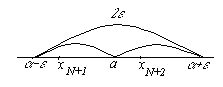Следовательно, постоянное число a есть предел числовой последовательности {x_n}, если для любой малой окрестности с центром в точке a радиуса ε (ε – окрестности точки a) найдется такой элемент последовательности с номером N, что все последующие элементы с номерами n>N будут находиться внутри этой окрестности.

Предел функции

Пусть функция y=f(x) определена в некоторой окрестности точки a. Предположим, что независимая переменная x неограниченно приближается к числу a. Это означает, что мы можем придавать х значения сколь угодно близкие к a, но не равные a. Будем обозначать это так x→a. Для таких x найдем соответствующие значения функции. Может случиться, что значения f(x) также неограниченно приближаются к некоторому числу b. Тогда говорят, что число b есть предел функции f(x) при x→a.

Введем строгое определение предела функции.

Функция y=f(x) стремится к пределу b при x→a, если для каждого положительного числа ε, как бы мало оно не было, можно указать такое положительное число δ, что при всех x ≠ a из области определения функции, удовлетворяющих неравенству |x-a|<δ, имеет место неравенство |f(x -b| < ε. Если b есть предел функции f(x) при x→a, то пишут или f(x)→b при x→a.

Проиллюстрируем это определение на графике функции. Т.к. из неравенства |x-a|<δ должно следовать неравенство |f(x)-b|<ε, т.е. при x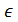(a-δ, a+δ) соответствующие значения функции f(x)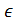(b-ε, b+ε), то, взяв произвольное ε>0, мы можем подобрать такое число δ, что для всех точек x, лежащих в δ – окрестности точки a, соответствующие точки графика функции должны лежать внутри полосы шириной 2ε, ограниченной прямыми y=b–ε и y=b+ε.

Несложно заметить, что предел функции должен обладать теми же свойствами, что и предел числовой последовательности, а именно и если при x→a функция имеет предел, то он единственный.

 

Бесконечно большие величины

Мы рассмотрели случаи, когда функция f(x) стремилась к некоторому конечному пределу b при x→a или x→∞.

Рассмотрим теперь случай, когда функция y=f(x) стремится к бесконечности при некотором способе изменения аргумента.

Функция f(x) стремится к бесконечности при x→a, т.е. является бесконечно большой величиной, если для любого числа М, как бы велико оно ни было, можно найти такое δ>0, что для всех значений х≠a, удовлетворяющих условию |x-a|<δ, имеет место неравенство |f(x)|>M.

Если f(x) стремится к бесконечности при x→a, то пишут или f(x)→∞ при x→a.

Сформулируйте аналогичное определение для случая, когда x→∞.

Если f(x) стремится к бесконечности при x→a и при этом принимает только положительные или только отрицательные значения, соответственно пишут 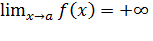или

 

Вопросы для самоконтроля:

1. Сформулируйте определение предела последовательности.

2. Сформулируйте определение предела функции в точке.

3. Укажите, какая функция называется бесконечно большой величиной.