Тема 3.1 Производная функции

Ключевые понятия: производная функции в точке; геометрический смысл производной, уравнение касательной, уравнение нормали к кривой; физический смысл производной; формулы и правила дифференцирования.

Производной функции f(x) в точке х = х₀ называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.

 

 

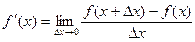
у

f(x)

 

 

f(x₀ +Dx) P

Df

f(x₀) M

 

a b Dx

0 x₀ x₀ + Dx x

 

 

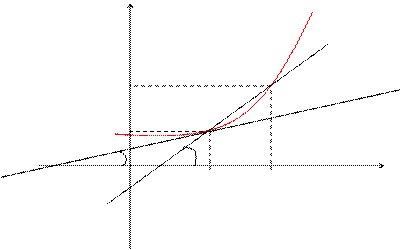
Пусть f(x) определена на некотором промежутке (a, b). Тогда тангенс угла наклона секущей МР к графику функции.

 

,

 

где a - угол наклона касательной к графику функции f(x) в точке (x₀, f(x₀)).

 

Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

 

Уравнение касательной к кривой:

 

Уравнение нормали к кривой: .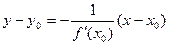

 

Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.

Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.

Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение.

Теорема. (Необходимое условие существования производной) Если функция f(x) имеет производную в точке х₀, то она непрерывна в этой точке.

Это условие не является достаточным.

 

Основные правила дифференцирования

Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.

1) (u ± v)¢ = u¢ ± v¢

2) (u×v)¢ = u×v¢ + u¢×v

3), если v ¹ 0

Эти правила могут быть легко доказаны на основе теорем о пределах.

 

Производные основных элементарных функций

С¢=0;

(x^m)¢ = mx^m-1;

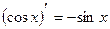
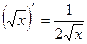
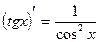
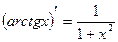
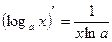
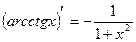
Вопросы для самоконтроля:

1. Сформулируйте определение производной. В чем заключается ее геометрический и физический смысл.

2. Запишите основные правила дифференцирования.

3. Составьте таблицу производных основных элементарных функций.