Определение случайной величины

Случайной величиной называется функция 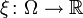, измеримая относительно иборелевской σ-алгебры на .

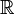Случайную величину можно определить и другим эквивалентным способом^[4]. Функция 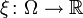называется случайной величиной, если для любых вещественных чисел 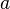и 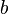множество событий 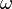, таких что 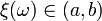, принадлежит .

 

Теорема Муавра — Лапласа — одна из предельных теорем теории вероятностей, установлена Лапласом в 1812 году. Если при каждом из n независимых испытаний вероятность появления некоторого случайного события Е равна р (0<р<1) и m — число испытаний, в которых Е фактически наступает, то вероятность неравенства близка (при больших n) к значению интеграла Лапласа.

Применение

Используется в теории вероятностей.

При рассмотрении количества 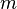появлений события 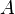в испытаниях Бернулли чаще всего нужно найти вероятность того, что 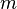заключено между некоторыми значениями 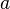и 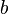. Так как при достаточно больших промежуток 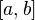содержит большое число единиц, то непосредственное использование биномиального распределения

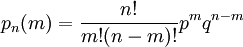
требует громоздких вычислений, так как нужно суммировать большое число определённых по этой формуле вероятностей.

Поэтому используют асимптотическое выражение для биномиального распределения при условии, что 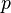фиксировано, а 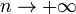. Теорема Муавра-Лапласа утверждает, что таким асимптотическим выражением для биномиального распределения является нормальная функция.

Формулировка

Если в схеме Бернулли n стремится к бесконечности, p (0 < p < 1) постоянно, величина 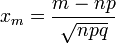ограничена равномерно по m и n 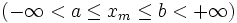, то

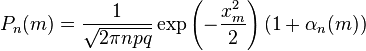
где 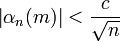, c > 0, c — постоянная.

Приближённую формулу

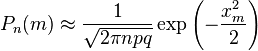
рекомендуется применять при n > 100 и npq > 20

 

Фу́нкция распределе́ния в теории вероятностей — функция, характеризующая распределение случайной величины или случайного вектора. При соблюдении известных условий (см. ниже) полностью определяет случайную величину.

Определение

Пусть дано вероятностное пространство 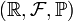, и на нём определена случайная величина 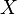с распределением . Тогда функцией распределения случайной величины 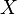называется функция 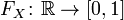, задаваемая формулой:

.

То есть функцией распределения (вероятностей) случайной величины 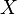называют функцию 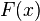, значение которой в точке 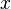равно вероятности события 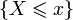, то есть события, состоящего только из тех элементарных исходов, для которых .

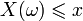Свойства

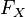· непрерывна справа:

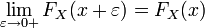
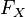· не убывает на всей числовой прямой.

· .

· .

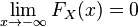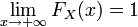· Распределение случайной величины однозначно определяет функцию распределения.

· Верно и обратное: если функция 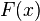удовлетворяет четырём перечисленным выше свойствам, то существует вероятностное пространство и определённая на нём случайная величина, такая что 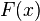является её функцией распределения.

· По определению непрерывности справа, функция 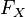имеет правый предел 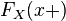в любой точке , и он совпадает со значением функции 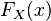в этой точке.

· В силу неубывания, функция 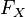также имеет и левый предел 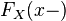в любой точке , который может не совпадать со значением функции. Таким образом, функция 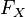либо непрерывна в точке, либо имеет в ней разрыв первого рода.