Деление многочленов
При делении многочлены представляются в канонической форме и располагаются по убывающим степеням какой-либо буквы, относительно которой определяется степень делимого и делителя. Степень делимого должна быть больше или равна степени делителя.
Результатом деления является единственная пара многочленов – частное и остаток, которые должны удовлетворять равенству:
< делимое > = < делитель > ´ < частное > + < остаток >.
Если многочлен степени n Pn(x) является делимым,
многочлен степени m Rk(x)является делителем (n ³ m),
многочлен Qn – m(x) – частное. Степень этого многочлена равна раз-ности степеней делимого и делителя,
а многочлен степени k Rk(x) является остатком (k < m).
То равенство
Pn(x) = Fm(x)× Qn – m(x) + Rk(x) (1.1)
должно выполняться тождественно, то есть, оставаться справедливым при любых действительных значениях х.
Ещё раз отметим, что степень остатка k должна быть меньше степени делителя m. Назначение остатка – дополнить произведение многочленов Fm(x) и Qn – m(x) до многочлена, равного делимому.
Если произведение многочленов Fm(x)× Qn – m(x) дает многочлен, равный делимому, то остаток R = 0. В этом случае говорят, что деление производится без остатка.
Алгоритм деления многочленов рассмотрим на конкретном примере.
Пусть требуется разделить многочлен (5х5 + х3 + 1) на многочлен (х3 + 2).
1. Разделим старший член делимого 5х5 на старший член делителя х3:
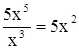 .
.
Ниже будет показано, что так находится первый член частного.
2. На очередное (поначалу первое) слагаемое частного умножается делитель и это произведение вычитается из делимого:
5х5 + х3 + 1 – 5х2(х3 + 2) = х3 – 10х2 + 1.
3. Делимое можно представить в виде
5х5 + х3 + 1 = 5х2(х3 + 2) + (х3 – 10х2 + 1). (1.2)
Если в действии (2) степень разности окажется больше или равна степени делителя (как в рассматриваемом примере), то с этой разностью действия, указанные выше, повторяются. При этом
1. Старший член разности х3 делится на старший член делителя х3:
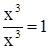 .
.
Ниже будет показано, что таким образом находится второе слагаемое в частном.
2. На очередное (теперь уже, второе) слагаемое частного умножается делитель и это произведение вычитается из последней разности
х3 – 10х2 + 1 – 1×(х3 + 2) = – 10х2 – 1.
3. Тогда, последнюю разность можно представить в виде
х3 – 10х2 + 1 = 1×(х3 + 2) + (–10х2 + 1). (1.3)
Если степень очередной разности окажется меньше степени делителя (как при повторе в действии (2)), то деление завершено с остатком, равным последней разности.
Для подтверждения того, что частное является суммой (5х2 + 1), подставим в равенство (1.2) результат преобразования многочлена х3 – 10х2 + 1 (см.(1.3)): 5х5 + х3 + 1 = 5х2(х3 + 2) + 1×(х3 + 2) + (– 10х2 – 1). Тогда, после вынесения общего множителя (х3 + 2) за скобки, получим окончательно
5х5 + х3 + 1 = (х3 + 2)(5х2 + 1) + (– 10х2 – 1).
Что, в соответствии с равенством (1.1), следует рассматривать как результат деления многочлена (5х5 + х3 + 1) на многочлен (х3 + 2) с частным (5х2 + 1) и остатком (– 10х2 – 1).
Указанные действия принято оформлять в виде схемы, которая называется «деление уголком». При этом, в записи делимого и последующих разностей желательно производить члены суммы по всем убывающим степеням аргумента без пропуска.
5х5 + 0х4 + х3 + 0х2 + 0х + 1 х3 + 2
5х5 +10х2 5х2 + 1
х3 –10х2 + 0х + 1
х3 + 2
–10х2 + 0х – 1
Мы видим, что деление многочленов сводится к последовательному повторению действий:
1) в начале алгоритма старший член делимого, в последующем, старший член очередной разности делится на старший член делителя;
2) результат деления дает очередное слагаемое в частном, на которое умножается делитель. Полученное произведение записывается под делимым или очередной разностью;
3) из верхнего многочлена вычитается нижний многочлен и, если степень полученной разности больше или равна степени делителя, то с нею повторяются действия 1, 2, 3.
Если же степень полученной разности меньше степени делителя, то деление завершено. При этом последняя разность является остатком.