Многочлен и его стандартный вид

Многочлен и его стандартный вид

Многочленом называется сумма одночленов.

Одночлены, из которых составлен многочлен, называют членами многочлена. Так членами многочлена 4x2y - 5xy + 3x -1 являются 4x2y, -5xy, 3x и -1 .

Если многочлен состоит из двух членов, то его называют двучленом, если из трех - трехчленом . Одночлен считают многочленом, состоящим из одного члена.

В многочлене 7x3y2 - 12 + 4x2y - 2y2x3 + 6 члены 7x3y2 и - 2y2x3 являются подобными слагаемыми, так как имеют одну и ту же буквенную часть. Подобными являются и слагаемые -12 и 6, не имеющие буквенной части. Подобные слагаемые в многочлене называют подобными членами многочлена, а приведение подобных слагаемых в многочлене - приведением подобных членов многочлена.

Приведем для примера подобные члены в многочлене 7x3y2 - 12 + 4x2y - 2y2x3 + 6 = 5x3y2 + 4x2y - 6 .

Многочлен называется многочленом стандартного вида, если каждый его член является одночленом стандартного вида и этот многочлен не содержит подобных слагаемых.

Любой многочлен можно привести к стандартному виду. Для этого нужно каждый его член представить в стандартном виде и привести подобные слагаемые.

Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов.

Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.

Для примера найдем степень многочлена 8x4y2 - 12 + 4x2y - 3y2x4 + 6 - 5y2x4 :

8x4y2 - 12 + 4x2y - 3y2x4 + 6 - 5y2x4 = 4x2y -6.

Заметим, что в исходный многочлен входят одночлены шестой степени, но при приведении подобных членов все они сократились, и получился многочлен третьей степени, значит и исходный многочлен имеет степень 3!
Многочлены от одной переменной

Выражение вида , где — некоторые числа и , называется многочленом степени от .

Два многочлена называются тождественно равными, если их числовые значения совпадают при всех значениях . Многочлены и тождественно равны тогда и только тогда, когда они совпадают, т.е. коэффициенты при одинаковых степенях этих многочленов одинаковы.

При делении многочлена на многочлен (например «уголком») получаем многочлен (неполное частное) и остаток — многочлен (в случае, когда остаток равен нулю, многочлен называется частным). Если — делимое, — делитель, то многочлен представим в виде . При этом сумма степеней многочленов и равна степени многочлена , а степень остатка меньше степени делителя ..

Понятие многочлена. Степень многочлена

Многочленом от переменной х будем называть выражение вида

anxn+an-1xn-1+... +a1x+a0,где n - натуральное число; аn, an-1,..., a1, a0 - любые числа, называемые коэффициентами этого многочлена. Выражения anxn, an-1xn-1,..., a1х, a0 называются членами многочлена, а0 - свободным членом.

Часто будем употреблять и такие термины: an - коэффициент при хn, аn-1 - коэффициент при хn-1 и т.д.

Примерами многочленов являются следующие выражения: 0х4+2х3+ (-3) х3+ (3/7) х+; 0х2+0х+3; 0х2+0х+0. Здесь для первого многочлена коэффициентами являются числа 0, 2, - 3, 3/7, ; при этом, например, число 2 - коэффициент при х3, а - свободный член.

Многочлен, у которого все коэффициенты равны нулю, называется нулевым.

Так, например, многочлен 0х2+0х+0 - нулевой.

Из записи многочлена видно, что он состоит из нескольких членов. Отсюда и произошел термин ‹‹многочлен›› (много членов). Иногда многочлен называют полиномом. Этот термин происходит от греческих слов πολι - много и νομχ - член.

Многочлен от одной переменной х будем обозначать так: f (x), g (x), h (x) и т.д. например, если первый приведённых выше многочленов обозначить f (x), то можно записать: f (x) =0x4+2x3+ (-3) x2+3/7x+.

Для того чтобы запись многочлена выглядела проще и выглядела компактнее, договорились о ряде условностей.

Те члены не нулевого многочлена, у коэффициенты равны нулю, не записывают. Например, вместо f (x) =0x3+3x2+0x+5 пишут: f (x) =3x2+5; вместо g (x) =0x2+0x+3 - g (x) =3. Таким образом, каждое число - это тоже многочлен. Многочлен h (x), у которого все коэффициенты равны нулю, т.е. нулевой многочлен, записывают так: h (x) =0.

Коэффициенты многочлена, не являющиеся свободным членом и равные 1, тоже не записывают. Например, многочлен f (x) =2x3+1x2+7x+1 можно записать так: f (x) =x3+x2+7x+1.

Знак ‹‹-›› отрицательного коэффициента относят к члену, содержащему этот коэффициент, т.е., например, многочлен f (x) =2x3+ (-3) x2+7x+ (-5) записывают в виде f (x) =2x3-3x2+7x-5. При этом, если коэффициент, не являющийся свободным членом, равен - 1, то знак "-" сохраняют перед соответствующим членом, а единицу не пишут. Например, если многочлен имеет вид f (x) =x3+ (-1) x2+3x+ (-1), то его можно записать так: f (x) =x3-x2+3x-1.

Может возникнуть вопрос: зачем, например, уславливаться о замене 1х на х в записи многочлена, если известно, что 1х=х для любого числа х? Дело в том, что последнее равенство имеет место, если х - число. В нашем же случае х - элемент произвольной природы. Более того запись 1х мы пока не имеем права рассматривать как произведение числа 1 и элемента х, ибо, повторяем х - это не число. Именно таким обстоятельством и вызваны условности в записи многочлена. И если мы дальше говорим все-таки о произведении, скажем, 2 и х без всяких оснований, то этим допускаем некоторую нестрогость.

В связи с условностями в записи многочлена обращаем внимание на такую деталь. Если имеется, например, многочлен f (x) =3х3-2х2-х+2, то его коэффициенты - это числа 3, - 2, - 1,2. Конечно, можно было бы сказать, что коэффициентами являются числа 0, 3, - 2, - 1, 2, имея в виду такое представление данного многочлена: f (x) =0x4-3x2-2x2-x+2.

В дальнейшем для определенности будем указывать коэффициенты, начиная с отличного от нуля, в порядке их следования в записи многочлена. Так, коэффициентами многочлена f (x) =2x5-x являются числа 2, 0, 0, 0, - 1, 0. Дело в том, что хотя, например, член с х2 в записи отсутствует, это лишь означает, что его коэффициент равен нулю. Аналогично свободного члена в записи нет, поскольку он равен нулю.

Если имеется многочлен f (x) =anxn+an-1xn-1+... +a1x+a0 и an≠0, то число n называют степенью многочлена f (x) (или говорят: f (x) - n-й степени) и пишут ст. f (x) =n. В этом случае an называется старшим коэффициентом, а anxn - старшим членом данного многочлена.

Например, если f (x) =5x4-2x+3, то ст. f (x) =4, старший коэффициент - 5, старший член - 5х4.

Рассмотрим теперь многочлен f (x) =a, где а - число, отличное от нуля. Чему равна степень этого многочлена? Легко заметить, что коэффициенты многочлена f (x) =anxn+an-1xn-1+... +a1x+a0 пронумерованы справа налево числами 0, 1, 2, …, n-1, n и если an≠0, то ст. f (x) =n. Значит, степень многочлена - это наибольший из номеров его коэффициентов, отличных от нуля (при той нумерации, о которой только что говорилось). Вернемся теперь к многочлену f (x) =a, a≠0, и пронумеруем его коэффициенты справа налево числами 0, 1, 2, … коэффициент а при этом получит номер 0, а так как все остальные коэффициенты - нулевые, то это и есть самый большой из номеров коэффициентов данного многочлена, отличных от нуля. Значит ст. f (x) =0.

Таким образом, многочлены нулевой степени - это числа, отличные от нуля.

Осталось выяснить, как обстоит дело со степенью нулевого многочлена. Как известно, все его коэффициенты равны нулю, и поэтому к нему нельзя применить данное выше определение. Так вот, условились нулевому многочлену не присваивать никакой степени, т.е. что он не имеет степени. Такая условность вызвана некоторым обстоятельством, которые будут рассмотрены несколько позже.

Итак, нулевой многочлен степени не имеет; многочлен f (x) =a, где а - число, отличное от нуля, имеет степень 0; степень же всякого другого многочлена, как легко заметить, равна наибольшему показателю степени переменной х, коэффициент при которой равен нулю.

В заключение напомним еще несколько определений. Многочлен второй степени f (x) =ax2+bx+c называется квадратным трехчленом. Многочлен первой степени вида g (x) =x+c называется линейным двучленом.
Схема Горнера.

Схема Горнера - один из простейших способов деления многочлена на бином x-a. Конечно, делением применение схемы Горнера не исчерпывается, но для начала рассмотрим именно это. Применение алгоритма поясним на примерах. Разделим на . Составим таблицу из двух строк: в первой строке запишем коэффициенты многочлена по убыванию степеней переменной. Заметьте, что данный многочлен не содержит х, т.е. коэффициент перед х равен 0. Так как мы делим на , во второй строке запишем единицу:

Начнем заполнять пустые ячейки во второй строке. В первую пустую ячейку запишем 5, просто перенеся ее из соответствующей ячейки первой строки:

Следующую ячейку заполним по такому принципу:

Аналогично заполним и четвертую: :

Для пятой ячейки получим :

И, наконец, для последней, шестой ячейки, имеем :

Задача решена, осталось только записать ответ:

Как видите, числа, расположенные во второй строке (между первым и последним), есть коэффициенты многочлена, полученного после деления на . Последнее число во второй строке означает остачу от деления или, что то же самое, значение многочлена при . Следовательно, если в нашем случае остача равна нулю, то многочлены делятся нацело.

Полученный результат говорит также и о том, что 1 является корнем многочлена .

Приведем еще один пример. Разделим многочлен на . Сразу оговорим, что выражение нужно представить в форме . В схеме Горнера будет учавствовать именно -3.

Если наша цель - найти все корни многочлена, то схему Горнера можно применять несколько раз подряд, - до тех пор, пока мы не исчерпаем все корни. Например, отыщем все корни многочлена . Целые корни нужно искать среди делителей свободного члена, т.е. среди делителей 8. Т.е., целыми корнями могут быть числа -8, -4, -2, -1, 1, 2, 4, 8. Проверим, к примеру, 1:

Итак, в остаче имеем 0, т.е. единица действительно является корнем данного мнгогочлена. Попробуем проверить единицу еще несколько раз. Новую таблицу для этого создавать не будем, а продолжим использование предыдущей:

Вновь в остаче ноль. Продолжим таблицу до тех пор, пока не исчерпаем все возможные значения корней:

Итог: Конечно, данный метод подбора малоэффективен в общем случае, когда корни не являются целыми числами, но для целых корней метод довольно-таки неплох.

РАЦИОНАЛЬНЫЕ КОРНИ МНОГОЧЛЕНА С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ Нахождение корней многочлена – интересная и достаточно трудная задача, решение которой выходит за границы школьного курса математики. Однако для многочленов с целыми коэффициентами есть простой переборный алгоритм, позволяющий находить все рациональные корни.

Теорема. Если многочлен с целыми коэффициентами имеет рациональный корень ( – несократимая дробь),

то числитель дроби является делителем свободного члена, а знаменатель – делителем старшего коэффициента этого многочлена.

Доказательство

Пусть многочлен записан в каноническом виде Подставим и освободимся от знаменателей, домножив на наибольшую степень n:

Перенесем вправо член

Произведение делится на целое число m. По условию дробь несократима, следовательно, числа m и n взаимно просты. Тогда взаимно простыми будут числа m и Если произведение чисел делится на m, а множитель взаимно прост с m, то второй множитель должен делиться на m.

Доказательство делимости старшего коэффициента на знаменатель n доказывается точно так же, перенося вправо член и вынося слева множитель n за скобку.

Сделаем несколько замечаний к доказанной теореме.

Замечания

1) Теорема дает только необходимое условие существования рационального корня. Это означает, что нужно проверить все рациональные числа, с указанным в теореме свойством и отобрать из них те, которые окажутся корнями. Других не будет.

2) Среди делителей надо брать не только положительные, но и отрицательные целые числа.

3) Если старший коэффициент равен 1, то всякий рациональный корень должен быть целым, так как у 1 нет делителей, кроме

Проиллюстрируем теорему и замечания к ней на примерах.

Примеры.

1) Рациональные корни должны быть целыми.

Перебираем делители свободного члена: Положительные числа подставлять нет смысла, так как все коэффициенты многочлена положительны и при

Осталось вычислить F(–1) и F(–2). F(–1)=1+0; F(–2)=0.

Итак, многочлен имеет один целый корень x=–2.

Можем поделить F(x) на x+2 :

2) Выписываем возможные значения корней:

Подстановкой убеждаемся, что и Многочлен имеет три различных рациональных корня:

Конечно, корень x = -1 угадывается легко. Потом можно разложить на множители и искать корни квадратного трехчлена обычными приемами.

ДЕЛЕНИЕ МНОГОЧЛЕНОВ. АЛГОРИТМ ЕВКЛИДА

Деление многочленов

Результатом деления является единственная пара многочленов – частное и остаток, которые должны удовлетворять равенству: < делимое > = < делитель > ´ < частное > + <… Если многочлен степени n Pn(x) является делимым,

Пример №1

6х³ + х² – 3х – 2 2х² – х – 1

6х³ ± 3х² ± 3х 3х + 2

4х² + 0х – 2

4х² ± 2х ± 2

2х

Таким образом, 6х³ + х² – 3х – 2 = (2х² – х – 1)( 3х + 2) + 2х.

 

Пример №2

a⁵ + b⁵ a + b

a⁵ 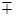a⁴b a⁴ –a³b + a²b² – ab³ + b⁴

– a⁴b + b⁵

± a⁴b ± a³b²

a³b² + b⁵

a³b² 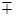a²b³

– a²b³ + b⁵

± a²b³ ± ab⁴

+ ab⁴ + b⁵

– ab⁴ 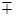b⁵

Таким образом, a⁵ + b⁵ = (a + b)(a⁴ –a³b + a²b² – ab³ + b⁴).

 

Пример №3

х⁵ – у⁵ х – у

х⁵ 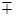х⁴у х⁴ + х³у + х²у² + ху³ + у⁴

х⁴у – у⁵

х⁴у ± х³у²

х³у² – у⁵

х³у² ± х²у³

х²у³ – у⁵

х²у³ ± ху⁴

ху⁴ – у⁵

ху⁴ – у⁵

Таким образом, х⁵ – у⁵ = (х – у)( х⁴ + х³у + х²у² + ху³ + у⁴).

Обобщением результатов, полученных в примерах 2 и 3, являются две формулы сокращенного умножения:

(х + а)(х²ⁿ – х^2n–1a + х^2n–2a² – … + a²ⁿ) = х²ⁿ⁺¹ + a^{2n + 1};

(х – a)(х²ⁿ + х^2n–1a + х^2n–2a² + … + a²ⁿ) = х²ⁿ⁺¹ – a^{2n + 1}, где nÎN.

 

Упражнения

1. (– 2х5 + х4 + 2х3 – 4х2 + 2х + 4) : (х3 + 2). Ответ: – 2х2 + х +2 – частное, 0 – остаток. 2. (х4 – 3х2 + 3х + 2) : (х – 1).

Нахождение наибольшего общего делителя двух многочленов

Алгоритм Евклида

Наибольшим общим делителем (НОД) двух многочленов называется их общий делитель наибольшей степени. Заметим, что любое число неравное нулю является общим делителем двух любых… Алгоритм Евклида предлагает последовательность действий, которая или приводит к нахождению НОД двух данных…

Пример №1

Сократить дробь .

Решение

1) х3 + 6х2 + 11х + 6 х3 + 7х2 + 14х + 8 х3 + 7х2 + 14х + 8 1 – х2 – 3х – 2

Возможности упрощения вычислений НОД в алгоритме Евклида

Теорема

При умножении делимого на число не равное нулю частное и остаток умножаются на такое же число.

Доказательство

Пусть P – делимое, F – делитель, Q – частное, R – остаток. Тогда,

P = F×Q + R.

Умножая данное тождество на число a ¹ 0, получим

aP = F×(aQ) + aR,

где многочлен aP можно рассматривать как делимое, а многочлены aQ и aR – как частное и остаток, полученные при делении многочлена aP на многочлен F. Таким образом, при умножении делимого на число a ¹ 0, частное и остаток так же умножаются на a, ч.т.д

Следствие

Умножение делителя на число a ¹ 0 можно рассматривать как умножение делимого на число .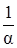

.

Следовательно, при умножении делителя на число a ¹ 0 частное и остаток умножается на .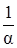

Пример №2

Найти частное Q и остаток R при делении многочленов

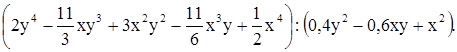
Решение

12у4 – 22ху3 + 18х2у2 – 11х3у + 3х4 2у2 – 3ху + 5х2 12у4 ± 18ху3 30х2у2 6у2 – 2ху – 9х2 = – 4ху3 – 12х2у2 – 11х3у + 3х4

Пример №3

Сократить дробь .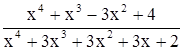

Решение

1) х4 + 3х3 + 3х2 + 3х + 2 х4 + х3 – 3х2 + 4 х4 х3 ± 3х2 4 1 2х3 + 6х2 + 3х – 2

Упражнения

1. Ответ: . 2. Ответ: 3. Ответ:

Нахождение НОД двух натуральных чисел

Пример №1

Найти НОД двух чисел 323 и 247

Решение

1) 323 247 2) 247 76 3) 76 19

247 1 228 3 76 4

76 19 0

Ответ: НОД _{323; 247} = 19.

 

Пример №2

Найти НОД двух чисел 323 и 107

Решение

321 3 100 53 2 7 1 не существует