Св-ва БМ величин

1.алгебраическая сумма конечного числа БМ величин есть величина БМ

2.произведение БМ величины на ограниченную функцию есть величина БМ

3.частное от деления БМ величины на функцию, предел который отличен от нуля, есть величины БМ.

Доказательство 1 св-ва.

Дано α(х,), β(х) – БМ

Д-ть: (α(х,)+ β(х)) – БМ при x→х₀

Док-во по усл. α(х,) есть БМ при x→х₀

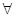Е>0

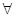Е’= Е/2>0, 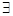σ₁>0, х≠х₀

|х- х₀|< σ₁ (1)

| α(х,) |<Е/2 (2)

По усл β(х) – БМ при x→х₀

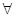Е’= Е/2>0, 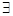σ₂>0, х≠х₀

|х- х₀|< σ₂ (3)

| β (х,) |<Е/2 (4)

σ= min (σ₁ ;σ₂)

|х- х₀|< σ (5)

Тогда значения х удовл (5) будут верны оба нер-ва

(2) и (4) складываем их и получаем

| α(х,)+ | β (х,) <Е/2+Е/2

|x+y|<|x|+|y|

По свойству модулей получим |α(х,)+ β(х) |<Е (6)

Итак, для любого Е>0 существует такое число σ>0, что для всех х≠х₀ удовл. усл.(5) будет верно нер-во (6)

 

Функция y=f(x) называется ББпри определенном стремлении аргумента, если рано или поздно ее значение по модулю будут больше любого наперед выбранного полож числа | f(x) |>M. M>0

lim f(x)=∞