Каноническое уравнение эллипса.

Теорема. В канонической для эллипса системе координат уравнение эллипса имеет вид:

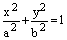. (4)

Доказательство. Доказательство проведем в два этапа. На первом этапе мы докажем, что координаты любой точки, лежащей на эллипсе удовлетворяют уравнению (4). На втором этапе мы докажем, что любоерешение уравнения (4) дает координаты точки, лежащей на эллипсе. Отсюда будет следовать, что уравнению (4) удовлетворяют те и только те точки координатной плоскости, которые лежат на эллипсе. Отсюда и изопределения уравнения кривой будет следовать, что уравнение (4) является уравнением эллипса.

Геометрический смысл параметра 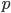- расстояние от начала координат до плоскости. Вектор нормали направлен в сторону полуплоскости, в которой нет начала координат.

 

29. Каноническое уравнение гиперболы: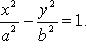

Каноническое уравнение параболы:

Уравнения асимптот: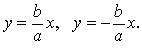

30. Общим уравнением плоскости в пространстве называется уравнение вида

Ax + By + Cz + D = 0,

где A² + B² + C² ≠ 0 .

Рассмотрим важный частный случай построения уравнения плоскости, когда известны три точки M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃), принадлежащие плоскости и не лежащие на одной прямой. Возьмем текущую точку M(x, y, z) плоскости и организуем три вектора

Эти векторы лежат в одной плоскости, уравнение которой и определяется. Следовательно, их смешанное произведение равно нулю, то есть

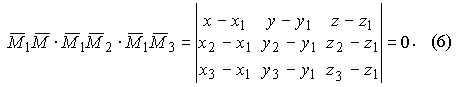
Нормальный вектор плоскости - это любой ненулевой вектор, лежащий на прямой перпендикулярной к данной плоскости.