Непрерывные случайные величины
1. Интегральная функция распределения. Для непрерывной случайной величины в отличие от дискретной нельзя построить таблицу распределения. Поэтому непрерывные случайные величины изучают другим способом, который мы сейчас рассмотрим. Пусть X — непрерывная случайная величина с возможными значениями из некоторого интервала (а; b) и х — действительное число. Под выражением Х<х понимается событие «случайная величина Л' приняла значение, меньшее х». Вероятность этого события Р(Х< х) есть некоторая функция переменной х
Р(х) = Р(Х < х).
Определение. Интегральной функцией распределения (или кратко функцией распределения) непрерывной случайной величины X называется функция F(х), равная вероятности того, что X приняла значение, меньшее х:
F(х) = Р(Х < х). (9.4)
Отметим, что функция распределения совершенно также определяется для дискретных случайных величин.
Укажем свойства, которыми обладает функция F(х).
1. 0 £ F(х) £ 1.
Это свойство следует из того, что F(х) есть вероятность.
2. F(х) — неубывающая функция, т.е. если х1< х2, то F(х}) £F(х2).
Доказательство. Предположим, что х1 <х2. Событие «X примет значение, меньшее х2» можно представить в виде суммы двух несовместимых событий: «X примет значение, меньшее х1 и «X примет значение, удовлетворяющее неравенствам х1£ Х< х2». Обозначим вероятности последних двух событий соответственно через Р(Х< х1) и Р(х1£Х<х2). По теореме о вероятности суммы двух несовместимых событий
Р(Х < х2) = Р(Х< х1) +Р(х1£Х<х2).
откуда с учетом (9.4)
Р(х1£Х<х2)= F(х2)- F(х1). (9.5)
Так как вероятность любого события есть число неотрицательное, то Р(х1£Х<х2)³0 и, значит, F(х2)³F(х1).
Формула (9.5) утверждает свойство 3.
5. Вероятность попадания случайной величины Х в полуинтервал [а; b) равна разности между значениями функции распределения в правом и левом концах интервала (а; b):
Р(а£Х<b) = F(b)-F(а). (9.6)
Пример 9.9. Случайная величина X задана функцией распределения
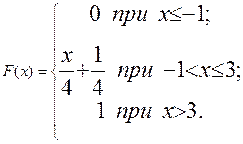
Найдем вероятности того, что в результате испытания X примет значение, принадлежащее полуинтервалу [0; 2).
х
Решение. Так как на полуинтервале [0; 2) F(х) =  то
то
Р(0£Х<2) = F(2)-F(0)= 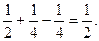
В дальнейшем случайную величину X будем называть непрерывной, если непрерывна ее функция распределения F(х) с непрерывной или кусочно-непрерывной производной.
4. Вероятность того, что непрерывная случайная величина X примет какое-либо заранее заданное значение, равна нулю:
Р(Х = х1) = 0. (9.7)
Доказательство. Положив в (9.5) х2 = х1+ Dх, будем иметь
Р(х1 £ X < х1+ Dх) = F(х1+ Dх) - F(х1 ). (9.8)
Так как F(х) — непрерывная функция, то, перейдя в (9.8) к пределу при Dх®0, получим искомое равенство (9.7). Из свойства 4 следует свойство 5.
5. Вероятности попадания непрерывной случайной величины в интервал, сегмент и полуинтервал с одними и теми же концами одинаковы
Р(a<X <b) = Р(a£ X £ b) = Р(a£ X <b) = Р(a<X £ b) . (9.9)
6. Если возможные значения случайной величины X принадлежат интервалу (а; b), то 1) F(х) = 0 при х £а; 2) F(х) = 1 при х³b.
Доказательство. 1) Пусть х1 £а. Тогда событие Х< х1 невозможно, и, следовательно, вероятность его равна нулю.
2) Пусть х2 ³ b. Тогда событие X < х2 достоверно, и, следовательно, вероятность его равна 1.
Следствие. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения:
F(-¥) = =0; F(¥) =
=0; F(¥) = == 1.
== 1.
2. Дифференциальная функция распределения. Дифференциальной функцией распределения непрерывной случайной величины ДГ(или ее плотностью вероятности) называется функция f(х) равная производной интегральной функции: f(х) =F’(х)
Так как F(х) — неубывающая функция, то f(х) ³ 0 (см. подразд. 3.7, п. 1).
Теорема 9.3. Вероятность попадания непрерывной случайной величины X в интервал (а; b) равна определенному интегралу от дифференциальной функции распределения величины X, взятому в пределах от а до b:
Р(а<Х<b)=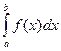 . (9.10)
. (9.10)
Доказательство. Так как F(х)является первообразной для f(х), то на основании формулы Ньютона— Лейбница (см. подразд. 4.4, п. 2)
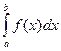 =F(b)-F(а). (9.11)
=F(b)-F(а). (9.11)
Теперь с учетом соотношений (9.6), (9.9), (9.11) получим искомое равенство.
Из (9.10) следует, что геометрически (см. подразд. 4.3, п. 2) вероятность Р(а<X<b) представляет собой площадь криволинейной трапеции, ограниченной графиком плотности вероятности у =f(х) и отрезками прямых у = 0, х = а и х = b.
Следствие.В частности, если f(х)) — четная функция и концы интервала симметричны относительно начала координат, то
Р(-а<Х<a)= Р(½Х½<a)= 2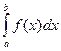 (9.12)
(9.12)
Заменяя в формуле (9.11) а на -¥ и b на х, получаем
F(x)-F(-¥)= 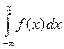 .
.
откуда, в силу найденного выше следствия (см. п. 1),
F(x)= 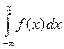 . (9.13)
. (9.13)
Формула (9.13) дает возможность отыскать интегральную функцию распределения F(x) по ее плотности вероятности.
Отметим, что из формулы (9.13) и из только что отмеченного следствия вытекает, что
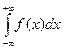 =1 (9.14)
=1 (9.14)
Пример 9.10. Задана плотность вероятности случайной величины X
f(x)=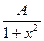 (-¥< x < +¥)
(-¥< x < +¥)
Требуется найти коэффициент А, функцию распределения F(х) и вероятность попадания случайной величины Х в интервал (0; 1).
Решение. Коэффициент А найдем, воспользовавшись соотношением (9.14). Так как
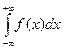 =
= =
= +
+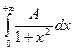 =A arctg x
=A arctg x + A arctg x
+ A arctg x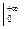 =
=
= A arctg (+¥)-A arctg (-¥)=Аp,
то Аp = 1, откуда А =1/p.
Применяя формулу (9.13), получаем функцию распределения F(х):
F(х)= 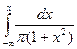 =
=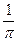 A arctg x
A arctg x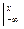 =
=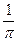 [ arctg x- arctg (-¥)]=
[ arctg x- arctg (-¥)]=
== +
+ 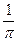 arctg x.
arctg x.
Наконец, формулы (9.6) и (9.9) с учетом найденной функции F(х) дают
P(0< x < 1)= F(1)- F(0)=  .
.