Гипергеометрическое распределение
Гипергеометрическое распределение имеет место при выборочном контроле конечной совокупности объектов объёма N по альтернативному признаку. Каждый контролируемый объект классифицируется либо как обладающий признаком A, либо как не обладающий этим признаком. Гипергеометрическое распределение имеет случайная величина Y, равная числу объектов, обладающих признаком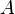 
в случайной выборке объёма 
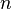, где n<N. Например, число Y дефектных единиц продукции в случайной выборке объёма 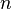из партии объёма N имеет гипергеометрическое распределение, если n<N. Другой пример — лотерея. Пусть признак A билета — это признак «быть выигрышным». Пусть всего билетов N, а некоторое лицо приобрело n из них. Тогда число выигрышных билетов у этого лица имеет гипергеометрическое распределение.
Для гипергеометрического распределения вероятность принятия случайной величиной Y значения y имеет вид
,
где D— число объектов, обладающих признаком A, в рассматриваемой совокупности объёма N. При этом y принимает значения от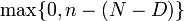 
до 
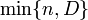, при прочих y вероятность в формуле равна нулю. Таким образом, гипергеометрическое распределение определяется тремя параметрами — объёмом генеральной совокупности N, числом объектов D в ней, обладающих рассматриваемым признаком A, и объёмом выборки .
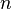Простой случайной выборкой объёма 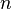из совокупности объёма N называется выборка, полученная в результате случайного отбора, при котором любой из 
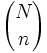наборов из n объектов имеет одну и ту же вероятность быть отобранным. Методы случайного отбора выборок респондентов (опрашиваемых) или единиц штучной продукции рассматриваются в инструктивно-методических и нормативно-технических документах. Один из методов отбора таков: объекты отбирают один из другим, причём на каждом шаге каждый из оставшихся в совокупности объектов имеет одинаковые шансы быть отобранным. В литературе для рассматриваемого типа выборок используются также термины «случайная выборка», «случайная выборка без возвращения».
Поскольку объёмы генеральной совокупности (партии) N и выборки 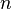обычно известны, то подлежащим оцениванию параметром гипергеометрического распределения является D. В статистических методах управления качеством продукции D — обычно число дефектных единиц продукции в партии. Представляет интерес также характеристика распределения 
— уровень дефектности.
Для гипергеометрического распределения
, 
.
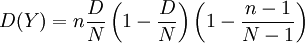Последний множитель в выражении для дисперсии близок к 1, если N>10n. Если при этом сделать замену 
, то выражения для математического ожидания и дисперсии гипергеометрического распределения перейдут в выражения для математического ожидания и дисперсии биномиального распределения. Это не случайно. Можно показать, что
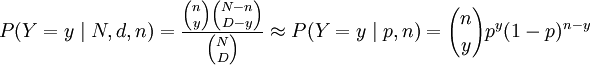, y=0, 1, 2, …, n,
при N>10n, где . Точнее, справедливо предельное соотношение
, y=0, 1, 2, …, n, и этим предельным соотношением можно пользоваться при N>10n
.
3. Распределение Пуассона.Пусть производится серия п независимых испытаний (п = 1, 2, 3, ...), причем вероятность появления данного события А в этой серии Р(А)=рn>0 зависит от ее номера п и стремится к нулю при п®¥ (последовательность «редких событий»). Предположим, что для каждой серии среднее значение числа появлений события А постоянно, т.е. п рn = m= const.
Отсюда рn = m/п.
Исходя из формулы Бернулли (9.15), для вероятности появления события А в n-й серии ровно т раз имеем выражение Рп(т) =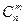 
рт(1-p)n-т=
.
Пусть т фиксировано. Тогда 
=
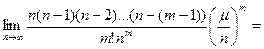
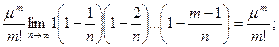
(здесь использован второй замечательный предел; см. подразд. 2.5). Поэтому
.
Если п велико, то в силу определения предела (см. подразд. 2.5) вероятность Рп(т) сколь угодно мало отличается от 
. Отсюда при больших п для искомой вероятности Рп(т) имеем приближенную формулу Пуассона (для простоты знак приближенного равенства опущен)
Рп(т) =, где m= прn.
Определение. Говорят, что случайная величина X распределена по закону Пуассона, если эта величина задана таблицей:
| X | …. | ||||
| р | 
| 
| 
| 
| …. |
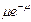
Здесь m — фиксированное положительное число (разным значениям m отвечают разные распределения Пуассона).
Найдем математическое ожидание дискретной величины X, распределенной по закону Пуассона. Согласно определению математического ожидания (см. подразд. 9.2, п. 2, примечание 2)
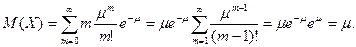
Найдем далееD(Х).Сначала найдемМ(Х2):
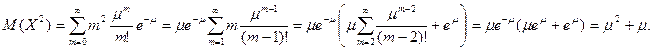Теперь по известной формуле (см. подразд. 9.3, п. 2)
D(Х)= М(Х2)- М2(Х)=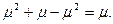
Это распределение названо в честь французского математика Симеона-Дени Пуассона (1781—1840), впервые получившего его в 1837 году.
Мы только что доказали, что распределение Пуассона является предельным случаем биномиального распределения, когда вероятность 
осуществления события мала, но число испытаний 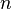велико, причём 
. Точнее, справедливо предельное соотношение
,
.
Поэтому распределение Пуассона (в старой терминологии «закон распределения») часто называют также «законом редких событий».
Распределение Пуассона возникает в теории потоков событий. Доказано, что для простейшего потока с постоянной интенсивностью 
число событий (вызовов), происшедших за время 
, имеет распределение Пуассона с параметром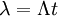 
. Следовательно, вероятность того, что за время не произойдет ни одного события, равна 
, то есть функция распределения длины промежутка между событиями является экспоненциальной.
Распределение Пуассона крайне важно во многих физических и биологических задачах. Оно представляет собой грубую модель частоты встречаемости катастрофических наводнений при довольно длительном периоде наблюдений. Распределение микроэлементов в образце почвы может также приближаться к пуассоновскому.
Распределение Пуассона используется при анализе результатов выборочных потребителей товара, расчёте оперативных характеристик планов статистического приёмочного контроля в случае малых значений приёмочного уровня дефектности, для описания числа разладок статистически управляемого технологического процесса в единицу времени, числа «требований на обслуживание», поступающих в единицу времени в систему массового обслуживания, статистических закономерностей несчастных случаев и редких заболеваний, и так далее.
Описание иных параметрических семейств дискретных распределений и возможности их практического использования рассматриваются в обширной (более миллиона названий статей и книг на десятках языков) литературе по вероятностно-статистическим методам.
5.Равномерное распределение. Распределение вероятностей непрерывной случайной величины X, принимающей все свои значения из отрезка [а; b], называется равномерным, если ее плотность вероятности на этом отрезке постоянна, а вне его равна нулю, т. е.
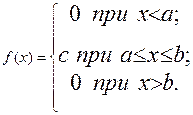
Отсюда(см, подразд. 9.4, п. 1)
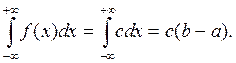(9.21)
Но, как известно (см. подразд. 9.4, п. 2),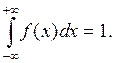 
Из сравнения этого равенства с (9.21) получаем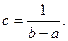 
Итак, плотность вероятности непрерывной случайной величины X, распределенной равномерно на отрезке [а; b], имеет вид
Покажем, что 
и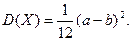
Действительно,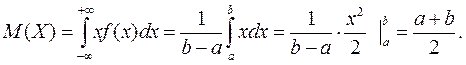 
Далее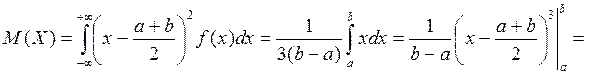
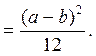
Пример 9.17. На отрезке [а; b] наугад указывают точку. Какова вероятность того, что эта точка окажется в левой половине отрезка?
Решение. Пусть X — случайная величина, равная координате выбранной точки. X распределена равномерно (в этом и состоит точный смысл слов: «наугад указывают точку»), а так как середина отрезка [а; b] имеет координату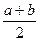 
, то искомая вероятность равна (см. подразд. 9.4, п. 2)
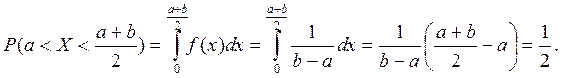
Впрочем, этот результат был ясен с самого начала.
6.Закон нормального распределения. Центральная предельная теорема.Закон распределения вероятностей непрерывной случайной величины X называется нормальным, если ее дифференциальная функция f(х) определяется формулой 
(9.22)
где параметр а совпадает с математическим ожиданием величины X: а = М(Х), параметр s является средним квадратическим отклонением величины X: s=s(X).
В подразд. 3.8 (пример 3.47) было рассмотрено построение графика функции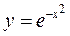 
(кривая Гаусса). С учетом графика этой функции график функции (9.22) будет иметь вид, как на рис. 9.1. Причем его максимальная ордината равна 
Значит, эта ордината убывает с возрастанием значенияs(кривая «сжимается»к оси Ох) и возрастает с убыванием значения s (кривая «растягивается» в положительном направлении оси Оy), что отражено на рис. 9.2.
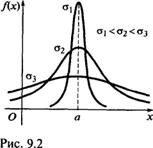Изменение значений параметра а (при неизменном значении s) не влияет на форму кривой.
Нормальное распределение с параметрами а=0 и s=1 называют нормированным. Дифференциальная функция в случае такого распределения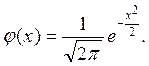 
Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу (а; b), согласно известной теореме (см. п. 2),
Сделаем в этом интеграле замену переменной, полагая 
Тогда х = =а+st, dх=s dt и
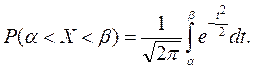(9.23)
Используя функцию (9.19), получаем
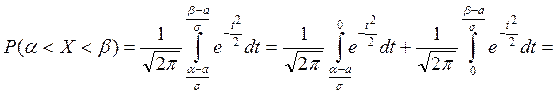
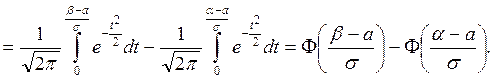
Итак,
(9.24)
Нормальное распределение вероятностей имеет в теории вероятностей большое значение. Нормальному закону подчиняется вероятность при стрельбе по цели, в измерениях и т. п.