Математическое ожидание дискретной случайной величины

1. Понятие математического ожидания.Закон распределения полностью задает дискретную случайную величину. Однако часто встречаются случаи, когда закон распределения случайной величины неизвестен. В таких случаях случайную величину изучают по ее числовым характеристикам. Одной из таких характеристик является математическое ожидание.

Пусть некоторая дискретная случайная величина X с конечным числом своих значений задана законом распределения:

xi	х1	х2	….	х n
рi	p1	p2	….	p n

Определение. Математическим ожиданием М(Х) дискретной случайной величины X называют сумму произведений всех возможных значений величины X на соответствующие вероятности:

М(Х) = х₁р₁+х₂р₂ + ... +х_n р _n. (9.1)

Пример 9.3.Используя условие примера 9.2, найдем математическое ожидание выигрыша X в примере из подразд. 9.1, п. 2.

Решение. Из полученной в примере 9.2 таблицы имеем М(Х) = 0× 0,9889 + 100×0,01 + 10000×0,001 + 100 000×0,0001 =1 + 10 + 10 = 21 р.

Очевидно, М(Х) = 21 р. есть справедливая цена одного лотерейного билета.

Теорема 9. 1. Математическое ожидание дискретной случайной величины X приближенно равно среднему арифметическому всех ее значений (при достаточно большом числе испытаний).

Доказательство. Предположим, что произведено п испытаний, в которых дискретная случайная величина X приняла значения х₁,х₂, ..., х _k соответственно m₁,m₂, ..., m_k раз, так что m₁+m₂+ ...+ m_k = п. Тогда среднее арифметическое всех значений, принятых величиной X, выразится равенством

Или .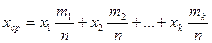

Так как коэффициент 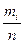является относительной частотой события «величина X приняла значение х_i (i= 1, 2, ..., k), то х_ср = х₁р^*₁+х₂р^*₂ + ... +х_n р^* _n.

Из статистического определения вероятности следует, что при достаточно большом числе испытаний р^*_i»р_i (i= 1,2,...,k). Поэтому

х_ср = х₁р₁+х₂р₂ + ... +х_n р _n.

или х_ср = М(Х).

Примечание. В связи с только что установленной теоремой математическое ожидание случайной величины называют также ее средним значением, или ожидаемым значением.