Теорема умножения для независимых событий
Для независимых событий теорема умножения
Р(АВ) = Р(А) ·РA(В)
имеет вид
Р(АВ) = Р(А) ·Р (В), (5)
т. е. вероятность совместного появления двух независимыхсобытий равна произведению вероятностей этих событий.
Подставив (4) в соотношение (3), получим
Р (A)· Р (В) = Р (В)· РB (A). (6)
Отсюда
РB(A) = Р(A),
т. е. условная вероятность события A в предположении что наступило событие В, равна его безусловной вероятности. Другими словами, событие A не зависит от события В.
Итак, если событие В не зависит от события A, то событие A не зависит от события В. Это означает, что свойство независимости событий взаимно.
Равенство (5) принимают в качестве определения независимых событий.
Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависимыми.
Вероятность произведения зависимых событий вычисляется по формуле условной вероятности.
На практике о независимости событий заключают по смыслу задачи. Например, вероятности поражения цели каждым из двух орудий не зависят от того, поразило ли цель другое орудие, поэтому события «первое орудие поразило цель» и «второе орудие поразило цель» независимы.
Замечание.Если события А и В независимы, то независимы также события
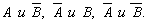
Действительно,

Следовательно,
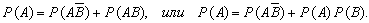
Отсюда

т. е. события А и В независимы.
Независимость событий
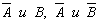
является следствием доказанного утверждения.
Несколько событий называют попарно независимыми, если каждые два из них независимы. Например, события А, В, С попарно независимы, если независимы события А и В, А и С, В и С.
Для того чтобы обобщить теорему умножения на несколько событий, введем понятие независимости событий в совокупности.
Несколько событий называют независимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных.
Например, если события A1, A2, А3, независимы в совокупности, то независимы события A1 и А2, А1 и А3, А2 и A3; А1 и A2A3, A2 и A1A3, А3 и A1A2.
Из сказанного следует, что если события независимы в совокупности, то условная вероятность появления любого события из них, вычисленная в предположении, что наступили какие-либо другие события из числа остальных, равна его безусловной вероятности.
Подчеркнем, что если несколько событий независимы попарно, то отсюда еще не следует их независимость в совокупности. В этом смысле требование независимости событий в совокупности сильнее требования их попарной независимости. Поясним сказанное на примере.
Пусть в урне имеется 4 шара, окрашенные: один — в красный цвет (А), один — в синий цвет (В), один — в черный цвет (С) и один — во все эти три цвета (АВС). Чему равна вероятность того, что извлеченный из урны шар имеет красный цвет?
Так как из четырех шаров два имеют красный цвет, то Р(А) = 2/4 = 1/2. Рассуждая аналогично, найдем Р(В) = 1/2, Р(С) = 1/ 2. Допустим теперь, что взятый шар имеет синий цвет, т. е. событие В уже произошло. Изменится ли вероятность того, что извлеченный шар имеет красный цвет, т. е. изменится ли вероятность события А? Из двух шаров, имеющих синий цвет, один шар имеет и красный цвет, поэтому вероятность события А по-прежнему равна 1/2. Другими словами, условная вероятность события А, вычисленная в предположении, что наступило событие В, равна его безусловной вероятности. Следовательно, события А и В независимы. Аналогично придем к выводу, что события A и С, В и С независимы. Итак, события А, В и С попарно независимы.
Независимы ли эти события в совокупности? Оказывается, нет. Действительно, пусть извлеченный шар имеет два цвета, например синий и черный. Чему равна вероятность того, что этот шар имеет и красный цвет? Лишь один шар окрашен во все три цвета, поэтому взятый шар имеет и красный цвет. Таким образом, допустив, что события В и С произошли, приходим к выводу, что событие А обязательно наступит. Следовательно, это событие достоверное и вероятность его равна единице. Другими словами, условная вероятность РBC(A)= 1 события А не равна его безусловной вероятности Р(А) = 1/2. Итак, попарно независимые события А, В, С не являются независимыми в совокупности.
Приведем теперь следствие из теоремы умножения.
Следствие. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
Р(А1А2 ... Аn) = Р(А1)·Р (А2) · ... ·Р(Аn).