Арифметика бесконечно малых последовательностей.
Теорема: сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Пусть 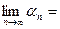
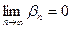 . Возьмем произвольный
. Возьмем произвольный .
.
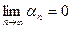


Аналогично
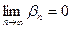

 .
.
Обозначим 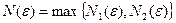 .
.
Тогда 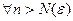
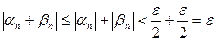 .
.
То есть 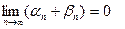
Теорема: произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.
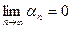 ,
,  - ограниченная, то есть
- ограниченная, то есть
 .
.
Возьмем произвольный .
.
 - бесконечно малая.
- бесконечно малая.
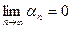
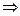

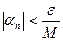 .
.
Обозначим 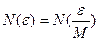 . Тогда
. Тогда
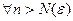
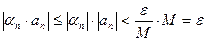 .
.
То есть
Замечание: сходимость ограниченной последовательности здесь не требуется.
БИЛЕТ 7. Теорема об арифметике пределов последовательностей.
Пусть  ,
,  . Тогда:
. Тогда:
1) существует 
2) существует 
3) если 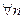
 то существует
то существует  .
.
Доказательства:

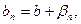 где
где  и
и  - бесконечно малые последовательности.
- бесконечно малые последовательности.
1) 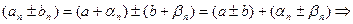

бесконечно малые.
 бесконечно малые.
бесконечно малые.

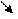
 2)
2) =
=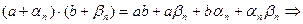

бесконечно малая бесконечно малая
бесконечно малая
3)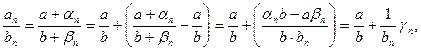 где
где
 - бесконечно малая последовательность.
- бесконечно малая последовательность.
По условию 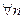


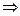
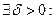

 -ограниченная.
-ограниченная.
 бесконечно малая.
бесконечно малая.
 .
.
БИЛЕТ 8. Бесконечно большие последовательности.
Определение:  бесконечно большая последовательность при
бесконечно большая последовательность при 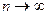 (
( ), если
), если 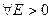
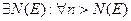 .
.  .
.
Теорема. Пусть 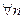
 , тогда
, тогда  бесконечно большая
бесконечно большая 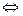
 бесконечно малая.
бесконечно малая.
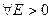

 ,
,  .
.
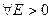

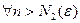 ,
, 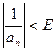
Определение: 
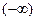
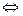
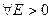
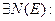

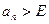 . (
. (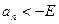 )
)
БИЛЕТ 9. Монотонные последовательности. Теорема о пределе
монотонной последовательности.
Определение: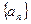 -монотонно возрастающая (монотонно убывающая),
-монотонно возрастающая (монотонно убывающая),
если 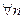
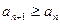 (
( ). Если неравенства строгие, то
). Если неравенства строгие, то
последовательности строго возрастающие (убывающие).
Теорема (о пределе монотонной последовательности).Пусть 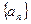
-монотонно возрастает и ограничена сверху. Тогда она сходится, причем
 .
.
Доказательство:
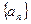 ограничена сверху =>по теореме существования точной верхней
ограничена сверху =>по теореме существования точной верхней
грани 
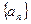 . Докажем, что
. Докажем, что 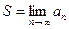 .
.
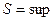
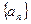 : 1)
: 1)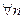

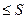
2) 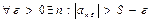 .
.
Возьмем произвольный  , обозначим
, обозначим 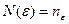 из 2).
из 2).
 1)=>
1)=> 
2)=> 
 (монот. возр).
(монот. возр).
Из этого следует, что  ,
,  =>
=>

 .
.
Мы доказали достаточное условие числовой сходимости
последовательности (монот. и огр.)
 (огр. на б.м.).
(огр. на б.м.).
БИЛЕТ 10. Число е.
Сложно доказать, что функция 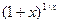 при
при 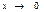
имеет предел. Этот предел обозначается буквой  в честь открывшего
в честь открывшего
его петербургского математика Леонарда Эйлера. Установлено, что
это- иррациональное число и что  =2,718281828459…. Формула,
=2,718281828459…. Формула,
определяющая число  по традиции называется второй замечательный
по традиции называется второй замечательный
предел. 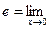
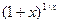 . Также число
. Также число -основание
-основание
натуральных логарифмов.
Рассмотрим  .
.