Пересечение прямой и поверхности.
(Повторение и продолжение).
 Для контроля усвоения материала хочу предложить выполнить самостоятельно две простые задачи на пересечение прямых частного положения с поверхностями конуса и цилиндра.
Для контроля усвоения материала хочу предложить выполнить самостоятельно две простые задачи на пересечение прямых частного положения с поверхностями конуса и цилиндра.
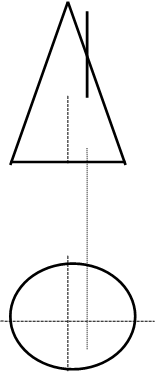 | |||
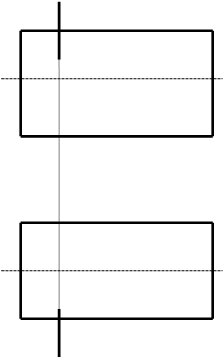 | |||
Чтобы построить точки пересечения прямой с конической или цилиндрической поверхностью, следует заключить прямую в плоскость, проходящую через вершину поверхности (собственную или несобственную), найти линию пересечения плоскости и поверхности, а затем точки , в которых эти линии пересекаются с заданной прямой.
ПЕРЕСЕЧЕНИЕ КРИВОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ.
Рассмотрим на примере пересечения кривой линии с поверхностью конуса.
На фронтальной проекции видно, что кривая L не может пересечь поверхность конуса с вершиной S левее точки А2 и правее В2.
Глядя на горизонтальную проекцию можно утверждать , что пересечение может находится в пределах ограниченных точками С 1 и D 1.
Определим как горизонтальные так и фронтальные проекции этих точек и рассмотрев их станем утверждать, что пересечение происходит между точками А и D. Если кто затрудняется прийти к такому выводу, то задавайте вопрос и я дополнительно поясню.
Далее воспользуемся дополнительным центральным проецированием.
Спроецируем коническую поверхность конуса S и кривую в пределах
АD на плоскость Т.



























S 2
Т2
Проекцией поверхности будет окружность, а проекцией кривой кривая со штрихом. ,то линии пересекаются в точках К и М.
Найдем горизонтальные проекции точек К и М .Соединив их с вершиной S получим горизонтальные проекции точек пересечения кривой с поверхностью. Найдем на фронтальной проекции этой кривой. соответствующие проекции точек пересечения.
. .
.
.
.
.
.
Метрическая задача.
Задача очень простая. Мы сможем решить ее различными известными нам
методами. Я покажу вам решение самым первым методом - треугольника.
Вы же попробуйте получить решение заменой плоскости проекций и методом
вращения.
Построить основной чертеж сферы с центром в точке С, если точка А
принадлежит ее поверхности.
 А 2 ·
А 2 ·
.
 . · С 2
. · С 2
· С1
· А1
Задача сводится к нахождению натуральной величины отрезка АС.
Если мы возьмем превышение по оси Z токи А2 над тоской С2 и отложим его под
прямым углом к проекции А1С1, то диагональ полученного прямоугольного
треугольника будет равна натуральной величине отрезка или радиусу сферы.