рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Вид работы: Лекции
- /
- Введение в курс. Курс лекций Начертательная геометрия
Реферат Курсовая Конспект
Введение в курс. Курс лекций Начертательная геометрия
Введение в курс. Курс лекций Начертательная геометрия - Лекция, раздел Математика, Введение В Курс. Курс Лекц...
Введение в курс.
Курс лекций Начертательная геометрияв которой рассматриваются следующие основные вопросы :
1) Построение изображений или чертежей предметов;
2) Решение геометрических задач в пространстве при помощи чертежей на плоскости.
Начертательная геометрия является лучшим средством развития у человека пространственного воображения, без которого не мыслимо инженерное творчество.
Основы этой науки заложены были при разработке первых чертежей. Дошедшие до нас чертежи и рисунки Древней Руси говорят о том, что при их создании применялись методы близкие к геометрическим методам. Древние памятники инженерной графики свидетельствуют, что графическое искусство на Руси было на высоком уровне.
Научное обоснование методов начертательной геометрии произошло в семнадцатом веке в связи с начавшемся бурным развитием в Европе промышленности. Основоположником считается видный французский ученый и политический деятель Гаспар Монж (1746 - 1818 гг.). Его учение о ортогональном методе проецированная сохранилось до нашего времени .
В России начертательную геометрию впервые стали изучать с 1810 года в Институте корпуса инженеров путей сообщения (С-Петербург), а с 1830 года стали преподавать во всех высших учебных заведениях России.
Первым русским ученым издавшим труд “Основания начертательной геометрии “ в 1821 году был профессор Р.А. Севастьянов.
Для изучения Начертательной геометрии в Московском автомобильно-дорожном институте студентами специальности ........................... можно рекомендовать следующие учебники и учебные пособия :
1) Кузнецов Н.С. Начертательная геометрия. М. “Высшая школа”,1969, 496 с.
2) Рыжов Н.Н. Главные позиционные задачи . Методические указания по курсу начертательной геометрии. М., МАДИ., 32 с.
3) Н.Н. Рыжов, О.А. Оганесов Задание поверхностей на комплексном чертеже (Методические указания к выполнению самостоятельной работы №1), МАДИ, Москва., 1990, 34 с.
4) Фролов С.А. Начертательная геометрия. М. “Машиностроение”, 1978, 240 с.
5) Луговой М.А., Ляшкевич П.А. , Оганесов О.А. , Фамин Л.Б. Тетрадь по начертательной геометрии для студентов специальностей ДМ, КМ, ТВ, ТУ, АП, ОД. М. 1995 г.
Обозначения и символика. Знакокодовая система обозначений.
Для обозначения геометрических фигур, их проекций , для краткой записи геометрических предложений , алгоритмов решения задач используется геометрический язык составленный из символов принятых в курсе математики.
Этот язык будет изучаться последовательно по мере изложения данного курса начертательной геометрии. Литература № 4 , с. 6 - 11. Знакокодовая система обозначений приведена в приложении 1 к данному конспекту лекций.
Метод проецирования .
Исходя из различных методов изображения начертательная геометрия содержит четыре основных раздела :
- ортогональные проекции;
- проекции с числовыми отметками;
- аксонометрические проекции;
- перспективные проекции.
Ортогональный метод проецирования.
Рассмотрим это на примере проекции точки на плоскость, но предварительно зададимся плоскостями проекций : горизонтальнойП 1, фронтальной П 2 и профильной П3.Y ko
Биссектрису ОАо называют постоянной прямой ko эпюра Монжа.
Эта биссектриса позволяет установить связь между горизонтальной и профильными проекциями точки. Эта связь может быть установлена с помощью дуги окружности с центром в точке пересечения координатных осей.
Таким образом все проекции точки на комплексном чертеже находятся в проекционной связи.
Прямые соединяющие проекции точки меду собой называются линиями проекционной связи (А1,А2 или А2,А3).
Мы рассмотрели как зафиксировать положение точки в пространстве и отобразить это на комплексном чертеже. Точка относится к нульмерным геометрическим образам, не имеет измерений и не является материальной. На следующей лекции мы рассмотрим одномерные геометрические образы к которым относятся линии.
Линия имеет измерение вдоль, но не имеет толщины. При измерении длинны линии нам иногда потребуется вводить дополнительную плоскость проекций (в дополнение к уже рассмотренным : горизонтальной П1, фронтальной П2, профильной П3).
Ведение новой плоскости проекций
П2А1
П1Х1,4
 Y
Y
Новая ось проекций Х 1,4 получена при пересечении горизонтальной плоскости П1 и новой плоскости П4. Проекция А4 получена методом ортогонального проецирования.
Теперь развернем наш рисунок в комплексный чертеж вращая плоскость П1 вокруг оси Х1,2 до совмещения с плоскостью П2. При этом плоскость П4 вращается вместе с плоскостью П1.
 |
П2


 ZA *А2
ZA *А2
 |
Ах (1,2)ZA




 Х (1,2) *
Х (1,2) *
 * А4
* А4
.


 Ах1,4П 4
Ах1,4П 4
90 град.
* А1
 П 1 Х(1,4)
П 1 Х(1,4)
Новая ось проекций Х (1,4 ) определяет новое направление линии проекционной связи.
Для построения на чертеже новой проекции точки А 4 необходимо через горизонтальную проекцию точки А 1 провести линию проекционной связи перпендикулярно оси Х (1,4) и от оси Х (1,4 ) вдоль линии проекционной связи отложить расстояние , равное расстоянию от точки Адо плоскостиП 1.Это расстояние измеряем на фронтальной плоскости проекций от оси Х(1,2 ) до проекции точки А 2.





 Запишем : А, А1 = A x(1,2), А2 = А х (1,4), А 4
Запишем : А, А1 = A x(1,2), А2 = А х (1,4), А 4
Такое построение нового изображения по двум исходным называется преобразованием комплексного чертежа. В данном случае преобразование было проведено способом введения новой плоскости проекций.
Проведем еще одно преобразование чертежа при этом записав алгоритм построения с помощью знакокодовой системы обозначений. Для этого воспользуемся тем же чертежом удалив только линии символически изображавшие плоскости проекций . Здесь и в дальнейшем договоримся - то что высше оси Х (1,2) фронтальная плоскость и все, что ей принадлежит , то что ниже оси Х (1,2) горизонтальная плоскость и все, что принадлежит ей. Аналогично, ниже оси Х (1,4) горизонтальная плоскость, а высше новая плоскость П 4.
 ZA ·А2
ZA ·А2
 |
П2 Ах (1,2)ZA




 Х (1,2) *
Х (1,2) *

 П 1 · · · А 5
П 1 · · · А 5
А4 Ах (4,5)
 . Ý
. Ý

 Ах (1,4)
Ах (1,4)
90 град. П 4 П 5
 · А1 Х (4,5)
· А1 Х (4,5)
П 1 П 4
Х(1,4)
Þ
Зададим еще одну плоскость проекций П 5 перпендикулярную плоскости П 4.
На чертеже новое поле проекций задаст новая ось Х (4,5).
Чтобы получить проекцию точки А 5 на плоскости П 5 выполним следующие построения:
1) é (А 4, А 5) É А 4 ; (А4, А 5) ^ Х (4,5) .
2 ) é А 5 Ì (А 4, А5); êА х (4,5), А 5 ê = ê А х ( 1,4 ) , А 1 ê.
Расшифруем эту запись : 1) Построить прямую определяемую точками А 4, А 5 проходящую через точку А 4 ; прямая А 4 , А 5 перпендикулярна оси Х (4 ,5).
2) Построить точку А 5 принадлежащую прямой А 4, А 5 ; длина отрезка А х (4,5), А 5 равна длине отрезка А х (1,4), А 1.
Произведем эти построения на чертеже.
В качестве дополнительной литературы предлагаю использовать учебное пособие М. А. Луговой Точка, прямая, плоскость. М. МАДИ, 1995 г.
Самостоятельно в тетради по начертательной геометрии ( Л. 5) решить задачи с 1 по 5 .
Линия .
Пространственные кривые лини
В начертательной геометрии кривую линию часто рассматривают как траекторию описанную движущейся точкой. Кривая линия может быть плоской или… Из пространственных кривых в технике находят широкое применение винтовые… Если на поверхности прямого кругового цилиндра карандашом зафиксировать точку , а затем начать вращать цилиндр,…Плоские кривые линии.
Эти кривые иногда рассматривают как плоские сечения поверхностей - “конические сечения”. Рассмотрим три простейших канонических формы : эллипс, гиперболу и параболу. … Зададимся конической поверхностью.Прямая линия и ее задание на комплексном чертеже.
Прямая линия - это простейший представитель семейства линий.
На комплексном чертеже прямая линия может быть задана непосредственно своими проекциями, проекциями двух точек принадлежащих прямой или следами.
При ортогональном проецировании на плоскость, не перпендикулярную ей, прямая проецируется в прямую линию.
Чтобы спроецировать отрезок прямой линии АВ на плоскость, из крайних точек отрезка опускают перпендикуляры на плоскость проекций и полученные проекции точек А1 и В 1 соединяют прямой которяй и будет проекцией данного отрезка.


 Z
Z
П 2 В 2










 Т В
Т В
А2




 А 1290
А 1290


 1
1




 Х Ах В х
Х Ах В х

 А1 90
А1 90
 |
 В 1 П 1
В 1 П 1
 |
Y
Одна проекция прямой не определяет ее положение в пространстве, так как может соответствовать множеству прямых расположенных в этой же проецирующей плоскости .
Необходимо иметь не менее двух проекций отрезка прямой, чтобы определить положение прямой в пространстве.
Отрезок АВ наклонен ко всем плоскостям проекций, поэтому проекции отрезка будут меньше его самого. Прямая наклоненная ко всем плоскостям проекций , называется прямой общего положения.
Рассмотрим прямоугольный треугольник D АВ1. Горизонтальная проекция
çА 1, В 1ç будет равна катету А,1 этого треугольника.
Чтобы определить величину второго катета В, 1 посмотрим на фронтальную плоскость проекций. Проекция на фронтальную плоскость В 2, 1 2 равна натуральной величине второго катета В, 1. Мы в этом дополнительно убедимся когда рассмотрим частное положение прямых в пространстве. Сейчас забегая вперед, я хочу обратить ваше внимание, что катет В,1 перпендикулярен горизонтальной плоскости проекций и параллелен фронтальной плоскости проекций.
Таким образом, зная два катета прямоугольного треугольника, мы можем найти его гипотенузу. Имея комплексный чертеж прямой общего пложения, где ни одна из проекций отрезка этой прямой не равна натуральной величине отрезка , мы всё
же можем найти его натуральную величину.
В 2


 )
)

 А 2 1 2
А 2 1 2
 Х А х
Х А х
 А 1
А 1

 Аоa
Аоa


90 град В 1
Ü
В о
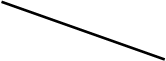
Если мы имеем чертеж с изображением отрезка в двух проекциях, то имеются все геометрические элементы для определения натуральной величины отрезка. Восстановим перпендикуляр к проекции А 1В 1 и на нем отложим расстояние равное В 2 1 2. Полученную точку В о соединим с горизонтальной проекцией А 1 точки А. Полученная гипотенуза будет натуральной величиной отрезка прямой АВ, а угол a будет натуральным углом наклона данного отрезка к горизонтальной плоскости проекций.
Без нахождения натуральной длинны отрезка нельзя найти угол наклона прямой к плоскости проекций . Поэтому если требуется найти углы наклона прямой ко всем плоскостям проекций (П 1, П2, П 3) , то необходимо определить натуральную длину отрезка на всех плоскостях проекций.
При подготовке к практическому занятию решите этим методом задачу 9 из Тетради.
Рассмотрим частные случаи расположения прямой в пространстве относительно плоскостей проекций.
Прямые уровня.
Пряма параллельная горизонтальной плоскости проекций называется горизонтальной прямой уровня или горизонталью и обозначается h. Все точки этой прямой находятся на одинаковом расстоянии от горизонтальной… ê А 1В 1ê= ê А ,В ê, êb 1 ê=êb ê; -угол наклона горизонтали к…Проецирующие прямые.
Прямая , перпендикулярная горизонтальной плоскости проекций , является горизонтально-проецирующей прямой. Отрезок этой прямой АВ.Деление отрезка в заданном отношении.
Точка принадлежащая отрезку прямой, делит его в таком же отношении, что и проекция данной точки делит проекцию отрезка.
На основании указанного свойства задача на деление отрезка в заданном отношении решается путем деления в этом отношении любой проекции отрезка. Знание этого свойства потребуется вам при решении задачи № 8 в Тетради.
Взаимное положение прямых в пространстве.
Рассмотрим взаимное положение прямых в пространстве : параллельные прямые,
пересекающиеся и скрещивающиеся.
Параллельные прямые.
Параллельные прямые имеют параллельные одноименные проекции. Обычно по двум проекциям пары прямых можно сделать заключение о их параллельности, однако если эти две прямые параллельны профильной плоскости проекций , то без…Пересекающиеся прямые.
Линии пересекающиеся в пространстве проектируются в виде пересекающихся проекций, причем проекции точки пересечения будут лежать на одной линии… К 2 a 2Скрещивающиеся прямые.
Это прямые не параллельные и не пресекающиеся между собой. Эти прямые не имеют общей точки и не лежат в одной плоскости. 12Проецирование прямого угла.
Прямой угол между двумя пресекающимися прямыми проецируется в натуральный размер только в том случае , когда одна из сторон угла параллельна… ной плоскости проекций , то прямой угол будет проецироваться в натуральный размер на фронтальную плоскость проекций.Преобразование комплексного чертежа .
Преобразование чертежа используется при решении задач связанных с измерениями… Сформулируем две первые основные задачи :Рассмотрим решение второй основной задачи преобразования чертежа
Изобразим на чертеже горизонталь h. Необходимо ввести новую плоскость проекций так, чтобы по отношению к ней… Так как данная прямая параллельна горизонтальной плоскости проекций , тоПлоскость, линии и точки в плоскости.
Проецирование элементов, определяющих плоскость.
В2 · А2 В2С1
Плоскости бывают общего положения и частного. Выше на рисунках приведены примеры плоскостей общего положения.
Плоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Плоскость частного положения параллельна или перпендикулярна хотябы к одной из плоскостей проекций . Плоскости частного положения делятся на две группы :
плоскости уровня - перпендикулярные двум плоскостям проекций и параллельные одной из них ;
проецирующие - перпендикулярные к одной плоскости проекций и наклонные к двум другим.
Плоскости уровня могут находиться в трех положениях :
1) параллельна горизонтальной плоскости проекций и перпендикулярна фронтальной и профильной;

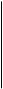

 А2 В2 С2
А2 В2 С2



 Х
Х
С1
А1
В1
2) параллельна фронтальной плоскости и перпендикулярна горизонтальной и профильной; В2
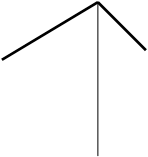

 А2 С2
А2 С2
 |

 Х
Х
А1 В1 С1
3) параллельна профильной плоскости проекций и перпендикулярна горизонтальной и фронтальной плоскостям проекций:
 |
А2 А3


 В2 В3
В2 В3

 С2
С2
С3






С1
А1
В1
Прецирующие плоскости также могут находиться в трех положениях :
1) перпендикулярна горизонтальной плоскости проекций и наклона к фронтальной и профильной плоскостям:
 В2 В3
В2 В3








 1)В22)В2 3)
1)В22)В2 3)


 С2 А2 b А3
С2 А2 b А3







 А2 А2 a
А2 А2 a





 С2 a С 2 Сз
С2 a С 2 Сз
 |  | ||||
 | |||||










 В1
В1
А1 b В1
А1 А1
В1
С1
С1 С1
2) перпендикулярна фронтальной плоскости проекций и наклона к горизонтальной и профильной плоскостям.
3) перпендикулярна профильной плоскости проекций и наклона к горизонтальной и фронтальной плоскостям.
Углы между проецирующей плоскостью и не перпендикулярными ей плоскостями проекций проецируются в натуральную величину на ту плоскость проекций , которой перпендикулярна данная плоскость.
Плоскости уровня и проектирующиеся плоскости характерны тем, что проекции всех точек и линий лежащих в этих плоскостях , будут лежать на проекции этой плоскости, которая изображается прямой линией.
Рассмотрим ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ.
Среди линий принадлежащих плоскости можно выделить линии параллельные плоскостям проекций : горизонтали плоскости, фронтали плоскости, профильные прямые плоскости. К особым относится и линия наклона, которая определяет угол наклона плоскости к той или иной плоскости проекций.
Линию наклона к плоскости П1 принято называть линией ската. Линия наклона к плоскости П2 перпендикулярна к фронталям плоскости, линия ската перпендикулярна к горизонталям плоскости, а линия наклона к плоскости П3 перпендикулярна к профильным прямым плоскости.
Условием принадлежности прямой плоскости будет:
если две точки прямой принадлежат плоскости, то и все точки данной прямой будут лежать в этой плоскости.
Т.е., чтобы начертить прямую лежащую в плоскости, достаточно найти две общие точки.
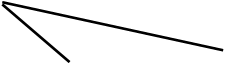
Проведем горизонталь в плоскости заданной отсеком:
Пространственный алгоритм: é h Ì D ABC )
Мы знаем, что фронтальная проекция горизонтали параллельна оси Х, вместе с тем горизонталь принадлежит плоскости заданной треугольником АВС.
Проведем через точку А 2 линию параллельную оси Х и отметим пересечение этой линии со стороной В2С2 точкой 1 2 .
( ГА: é h 2 Ç D А2В2С2) ; h 2 êê C) (Построить фронтальную проекцию горизонтали пересекающую треугольник А2В2С2; фронтальная проекция горизонтали параллельна оси Х).
Проведем линию проекционной связи для нахождения проекции 1 1.
é11Ì êB1С1÷ Ù (12 11) (Построить точку 11 принадлежащую отрезку В1С1 и линии проекционной связи 1 21 1.
В 2

 1 2
1 2



 А2 h2
А2 h2
 |
С 2
Х


 А 1 В1
А 1 В1
h1
11
С 1
é (А1 11) É А1 Ù 11
(Построить линию А1 11 включающую точки А1 и 11).
Эта линия будет горизонтальной проекцией горизонтали.
Если бы плоскость была бы задана при помощи трех
точек не лежащих на одной прямой и надо было бы провести горизонталь плоскости, задача мало бы отличалась от уже рассмотренной. Аналогично, если плоскость задана двумя пересекающимися прямыми. Любые две стороны нашего треугольника АВС можно рассматривать как пересекающиеся прямые.
Рассмотрим случай построения фронтали плоскости, если плоскость
задана двумя параллельными прямыми.
Воспользуемся тем, что нам известно направление горизонтальной
проекции фронтали. Возьмем произвольную точку 11 на прямой a1и
проведем линию параллельно оси Х до пересечения в точке21 с прямой b1.
Воспользовавшись линиями проекционной связи найдем точки 12 и 22
через которые проходит фронтальная проекция фронтали и проведем ее.
22 



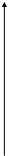 a2 f 2
a2 f 2
 12
12
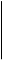 b2
b2
 Х
Х
 b 1
b 1
11 f 1 21

a 1
Точка в плоскости.
Пусть плоскость задана пересекающимися прямыми а и b. Имеется горизонтальная проекция точки А1 необходимо построить А2.B 2
B 1
*А1
A1 1 1 21
Через горизонтальную проекцию точкиа1 проведем произвольную прямую пересекающую горизонтальные проекции линий задающих плоскость
в точках 1 1 и 2 1. Построим фронтальную проекцию этой линии и на ней найдем точку а 2.
Подумайте самостоятельно, как бы мы решали аналогичную задачу, если бы были заданы обе проекции точки А и требовалось определить принадлежит ли точка А плоскости заданной пересекающимися прямыми.
Дома самостоятельно, на листе в клетку в тетради для конспектов построить эллипс. Большую и малые оси задать произвольно. Прошу не строить овал вместо эллипса.
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ
Прямая параллельная плоскости.
Если прямая АВ параллельна прямой лежащей в некоторой плоскости, то она параллельна этой плоскости. Если необходимо через заданную точку провести прямую параллельную заданной… Например, плоскость задана отсеком АВС и надо провести параллельную плоскости прямую через точку К.Параллельные плоскости.
Поэтому, если требуется через точку Dпровести плоскость параллельную заданной АВС, то через точку проводят две прямые, параллельные любым прямым,… В2В1
Пересекающиеся плоскости.
Если плоскости не параллельны, то они обязательно пересекутся. Если плоскости занимают частное положение в пространстве, то положение линии… Например, подумайте какое положение в пространстве займет линия пересечения двух горизонтально проецирующих плоскостей…ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПЛОСКОСТЬЮ.
Если прямая не параллельна плоскости, то она пересекает ее под тем или иным углом.
Алгоритм или план решения таких задач будет следующий. 1) Заключаем отрезок прямой во вспомогательную проецирующую плоскость и… 2) Находим точку пересечения отрезка прямой с линией пересечения плоскостей, которая будет искомой точкой пересечения…ПРЯМАЯ ПЕРПЕНДИКУЛЯРНАЯ ПЛОСКОСТИ
Для того, чтобы прямая была перпендикулярна плоскости, она должна быть перпендикулярна по крайней мере двум прямым, лежащим в плоскости и не параллельным друг другу.
Прямой угол проецируется в натуральный размер только в том случае, когда одна его сторона параллельна плоскости проекций. (СМ прошлую лекцию).
Поэтому достаточно в плоскости провести горизонталь и фронталь и к ним восстановить перпендикуляр, так как эти прямые проведенные из одной точки задают плоскость.
Для того чтобы восстановить перпендикуляр к плоскости, необходимо, чтобы его горизонтальная проекция была перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция фронтальной проекции фронтали.
Горизонтали и фронтали плоскости служат для определения направления проекций перпендикуляра к плоскости.
Если необходимо найти точку пересечения перпендикуляра с плоскостью, то СМ задачу на пересечение прямой с плоскостью.
22Эпюр поверхности. Изображая поверхность в ортогональных проекциях, обычно строят эпюр тех линий или точек , которые определяют единственно возможную форму поверхности.
Рассмотрим представителей семейства линейчатых поверхностей.
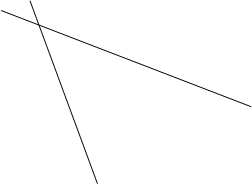
Линейчатая поверхность вполне определена, если известны три ее направляющие. Однако, в некоторых случаях достаточно знать расположение только одной направляющей и вершины.
Зададим неподвижную точку S (вершину) и направляющую k по которой скользит образующая b.
 |
 · S
· S
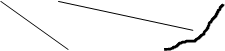 |
b k
A

Положение образующей b проходящей через точку А , как и через любую другую точку направляющей k однозначно задает поверхность. В данном случае коническую.
На эпюре коническая поверхность может быть задана так
Формула поверхности F{î (S,k) (îi É S, îi Ç k) ý

 · S 2
· S 2
b 2
A2



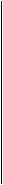 к2
к2
 · S 1
· S 1
b 1
 |
к1
S1 -A1 горизонтальная проекция
A1 построенной произвольной
образующей конической поверхности.
Если направляющая представляет собой ломаную линию, то поверхность становится пирамидальной и относится к гранным линейчатым поверхностям.
 |






 S
S
 |
b
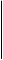

 A k
A k
На практике редко приходится изображать коническую или пирамидальную поверхность. Гораздо чаще изображают тела - конус или пирамиду.
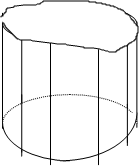
Если вершина поверхности удалена в бесконечность, то все образующие пересекающиеся с направляющей параллельны друг-другу. Когда направляющая кривая линия - поверхность носит название цилиндрической, а когда она ломаная, то поверхность будет призматической. Таким образом цилиндрическая поверхность это частный случай конической поверхности, а призматическая поверхность частный случай пирамидальной.
 | |||
 | |||
На эпюре цилиндрическая поверхность может быть задана так
 |
î2
 |
u2
 А2
А2

u1 î1
А 1
Формула поверхности F íî (î, u ;î Ç u ) (îi ççî, îi Ç u )ý.
Линейчатые поверхности с двумя направляющими
И плоскостью параллелизма.
В качестве примера рассмотрим построение гиперболического параболоида, который в технике часто называют косой плоскостью. Формула поверхности F{î( a, b, S) ( îi Ç a, b; îi÷÷ S)ý.Винтовые поверхности.
Винтовой поверхностью называется поверхность, которая описывается образующей при ее винтовом движении. Образующие могут быть как кривыми так и прямыми линиями. Прямые линии обычно называются винтовыми параллелями.В 2
a
А”2
А2
j

 А 1 jBjjjjj j , В1,В”2
А 1 jBjjjjj j , В1,В”2
A”1
Этот геликоид задан винтовой линией , шагом, диаметром, осью винтовой поверхности и образующей наклоненной к оси под углом a .
Для построения витка геликоида выполним следующие построения.
Разделим горизонтальную проекцию винтовой линии на 8 частей.
Когда точка А перемещаясь по винтовой линии перейдет в порложение А” повернувшись на 1/8 оборота, точка В переместиться по оси в положение В”. Последовательно перемещая точку А по винтовой линии и соединяя ее с положением точки В на оси прямыми линиями получим каркас винтовой поверхности.
Посторения прошу зарисовать с доски в аудитории.
Косой открытый геликоид.
Пусть в первоначальном положении образующая АВ паралельна пфронтальной плоскости проекций (П2). В точке А образующая пересекается с винтовой… Через какую бы точку образующей не проходила вторая направляющая , кратчайшее растояние между образующей и осью…В1

Для построения эпюра геликоида большая окружность на плоскости П1 разделина на 8 частей, начиная от точки А1, на то же число частей разделена внутренняя меньшая окружность начиная от точки В1.
Описанным ране приемом сторим фронтальные проекцииобеих винтовых линий.
Пересечение поверхностей геометрических тел
Плоскостями.
Сечение гранных тел проецирующими плоскостями.
Рассмотрим чертеж шестиугольной призмы рассеченной фронтально проецирующей плоскостью å. Как уже отмечалось, фронтальная проекция сечения… å 2Сечение тел вращения.
Треугольник - если секущая плоскость пересекает конус через вершину по двум образующим. Окружность - если плоскость пересекает конус параллельно основанию… Эллипс - если плоскость пересекает все образующие под некоторым углом.Пересечение поверхностей геометрических тел
Плоскостями.
Сечение гранных тел плоскостью общего положения
Геометрическое тело - трехгранная призма. А2H 2 В2
 |





 1 2
1 2
 Х1,2
Х1,2

 f 1
f 1
 1 1 3 1
1 1 3 1
 |

 h1 2 1
h1 2 1
 А1
А1
С1
 |
 В 1 3 4
В 1 3 4

 1 4
1 4


 В 4
В 4
Х 1,4 А4 C4
Построить фигуру сечения можно используя различные, уже известные нам методы. Применим метод замены плоскостей проекций. Выберем новую ось Х1,4 так, чтобы она была перпендикулярна к горизонтальной проекции горизонтали. Тогда горизонталь на…ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
ГЕОМЕТРИЧЕСКИХ ТЕЛ
1) способом вспомогательных секущих плоскостей, 2) способом сфер или вспомогательных шаровых поверхностей.Т3


 Т2
Т2





 ·
·



 . Т1
. Т1
. 1
.
.
.
.
. 5
.
. 6 4
.
.
.
.
. 7
. 3
.
.
.
8 2
.
.
. 1
.
.
.
.
.
Для определения точки пересечения каждую из образующих заключим во вспомогательную плоскость, таким образом чтобы фигурой сечения плоскости и конуса была окружность.
Точка пересечения окружности с образующей будет принадлежать одновременно трем поверхностям - вспомогательной плоскости, конусу и геликойду. Построим обе проекции этой точки. Они лежат на образующей геликойда.
Построение образующих геликойда начнем с горизонтальной проекции. Для этого окружность разобьем на восемь частей.
Вспомним как мы это уже делали. Найдем фронтальную проекцию образующей воспользовавшись винтовой линией - гелисой.
Заключим образующую во фронтальнопроецирующую плоскость Т, которая рассечет конус параллельно основанию. Радиус окружности можно замерить от оси до очерковой образующей конуса.
Построим эту окружность на горизонтальной проекции. Она пересечет образующую геликойда в некоторой точке которая будет принадлежать искомой фигуре сечения. Найдем фронтальную проекцию этой точки.
Далее аналогично.
Пересечение двух поверхностей способом сфер или вспомогательных шаровых поверхностей.
Если пересекаются две поверхности вращения общего вида с пересекающимися осями и общей плоскостью симметрии. Запишем такую теорему: Если центр секущей сферы находится на оси поверхности вращения ,ТОЧКУ ПЕРЕСЕЧЕНИЯ ОСЕЙ ПОВЕРХНОСТЕЙ ПРИНИМАЕМ ЗА ЦЕНТР ВСПОМОГАТЕЛЬНЫХ СФЕР.
12Î22ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ.
Через заданную прямую проводят вспомогательную поверхность. Находят линию пересечения вспомогательной поверхности с заданной… Определяют общие точки прямой с линией пересечения поверхностей. Это и будут искомые точки.11 21
Рассмотрим аналогичную задачу, но более сложный случай, когда плоскость частного положения в качестве дополнительной секущей провести нельзя.






 S 2
S 2
l 2
1. 2 2 2


 T2
T2
 К2
К2




 P 2
P 2
3 2 4 2
 |
S 1
 |




 l 1
l 1
 11 21
11 21
Т 1
К 1
Р 1
3 1 4 1
Проведем линию через вершину конуса и пересекающую заданную прямую. Эти две линии зададут нам плоскость общего положения пересекающую поверхность конуса.
Построение начнем с фронтальной проекции. Проведем проекцию S2 T2 и продлим ее до пересечения с проекцией прямой проходящей через основание конуса в точке Р2.
Продлим также проекцию прямой l 2 до пересечения с проекцией прямой проходящей через основание конуса в точке К 2.
Переходим к построениям на горизонтальной плоскости проекций.
По линии проекционной связи на проекции прямой l 1
найдем Т 1.
На продолжении S1 T1 на линии проекционной связи найдем положение Р 1.
Так как точка К принадлежит прямой L , то найдем ее проекцию К 1 по линии проекционной связи на продолжении
l 1.
Теперь у нас есть две точки Р 1 и К 1 для того, чтобы
провести линию проходящую через основание конуса и одновременно принадлежащую плоскости в которую мы заключили прямую L.
Проведем горизонтальную проекцию этой прямой, которая пересечет основание конуса в точках 31 и 41.
Соединив проекции этих точек с вершиной S 1 получим проекцию фигуры сечения .
Там где прямая l 1 пересечет фигуру сечения будут точки 11 и 21. Это горизонтальные проекции точек пересечения прямой L с поверхностью конуса.
Найдем фронтальные проекции этих точек. Для этого определим положение точек 32 и 42 и соединим их с вершиной S2. Остальное очевидно.
Пересечение прямой и поверхности.
Для контроля усвоения материала хочу предложить выполнить самостоятельно две…– Конец работы –
Используемые теги: Введение, курс, курс, лекций, Начертательная, Геометрия0.089
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Введение в курс. Курс лекций Начертательная геометрия
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов