ПОВНИЙ ДИФЕРЕНЦІАЛ ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ
Нехай функція z=f(х;y) має неперервні частинні похідні 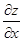 і
і  у даній області, тоді її повний приріст ∆z у точці M(x;y) можна подати у вигляді:
у даній області, тоді її повний приріст ∆z у точці M(x;y) можна подати у вигляді:
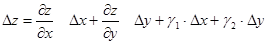 , (3.11)
, (3.11)
де  і
і  при
при 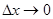 і
і  .
.
Означення 14. Функція z=f(х;y) називається диференційованою у точці M(x;y), якщо її повний приріст ∆z у даній точці можна подати у вигляді суми двох додатків: величини 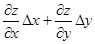 , лінійної відносно ∆х і ∆y та величини
, лінійної відносно ∆х і ∆y та величини 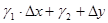 , нескінченно малої вищого порядку відносно
, нескінченно малої вищого порядку відносно  . Головна лінійна частина приросту називається повним диференціалом цієї функції і позначається dz або df (x;y):
. Головна лінійна частина приросту називається повним диференціалом цієї функції і позначається dz або df (x;y):
 . (3.12)
. (3.12)
Означення 15. Прирости незалежний змінних ∆х і ∆y називаються диференціалами незалежних змінних х і y та позначаються dх і dy відповідно.
Тоді повний диференціал (3.12) функції двох змінних має вигляд:
 . (3.13)
. (3.13)
Рівність (3.11), використовуючи (3.12), можна подати у вигляді:
 . (3.14)
. (3.14)
З точністю до нескінченно малої вищого порядку відносно 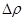 можна записати наближену рівність:
можна записати наближену рівність:
∆z≈dz. (3.15)
Наближену формулу (3.15) запишемо у точці M0(x0;y0):
 або
або
 (3.16)
(3.16)
Формулу (3.16) широко використовують у наближених обчисленнях.
Приклад 6. Знайти повний диференціал функції 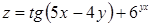 .
.
Спочатку знайдемо частинні похідні:
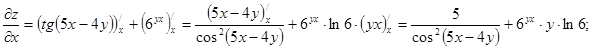
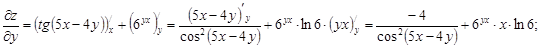
Використовуючи формулу (3.13), маємо

Приклад 7. Обчислити наближено 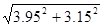 .
.
Розглянемо допоміжну функцію  . Щоб скористатись формулою (3.16), покладемо
. Щоб скористатись формулою (3.16), покладемо 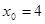 ,
,  . Тоді:
. Тоді:

Знайдемо частинні похідні:
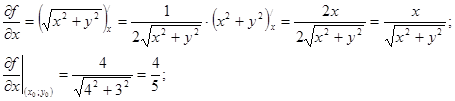

За формулою (3.16) маємо:

Отже,  .
.