Параметрические и канонические уравнения прямой
Положение прямой l однозначно определяется точкой M0 на прямой и вектором 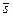 ,коллинеарным ей. Вектор
,коллинеарным ей. Вектор 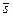 называется направляющим вектором прямой.
называется направляющим вектором прямой.
Пусть 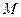 -текущая точка на прямой l, т.е. точка, пробегающая всю прямую, и пусть Oxyz - прямоугольная декартова система.
-текущая точка на прямой l, т.е. точка, пробегающая всю прямую, и пусть Oxyz - прямоугольная декартова система.
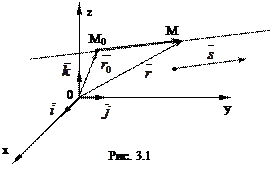
Векторы  и
и 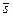 коллинеарны (рис. 3.1.).
коллинеарны (рис. 3.1.).
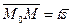 ,где
,где  -число
-число
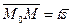 ,
, 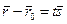 или
или 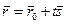 (3.1.1)
(3.1.1)
Уравнение (3.1.1.) носит название векторного параметрического уравнения прямой. Очевидно, что уравнение (3.1.1.) справедливо для векторного пространства любой размерности. Скалярные уравнения прямой в пространстве получим с помощью координат векторов и точек. Обозначим координаты точек 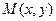 и
и 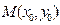 , если изучается прямая на плоскости, и через
, если изучается прямая на плоскости, и через 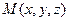 и
и  , если прямая в пространстве, соответственно координаты направляющего вектора обозначим
, если прямая в пространстве, соответственно координаты направляющего вектора обозначим 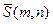 и
и  . Тогда получим параметрические уравнения прямой:
. Тогда получим параметрические уравнения прямой:
· для плоскости
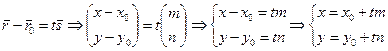 (3.1.2)
(3.1.2)
· для пространства
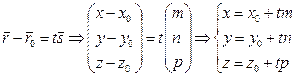 (3.1.3)
(3.1.3)
Решая уравнение (3.1.2) относительно  ,получимканонические уравнения:
,получимканонические уравнения:
· для плоскости
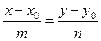 (3.1.4)
(3.1.4)
· для пространства
 (3.1.5)
(3.1.5)
Аналогично могут быть получены уравнения прямой в пространстве любой размерности.
Перепишем уравнения (3.1.2) в виде (получается исключением  из (3.1.2))
из (3.1.2))
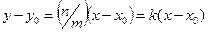 (3.1.6)
(3.1.6)
где 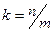 называется угловым коэффициентом прямой на плоскости,
называется угловым коэффициентом прямой на плоскости, 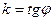 , где
, где 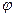 , называемый углом наклона прямой l к оси Ox, равен углу, который прямая образует с положительным направлением оси Ox. Этот угол считается положительным, если он отсчитывается от оси Oxпротив часовой стрелки, и отрицательным - по часовой стрелке (3.1.2).
, называемый углом наклона прямой l к оси Ox, равен углу, который прямая образует с положительным направлением оси Ox. Этот угол считается положительным, если он отсчитывается от оси Oxпротив часовой стрелки, и отрицательным - по часовой стрелке (3.1.2).
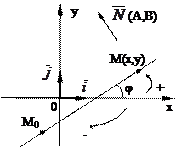 |
Рис. 3.2.
Преобразуя уравнение (3.1.6), получим уравнение прямой с угловым коэффициентом
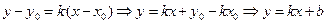 , где
, где  (3.1.7)
(3.1.7)
Уравнение прямой, проходящей через две заданные точки 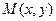 и
и 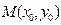 , получим из уравнения (3.1.2) заменой
, получим из уравнения (3.1.2) заменой 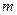 на
на 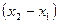 и
и  на
на 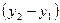 (за направляющий вектор можно взять вектор
(за направляющий вектор можно взять вектор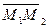 )
)
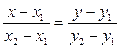 (3.1.8)
(3.1.8)