Поворот осей координат
Рис.4.2
Из рис.4.2 видно, что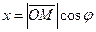 
, 
, 
, 
.
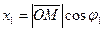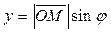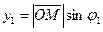Учитывая, что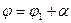 
, из этих формул получим:
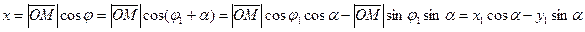
Окончательно, получим:
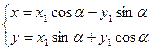(4.2.1)
или 
(4.2.2)
Замечание 1. Формулы (4.2.2) можно получить из соотношений (4.2.1), рассматривая их как уравнения, определяющие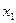 
и 
через 
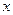и 
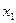, и разрешая их относительно и .
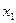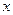Замечание 2. Формулы (4.2.2) называют формулами обратного перехода, которые выражают координаты и через и .
Рассмотрим матрицу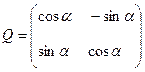 
и векторы
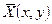и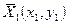 
.
Матрица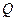 
невырожденная, т.к. определитель этой матрицы отличен от нуля
.
Тогда формулы (4.2.1) в матричном виде имеют вид 
, т.е.
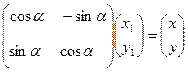, (4.2.3)
а формулы (4.2.2) имеют вид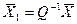 
, т.е.
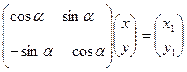(4.2.4)
можно проверить, что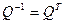 
.
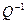- обратная матрица матрицы .
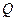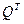- транспонированная матрица матрицы .
.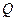
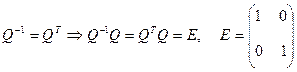