Координатное представление векторов
Пусть мы имеем прямоугольную систему координат в пространстве. Обозначим единичные векторы (орты ) осей Ox, Oy, Oz соответственно через  причем
причем  .
.
Разложим произвольный вектор 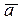 трехмерного пространства по ортам. Для этого построим вектор
трехмерного пространства по ортам. Для этого построим вектор 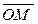 , равный вектору
, равный вектору 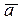 . Из точки Мопустим перпендикуляр на плоскостьхOу. Из основания этого перпендикуляра (точка А) опустим перпендикуляры на оси координат Ох и Оу и соединим точку А с началом О. На векторах
. Из точки Мопустим перпендикуляр на плоскостьхOу. Из основания этого перпендикуляра (точка А) опустим перпендикуляры на оси координат Ох и Оу и соединим точку А с началом О. На векторах 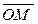 и
и  построим прямоугольник ОАММ3, диагональю которого будет вектор
построим прямоугольник ОАММ3, диагональю которого будет вектор 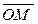 . Из рис. 1.7 видно, что
. Из рис. 1.7 видно, что 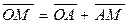 или
или 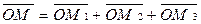 .
.

Рис. 1.7
Векторы 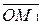 ,
, 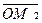 ,
,  называются составляющими или компонентами вектора
называются составляющими или компонентами вектора 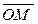 , а их величины |
, а их величины |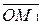 |=Х, |
|=Х, |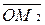 |=Y, |
|=Y, |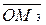 |=Z координатами этого вектора.
|=Z координатами этого вектора.
Определение 1.Проекции вектора на соответствующие координатные оси называется его составляющими или компонентами.
Определение 2.Величины проекций вектора на соответствующие координатные оси называются его координатами.
Компоненты вектора 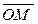 выразим через его координаты и единичные векторы
выразим через его координаты и единичные векторы  :
: 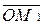 =Хi,
=Хi, 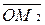 =Yj,
=Yj, 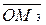 =Zk .
=Zk .
Подставляя эти значения в равенство 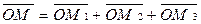 и обозначив
и обозначив 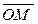 через
через 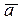 получим:
получим:
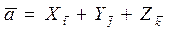 (1.4.1)
(1.4.1)
Равенство (1.4.1) можно записать в виде:
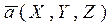 (1.4.2)
(1.4.2)
Замечание 1.Равные векторы имеют одинаковые координаты.
Замечание 2.Разложение вектора 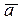 в виде (1.4.1) возможно только единственным способом.
в виде (1.4.1) возможно только единственным способом.
Из единственности разложения (1.4.1) вектора 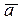 по ортам, следует, что если координаты любых двух векторов
по ортам, следует, что если координаты любых двух векторов 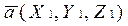 и
и  равны, т.е.
равны, т.е. 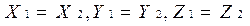 , то эти векторы тоже равны .
, то эти векторы тоже равны .
Вектор 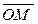 , идущий от начала точки О к точке
, идущий от начала точки О к точке 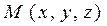 называется радиус - вектором этой точки, и его координаты совпадают с соответствующими координатами точки
называется радиус - вектором этой точки, и его координаты совпадают с соответствующими координатами точки 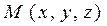 (рис. 1.8), Х=х, Y=y, Z=z.
(рис. 1.8), Х=х, Y=y, Z=z.
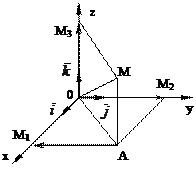 |
Рис. 1.8
Поэтому 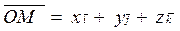 , или
, или 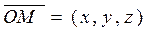 . Пусть
. Пусть  - вектор, координаты начала и конца которого известны
- вектор, координаты начала и конца которого известны  и
и 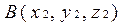 . Тогда координаты вектора
. Тогда координаты вектора 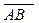 выражаются по формулам :
выражаются по формулам :
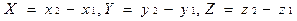 (1.4.3)
(1.4.3)
Из рис. 1.9 видно, что
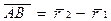 (1.4.4)
(1.4.4)
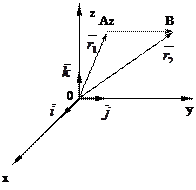
Рис. 1.9
Используя свойства проекций (п.1.2.), имеем:  , и аналогичным образом находим
, и аналогичным образом находим  .
.
Разложение вектора 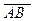 по ортам будет иметь следующий вид:
по ортам будет иметь следующий вид:
 (1.4.5)
(1.4.5)
Тройка векторов 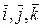 называется координатным базисом, а разложение (1.4.1) вектора
называется координатным базисом, а разложение (1.4.1) вектора 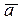 называется разложением вектора
называется разложением вектора 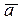 по базису
по базису 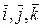 .
.
Замечание.Разложение вектора 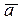 на плоскости по базису
на плоскости по базису 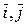 имеет вид
имеет вид 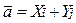 .
.
1.5. Операции над векторами, заданными
в координатной форме
Если векторы заданы в координатной форме, то операции сложения и вычитания векторов, умножения вектора на число можно заменить более простыми арифметическими операциями над координатами этих векторов по следующим правилам.
Правило 1.При сложении векторов их одноименные координаты складываются:
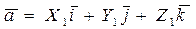 ,
,  ,
,
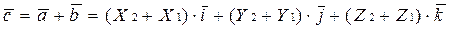 (1.5.1)
(1.5.1)
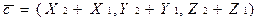
Правило 2.Чтобы вычесть из вектора 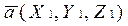 вектор
вектор  , нужно вычест координаты вектора
, нужно вычест координаты вектора 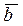 из соответствующих координат вектора
из соответствующих координат вектора 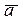 , т.е.
, т.е.
 или
или 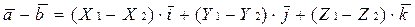 (1.5.2)
(1.5.2)
Правило 3. Чтобы умножить вектор 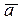 на число
на число 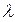 , нужно умножить на это число его координаты , т.е. если
, нужно умножить на это число его координаты , т.е. если 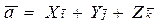 , то
, то 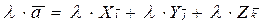 .
.