Скалярное произведение векторов, заданных координатами
Так как единичные векторы (орты) 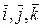 осей Ox, Oy, Ozпрямоугольной системы координат взаимноперпендикулярны, то по формуле (1.6.1) получим :
осей Ox, Oy, Ozпрямоугольной системы координат взаимноперпендикулярны, то по формуле (1.6.1) получим :
 ,
, 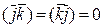 ,
, 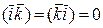 (1.6.2.1)
(1.6.2.1)
Далее, используя свойство скалярного произведения  имеем:
имеем:
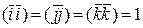 (1.6.2.2)
(1.6.2.2)
Пусть, 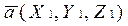 ,
,  . Найдем произведение этих векторов (с учетом формул 1.6.2.1 и 1.6.2.2 ):
. Найдем произведение этих векторов (с учетом формул 1.6.2.1 и 1.6.2.2 ):
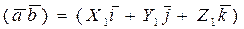
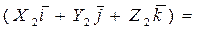
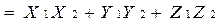 (1.6.2.3)
(1.6.2.3)
Таким образом, скалярное произведение двух векторов равно сумме произведений одноименных координат этих векторов.
Из равенства (1.6.2.3) и равенства векторов получим:
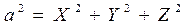 (1.6.2.4)
(1.6.2.4)
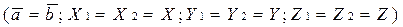 ,
,
т.е. квадрат длины вектора равен сумме его координат .
Из равенства (1.6.2.4) найдем длину вектора 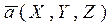 :
:
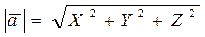 (1.6.2.5)
(1.6.2.5)
Длина вектора равна квадратному корню из суммы квадратов его координат.