Линейная регрессия

Регрессионный анализ - раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным. Проблема регрессии в математической статистике характерна тем, что распределениях изучаемых величин нет достаточной информации.

Цель РА состоит в определении общего вида уравнения регрессии, построении оценок неизвестных параметров, входящих в уравнение регрессии и проверке статистических гипотез о регрессии. При изучении связи между двумя величинами по результатам наблюдений (х₁, у₁),…, (х_n,y_n) в соответствии с теорией регрессии предполагается, что одна из них У имеет некоторое распределение вероятностей при фиксированном значении х другой, так что

Е(У|х) =g(х,b) и D(У|х)=s²h²(x),

где b обозначает совокупность неизвестных параметров, определяющих функцию g(х), а h(х) есть известная функция х (в частности, тождественно равная 1) и нужно по результатам наблюдений определить значения параметров. Выбор модели регрессии определяется предположениями о форме зависимости g(x,b) от х и b. Наиболее естественной с точки зрения единого метода оценки неизвестных параметров b является модель регрессии, линейная относительно b:

g(x,b)=b₀g₀(x)+…+b_kg_k(x).

Относительно значений переменной х возможны различные предположения в зависимости от характера наблюдений и целей анализа. Для установления связи между величинами в эксперименте используется модель, основанная на упрощённых, но правдоподобных допущениях: величина х является контролируемой величиной, значения которой заранее задаются при

 

планировании эксперимента, а наблюдаемые значения у представимы в виде

У_i =g(x_i,b)+е_i, i = 1,…,k,

где величины е_i характеризуют ошибки, независимые при различных измерениях и одинаково распределенные с нулевым средним и постоянной дисперсией s².

Случай неконтролируемой переменной х отличается тем, что результаты наблюдений (х_i, у_i),…,(x_n, у_n) представляют собой выборку из некоторой двумерной совокупности. И в том, и в другом случае РA производится одним и тем же способом, однако интерпретация результатов существенно различается (если обе исследуемые величины случайны, то связь между ними изучается методами корреляционного анализа).

Предварительное представление о форме графика зависимости g(х) от х можно получить по расположению на диаграмме рассеяния (называемой также корреляционным полем, если обе переменные случайные) точек (х_i,y(x_i)), где у(x_i) - средние арифметические тех значений у, которые соответствуют фиксированному значению х_i. Например, если расположение этих точек близко к прямолинейному, то допустимо использовать в качестве приближения линейную регрессию. Стандартный метод оценки линии регрессии основан на использовании полиномиальной модели

у(х,b)=b₀+b₁x+…+b_mx^m

(этот выбор отчасти объясняется тем, что всякую непрерывную на некотором отрезке функцию можно приблизить полиномом с любой на заданной степенью точности). Оценка неизвестных коэффициентов регрессии b₀…b_m и неизвестной дисперсии s² осуществляется методом наименьших квадратов.

Оценки 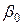,…,параметров b₀…b_m , полученные этим методом, называются выборочными коэффициентами регрессии, а уравнение

определяет т.н. эмпирическую линию регрессии. Этот метод в предположении нормальной распределенности результатов наблюдений приводит к оценкам для b₀…b_m и s² ,совпадающим с оценками наибольшего правдоподобия. Оценки, полученные этим методом, оказываются в некотором смысле наилучшими и в случае отклонения от нормальности. Так, если проверяется гипотеза о линейной регрессии, то

, , , ,

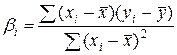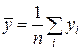где x и у - средние арифметические значений х_i и у_i, и оценка g(x)=- будет несмещенной для g(x), а её дисперсия будет меньше, чем дисперсия любой другой линейной оценки:

.

Случайные величины 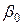,…,называются выборочными коэффициентами регрессии. Многочлен , построенный методами наименьших квадратов, называется эмпирической линией регрессии.

Если дисперсия зависит от x, то метод наименьших квадратов применим с некоторыми видоизменениями.

Если изучается зависимость случайной величины y от нескольких переменных x₁,…,x_k, то общую линейную модель регрессии удобнее записывать в матричной форме: вектор наблюдений y с независимыми компонентами y₁,…,y_n имеет среднее значение и ковариационную матрицу

E(y| x₁,…,x_k)=xb, D(y| x₁,…,x_k)=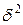I (*), где b=(b₁,…,b_k) – вектор коэффициентов регрессии, X=||x_ij||, i=1,…,n, j=1…k,- матрица известных величин, связанных друг с другом, вообще говоря, произвольным образом, I – единичная матрица n-го порядка; при этом n>k и |X^TX|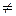0. В более общем случае допускается корреляция между наблюдениями y_i:

E(y| x₁,…,x_k)=xb, D(y| x₁,…,x_k)=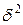А, где матрица А известна, но эта схема сводится к модели (*). Несмещенной оценкой b по методу наименьших квадратов является величина , а смещенной оценкой для 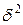служит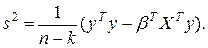

Модель (*) является наиболее общей линейной моделью, поскольку она применима к различным регрессионным ситуациям и включает в себя все виды параболической регрессииy по x₁,…,x_k. При таком линейном понимании РА задача оценки b и вычисления ковариационной матрицы оценок Db=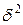(X^TX)^-1 cводится к задаче обращения матрицы X^TX.

Указанный метод построения эмпирической регрессии в предположении нормального распределения результатов наблюдений приводит к оценкам для b и 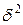, совпадающим с оценками наибольшего правдоподобия. Однако оценки, полученные этим методом, являются в некотором смысле наилучшими и в случае отклонения от нормальности, если только объем выборки достаточно велик.

Задачи РА не ограничиваются построением точечных оценок параметров b и 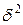общей линейной модели (*). Проблема точности построенной эмпирической зависимости наиболее эффективно разрешается при допущении, что вектор наблюдений y распределен нормально.

При допущении, что величины y_iнормально распределены, наиболее эффективно осуществляется проверка точности построенной эмпирической регрессионной зависимости и проверка гипотез о параметрах регрессионной модели. В этом случае построение доверительных интервалов для истинных коэффициентов регрессии b₀…b_m и проверка гипотезы об отсутствии регрессионной связи b_i,=0, i = 1,…,m производится с помощью распределения Стьюдента.

В более общей ситуации результаты наблюдений у_1…y_n рассматриваются как независимые случайные величины с одинаковыми дисперсиями и математическими ожиданиями

Еу_i = b₁x₁+…+b_ix_ki, i = 1,...,n,

где значения х_jj, j‚ = 1,...,k предполагаются известными. Эта форма линейной модели регрессии является общей в том смысле, что к ней сводятся модели более высоких порядков по переменным x_1…x_k,. Кроме того, некоторые нелинейные относительно параметров b_i модели подходящим преобразованием также сводятся к указанной линейной форме.

РA является одним из наиболее распространённых методов обработки результатов наблюдений при изучении зависимостей в физике, биологии, экономике, технике и др. областях. На моделях РA. основаны такие разделы математической статистики, как дисперсионный анализ и планирование эксперимента; модели РА широко используются в многомерном статистическом анализе.