Критерий Смирнова

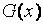Предполагается, что функции распределения и явля­ются непрерывными. Статистика критерия Смирнова измеряет различие ме­жду эмпирическими функциями распределения, построенными по выборкам

.

При практическом использовании критерия значение статистики рекомен­дуется вычислять в соответствии с соотношениями

,

,

.

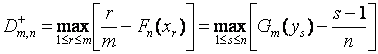Если гипотеза H₀ справедлива, то при неограниченном увеличении объемов выборок ,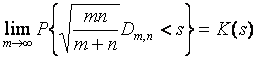

т.е. статистика в пределе подчиняется распределению Колмогорова 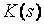- предельное распределение, к которому стремится при n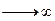распределение статистики

,

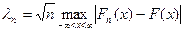где функция выборочного распределения F_n(x)-несмещенная точечная статистическая оценка для непрерывной ф-и теоретического распределения F(x). Т.е. статистика

(1)

в пределе подчиняется распределению Колмогорова.

Однако иногда при огр. значениях m,n случайные величины D_m,n и D_m,n ⁺ являются дискретными, и множество их возможных значений представляет собой ре­шетку с шагом , где k наименьшее общее кратное n и m. Для значе­ний 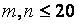таблицы процентных точек для статистики D_m,n приводятся в [3]. Условное распределение статистики S_c при справедливости ги­потезы H₀ медленно сходится к 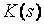и существенно отличается от него при не очень больших m и n. Асимптотические формулы для распределений D_m,n и D_m,n ⁺ рассматривались в [7, 8, 9].

На рис. 1 показаны условные распределения статистики (1) при спра­ведливости H₀ в зависимости от m и n (при m=n). Как следует из получен­ной кар­тины, даже пр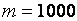и и ступенчатость со­храня­ется. Другим недостатком применения критерия со статистикой (1) является то (см. рис. 1), что рас­пределения с ростом m и n приближаются к предельному распреде­лению 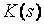слева.

Рис. 1. Распределения статистики (1) при справедливости H₀ в зависимости от m,n

Гладкость распределения статистики сильно зависит от величины k. По­этому предпо­чти­тельнее применять критерий, когда объемы выборок m,n не равны и представляют собой вза­имно простые числа. В таких случаях наименьшее общее кратное m,n максимально и равно k=mn, а распределе­ние статистики существенно больше напоминает непрерывную функцию распределения. 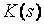И вот тогда при небольших и умеренных значениях m,n проявляется существенное отличие распределения от предель­ного , так как заметно сдвинуто влево от .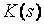

В этой связи можно предложить следующую простую модификацию статистики (1),

, (2)

у которой практически отсутствует последний недостаток. Условные распре­деления статистики (2) при справедливости H₀ в зависимости от m,n (при m=n) иллюстрирует рис. 2.

 

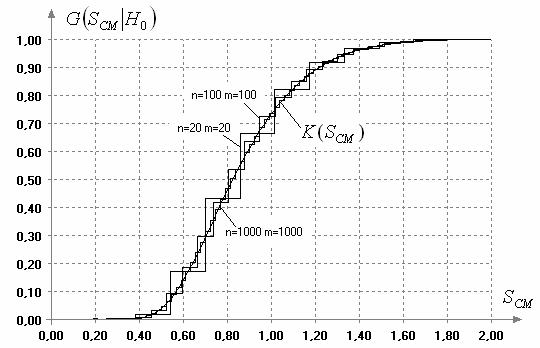
Рис. 2. Распределения статистики (2) при справедливости H₀ в зависимости от m,n

Как было сказано выше, гладкость распределения статистики зависит от величины k. В качестве иллюстрации этого факта и различий в распределе­ниях статистик (1) и (2) на рис. 3 приведены предельное распреде­ление Колмогорова 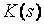и полученные в результате моделирования эмпириче­ские распределения статистики (1) и стати­стики (2) при и . Как видим, распределение статистики (1) суще­ственно отличается от распределения Колмогорова 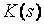, а распределе­ние статистики (2) визуально практически совпадает с ним. Объем выборок смоделированных значений статистик в данном случае, как и во всех осталь­ных в данной работе, составил 10000 наблюдений. При проверке согласия полученного эмпирического рас­пределения статистики (2) с распределением Колмогорова достигнутые уровни значимости по соответствующим крите­риям составили: 0.72 по критерию 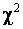Пирсона (при 10 равновероятных интер­валах), 0.83 по критерию Колмогорова, 0.97 по критерию 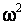Крамера-Мизеса-Смирнова, 0.94 по критерию 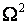Андерсона-Дарлинга.

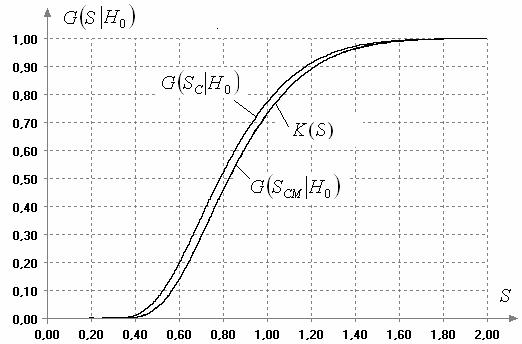
Рис. 3. Распределения статистики (1) и (2) при справедливости H₀, m=61, n=53

Использование в критерии Смирнова со статистикой (2) взаимно про­стых m,n делает более обоснованным вычисление достигаемого уровня зна­чимости , где S_CM^* – значение ста­тистики (2), найденное при проверке гипотезы H₀ по конкретным выборкам, в соответ­ствии с распределением Колмогорова: . Со­ответственно, более правомерно применение в критерии процентных то­чек (квантилей) распределения Колмогорова. Этого нельзя сказать относи­тельно критерия Смирнова со статистикой (1), так как в этом случае критиче­ские значения, определяемые по распределению Колмогорова, оказываются завышенными по сравнению с истинными. Следовательно, проверяемая ги­потеза может необоснованно приниматься (не отклоняться).

Коэффициент 4.6 в статистике (2) подобран эмпирически. Он удовле­творительно действует от малых до очень приличных объемов выборок (m=n=1000). Однако при больших значениях наименьшего общего кратного m,n, когда они представляют собой взаимно простые числа, величина этого коэффициента должна быть несколько уменьшена. Например, при про­стых и 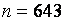коэффициент 4.6 следует заменить на 3.4.

Ниже при исследовании мощности критерия Смирнова рас­смат­ри­ва­лись распределения статистики (1). Но все выводы относительно мощности справедливы и для кри­те­рия со статистикой (2), так как все распределения при одинаковых объемах выборок оказываются сдвинутыми на одну и ту же величину [см. (2)].

Предвосхищая вопросы о точности, отметим, что для проверки соответствия результатов моделирования имеющимся теоретическим [3] нами специально моделировались распределения статистики D_m,n. Результаты показали полное совпадение критических значений, получаемых в процессе моделирования, с точными критическими значениями статистики, приводимыми в [3].

В данной работе мощность критериев проверки однородности исследо­валась при ряде альтернатив. Для определенности гипотезе H₀ соответство­вала принадлежность выборок одному и тому же стандартному нормальному закону распределения с плотностью

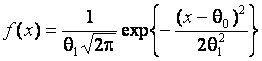
с параметрами сдвига и масштаба . При всех альтернативах пер­вая выборка всегда соответствовала стандартному нормальному закону, а вторая – некоторому другому. В частности, в случае гипотезы H1 вторая вы­борка соответствовала нормальному закону с параметром сдвига 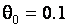и па­раметром масштаба . В случае гипотезы H2 – нормальному закону с параметрами и . В случае гипотезы H3 – нормальному закону с параметрами и 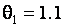. В случае гипотезы H4 – нормальному за­кону с параметрами и 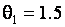. В случае гипотезы H5 – вторая вы­борка соответствовала логистическому закону с плотностью

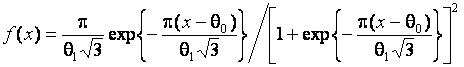
и параметрами и . Нормальный и логистический законы очень близки и трудно разли­чимы с помощью критериев согласия. На рис. 4 представлены полученные в результате моделирования условные распределения статистики 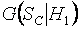при справедливости H1, на основании которых можно оценить значения мощ­ности при различных значениях объемов выборок m,n.

Рис. 4. Распределения статистики (1) при справедливости H1.

Аналогичным образом при различных объемах выборок были построены условные распределения статистики (1) при справедливости других рассматриваемых альтернатив: 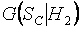, , 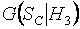, . На основании этих распределений и предельного распределения статистики = 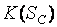были вычислены значения мощности критерия относительно различных альтернатив. Найденные значения мощности 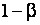критерия Смир­нова, где - вероятность ошибки второго рода, относительно рассматривае­мых конкурирующих гипотез H1 ÷ H5 при различных объемах выборок для уровней значимости (вероятностей ошибок первого рода) =0.1, 0.05, 0.025 представлены в таблице 1.

 

Таблица 1. Мощность критерия однородности Смирнова относи­тель­но альтернатив H1÷ H5 в зависимости от объемов выборок (m=n)

Уровень значимости	Значения мощности относительно альтернативы
n=20	n=50	n=100	n=300	n=500	n=1000	n=2000
0,1	0,0937	0,1480	0,1766	0,2775	0,3806	0,6171	0,8688
0,05	0,0410	0,0569	0,0944	0,1883	0,2682	0,4899	0,7762
0,025	0,0410	0,0344	0,0505	0,1163	0,1829	0,3859	0,6737
	Значения мощности относительно альтернативы
0,1	0,3457	0,7200	0,9332
0,05	0,2202	0,5341	0,8722	0,9996
0,025	0,2202	0,4328	0,7842	0,9992
	Значения мощности относительно альтернативы
0,1	0,0884	0,1229	0,1257	0,1466	0,1856	0,2967	0,5508
0,05	0,0352	0,0458	0,0630	0,0789	0,1024	0,1677	0,3520
0,025	0,0352	0,0257	0,0280	0,0410	0,0518	0,0967	0,2098
	Значения мощности относительно альтернативы
0,1	0,1396	0,2986	0,5213	0,9609	0,9989
0,05	0,0570	0,1268	0,3161	0,8977	0,9952
0,025	0,0570	0,0763	0,1689	0,7738	0,9786
	Значения мощности относительно альтернативы
0,1	0,0836	0,1209	0,1308	0,1568	0,1976	0,3191	0,5639
0,05	0,0341	0,0455	0,0673	0,0891	0,1158	0,1879	0,3754
0,025	0,0341	0,0258	0,0316	0,0471	0,0618	0,1119	0,2390

Подчеркнем, что значения мощностей, приведенные в таблице 1, получены относительно ()-квантилей предельного распределения Колмогорова 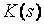. Вследствие того, что распределения статистики (1) существенно отличаются от 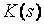, действительные уровни значимости отличаются от заданных =0.1, 0.05, 0.025. В таблице 2 приведены действительные уровни значимости для критерия Смирнова, соответствующие значениям мощности, представленным в таблице 1. Вследствие ступенчатости действи­тельные значения осо­бенно сильно отличаются от задаваемых при малых объемах выборок. Например, для при задаваемом уровне значимости 0.1 мы имеем действительный уровень значимости 0.0835.

 

 

Таблица 2. Действительные уровни значимости критерия однородности Смирнова, соответствующие (1-α)–квантилям распределения Колмогорова, в зависимо­сти от объемов выборок (n=m)

Заданный уровень значимости	Действительные уровни значимости
n=20	n=50	n=100	n=300	n=500	n=1000	n=2000
0,1	0,0835	0,1120	0,1085	0,0927	0,0970	0,0980	0,1041
0,05	0,0334	0,0410	0,0543	0,0496	0,0514	0,0471	0,0480
0,025	0,0334	0,0240	0,0252	0,0254	0,0238	0,0259	0,0245