Однофакторный дисперсионный анализ.
Однофакторная дисперсионная модель имеет вид:
xij = μ + Fj + εij, (1)
где хij – значение исследуемой переменой, полученной на i-м уровне фактора (i=1,2,...,т) c j-м порядковым номером (j=1,2,...,n);
Fi – эффект, обусловленный влиянием i-го уровня фактора;
εij – случайная компонента, или возмущение, вызванное влиянием неконтролируемых факторов, т.е. вариацией переменой внутри отдельного уровня.
Основные предпосылки ДА:
- математическое ожидание возмущения εij равно нулю для любых i, т.е.
M(εij) = 0; (2)
- возмущения εij взаимно независимы;
- дисперсия переменной xij (или возмущения εij) постоянна для
любых i, j, т.е.
D(εij) = σ2; (3)
- переменная xij (или возмущение εij) имеет нормальный закон
распределения N(0;σ2).
Влияние уровней фактора может быть как фиксированным или систематическим (модель I), так и случайным (модель II).
Пусть, например, необходимо выяснить, имеются ли существенные различия между партиями изделий по некоторому показателю качества, т.е. проверить влияние на качество одного фактора - партии изделий. Если включить в исследование все партии сырья, то влияние уровня такого фактора систематическое (модель I), а полученные выводы применимы только к тем отдельным партиям, которые привлекались при исследовании. Если же включить только отобранную случайно часть партий, то влияние фактора случайное (модель II). В многофакторных комплексах возможна смешанная модель III, в которой одни факторы имеют случайные уровни, а другие – фиксированные.
Пусть имеется m партий изделий. Из каждой партии отобрано соответственно n1, n2, …, nm изделий (для простоты полагается, что n1=n2=...=nm=n). Значения показателя качества этих изделий представлены в матрице наблюдений:

 x11 x12 … x1n
x11 x12 … x1n
x21 x22 … x2n
………………… = (xij), (i = 1,2, …, m; j = 1,2, …, n).
xm1 xm2 … xmn
Необходимо проверить существенность влияния партий изделий на их качество.
Если полагать, что элементы строк матрицы наблюдений – это численные значения случайных величин Х1,Х2,...,Хm, выражающих качество изделий и имеющих нормальный закон распределения с математическими ожиданиями соответственно a1,а2,...,аm и одинаковыми дисперсиями σ2, то данная задача сводится к проверке нулевой гипотезы Н0: a1=a2 =...= аm, осуществляемой в ДА.
Усреднение по какому-либо индексу обозначено звездочкой (или точкой) вместо индекса, тогда средний показатель качества изделий i-й партии, или групповая средняя для i-го уровня фактора, примет вид:
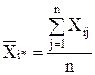 , (4)
, (4)
где 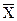 i* – среднее значение по столбцам;
i* – среднее значение по столбцам;
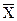 ij – элемент матрицы наблюдений;
ij – элемент матрицы наблюдений;
n – объем выборки.
А общая средняя:
 . (5)
. (5)
Сумма квадратов отклонений наблюдений хij от общей средней 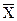 ** выглядит так:
** выглядит так:
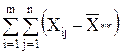 2=
2=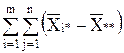 2+
2+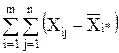 2+
2+
+2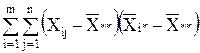 2. (6)
2. (6)
или
Q = Q1 + Q2 + Q3.
Последнее слагаемое равно нулю
 =0. (7)
=0. (7)
так как сумма отклонений значений переменной от ее средней равна нулю, т.е.
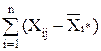 2=0.
2=0.
Первое слагаемое можно записать в виде:

В результате получается тождество:
Q = Q1 + Q2, (8)
где  - общая, или полная, сумма квадратов отклонений;
- общая, или полная, сумма квадратов отклонений;
 - сумма квадратов отклонений групповых средних от общей средней, или межгрупповая (факторная) сумма квадратов отклонений;
- сумма квадратов отклонений групповых средних от общей средней, или межгрупповая (факторная) сумма квадратов отклонений;
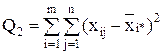 - сумма квадратов отклонений наблюдений от групповых средних, или внутригрупповая (остаточная) сумма квадратов отклонений.
- сумма квадратов отклонений наблюдений от групповых средних, или внутригрупповая (остаточная) сумма квадратов отклонений.
В разложении (8) заключена основная идея ДА. Применительно к рассматриваемой задаче равенство (8) показывает, что общая вариация показателя качества, измеренная суммой Q, складывается из двух компонент – Q1 и Q2, характеризующих изменчивость этого показателя между партиями (Q1) и изменчивость внутри партий (Q2), характеризующих одинаковую для всех партий вариацию под воздействием неучтенных факторов.
В ДА анализируются не сами суммы квадратов отклонений, а так называемые средние квадраты, являющиеся несмещенными оценками соответствующих дисперсий, которые получаются делением сумм квадратов отклонений на соответствующее число степеней свободы.
Число степеней свободы определяется как общее число наблюдений минус число связывающих их уравнений. Поэтому для среднего квадрата s12, являющегося несмещенной оценкой межгрупповой дисперсии, число степеней свободы k1=m-1, так как при его расчете используются m групповых средних, связанных между собой одним уравнением (5). А для среднего квадрата s22, являющегося несмещенной оценкой внутригрупповой дисперсии, число степеней свободы k2=mn-m, т.к. при ее расчете используются все mn наблюдений, связанных между собой m уравнениями (4).
Таким образом:
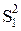 = Q1/(m-1),
= Q1/(m-1),
 = Q2/(mn-m).
= Q2/(mn-m).
Если найти математические ожидания средних квадратов 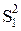 и
и  , подставить в их формулы выражение xij (1) через параметры модели, то получится:
, подставить в их формулы выражение xij (1) через параметры модели, то получится:


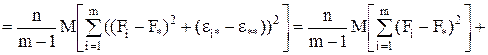

 (9)
(9)
т.к. с учетом свойств математического ожидания
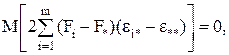 а
а
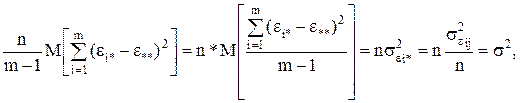
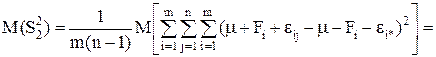
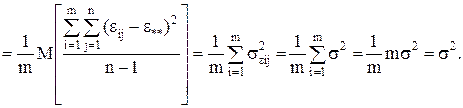 (10)
(10)
Для модели I с фиксированными уровнями фактора Fi(i=1,2,...,m) – величины неслучайные, поэтому
M(S ) =
) =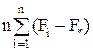 2 /(m-1) +σ2.
2 /(m-1) +σ2.
Гипотеза H0 примет вид Fi = F*(i = 1,2,...,m), т.е. влияние всех уровней фактора одно и то же. В случае справедливости этой гипотезы
M(S )= M(S
)= M(S )= σ2.
)= σ2.
Для случайной модели II слагаемое Fi в выражении (1) – величина случайная. Обозначая ее дисперсией
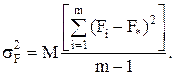
получим из (9)
 (11)
(11)
и, как и в модели I
M(S )= σ2.
)= σ2.
В таблице 1.1 представлен общий вид вычисления значений, с помощью дисперсионного анализа.
Таблица 1.1 – Базовая таблица дисперсионного анализа
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Средний квадрат | Математическое ожидание среднего квадрата |
| Межгрупповая | 
| m-1 | 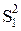 = Q1/(m-1) = Q1/(m-1)
| 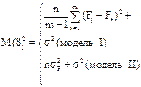
|
| Внутригрупповая | 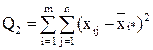
| mn-m | 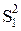 = Q2/(mn-m) = Q2/(mn-m)
| M(S )= σ2 )= σ2
|
| Общая | 
| mn-1 |
Гипотеза H0 примет вид σF2 =0. В случае справедливости этой гипотезы
M(S )= M(S
)= M(S )= σ2.
)= σ2.
В случае однофакторного комплекса как для модели I, так и модели II средние квадраты S2 и S2, являются несмещенными и независимыми оценками одной и той же дисперсии σ2.
Следовательно, проверка нулевой гипотезы H0 свелась к проверке существенности различия несмещенных выборочных оценок S и S
и S дисперсии σ2.
дисперсии σ2.
Гипотеза H0 отвергается, если фактически вычисленное значение статистики F = S /S
/S больше критического Fα:K1:K2, определенного на уровне значимости α при числе степеней свободы k1=m-1 и k2=mn-m, и принимается, если F < Fα:K1:K2 .
больше критического Fα:K1:K2, определенного на уровне значимости α при числе степеней свободы k1=m-1 и k2=mn-m, и принимается, если F < Fα:K1:K2 .
Применительно к данной задаче опровержение гипотезы H0 означает наличие существенных различий в качестве изделий различных партий на рассматриваемом уровне значимости.
Для вычисления сумм квадратов Q1, Q2, Q часто бывает удобно использовать следующие формулы:
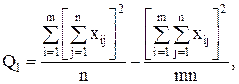 (12)
(12)
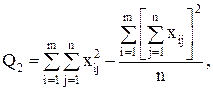 (13)
(13)
 (14)
(14)
т.е. сами средние, вообще говоря, находить не обязательно.
Таким образом, процедура однофакторного ДА состоит в проверке гипотезы H0 о том, что имеется одна группа однородных экспериментальных данных против альтернативы о том, что таких групп больше, чем одна. Под однородностью понимается одинаковость средних значений и дисперсий в любом подмножестве данных. При этом дисперсии могут быть как известны, так и неизвестны заранее. Если имеются основания полагать, что известная или неизвестная дисперсия измерений одинакова по всей совокупности данных, то задача однофакторного дисперсионного анализа сводится к исследованию значимости различия средних в группах данных.