Замечание о представлении произвольной формулы многочленом Жегалкина.

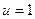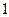Введём следующие обозначения: , . Тогда конъюнкция станет обычным умножением символов и . Действительно:

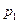
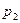
Договоримся далее в наших рассуждениях обозначать конъюнкцию точкой и опускать её в записи формул (как принято в алгебре). Например, 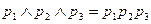. Такие произведения будем называть одночленами Жегалкина. Одночлены, объединённые знаком «+», называются многочленами Жегалкина.

Известно, что система операций 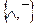полна, причём , поэтому всякую формулу алгебры логики можно преобразовать с помощью операций 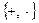. Это значит, что любую формулу алгебры логики можно представить многочленом Жегалкина, причём единственным образом. Чтобы получить такое представление нужно выразить все логические операции, входящие в формулу, через конъюнкцию и отрицание, учитывая, что , 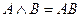. Далее нужно раскрыть скобки, привести подобные слагаемые, имея в виду, что для любых одночленов выполняются свойства: , , , .

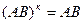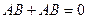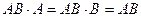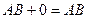Представим основные логические операции многочленами Жегалкина.

1) - есть многочлен Жегалкина (одночлен второй степени);

2)

(здесь учитывается, что 1 + 1 = 0);

3) .

Эквивалентность рассматривается аналогично.

Рассмотрим для примера следующую формулу: . Получим представление этой формулы в виде многочлена Жегалкина:

= = = = = .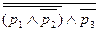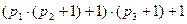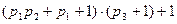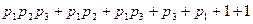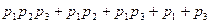