рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- КУРС ЛЕКЦИЙ ПО МАТЕМАТИЧЕСКОЙ ЛОГИКЕ
Реферат Курсовая Конспект
КУРС ЛЕКЦИЙ ПО МАТЕМАТИЧЕСКОЙ ЛОГИКЕ
КУРС ЛЕКЦИЙ ПО МАТЕМАТИЧЕСКОЙ ЛОГИКЕ - раздел Математика, Министерство Образования И Науки Украины Восточноукр...
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
имени ВЛАДИМИРА ДАЛЯ
КУРС ЛЕКЦИЙ
ПО МАТЕМАТИЧЕСКОЙ ЛОГИКЕ
У т в е р ж д е н оВведение.
Логика занимается анализом методов рассуждений; при этом основное внимание направлено на форму, а не на содержание конкретных доводов. Разговорные языки на протяжении длительного времени развивались как средство общения, а это не всегда совместимо с точностью и надежностью логического анализа. При этом текстуальное сходство не может быть свидетельством тождественности логической формы. Для иллюстрации приведем следующий пример:
1. Я видел портрет Ползунова. Ползунов – изобретатель паровой машины, следовательно, я видел портрет изобретателя паровой машины.
2. Я видел портрет кого-то; кто-то изобрел колесо; следовательно, я видел портрет изобретателя колеса.
Внешнее языковое сходство этих рассуждений обманчиво, что обнаруживается, если обратиться к содержанию. Но существуют более тонкие примеры, где ошибку обнаружить сложнее.
Кроме того, богатство языка, наличие синонимов, имеющих разные смысловые оттенки в разных контекстах, не позволяют использовать разговорный язык в строгом логическом анализе. Возьмем, например, фразы «великий русский поэт А. С. Пушкин» и «автор «Евгения Онегина»», определяют ли эти фразы одно и то же? Если это синонимы, то в любом предложении можно заменить одну из этих фраз другой, не меняя смысла предложения.
Возьмем предложение: «Великий русский поэт А.С. Пушкин является автором «Евгения Онегина»» и заменим в этом предложении одну из двух фраз другой, получим предложение: «Великий русский поэт А.С. Пушкин является А.С. Пушкиным». Таким образом, из предложения, имеющего смысл, мы получим предложение, лишенное смысла.
Математическая логика возникла в середине XIX века, но получила мощный толчок для развития в конце XIX века открытием парадоксов теории множеств. Напомним некоторые из парадоксов.
1. Парадокс Рассела (1902): Как правило, множества не содержат самих себя в качестве своего элемента. Например, множество простых чисел не является простым числом. Но так как никаких ограничений на множества не накладывается, то можно представить себе и множества, которые содержат себя в качестве своих элементов. Назовем такие множества неправильными. Таким образом, множество является правильным, если оно не содержит себя в качестве своего элемента.
Пусть  – множество всех правильных множеств. Теперь поставим вопрос: будет ли множество
– множество всех правильных множеств. Теперь поставим вопрос: будет ли множество  правильным или неправильным? Предположим, что
правильным или неправильным? Предположим, что  – правильное, но все правильные множества являются элементами множества
– правильное, но все правильные множества являются элементами множества  , т. е. тогда
, т. е. тогда  содержит себя в качестве одного из элементов, значит множество
содержит себя в качестве одного из элементов, значит множество  – неправильное. Предположим, что это так, тогда
– неправильное. Предположим, что это так, тогда  является элементом
является элементом  , но множество
, но множество  , по определению, содержит лишь правильные множества, и значит,
, по определению, содержит лишь правильные множества, и значит,  должно быть правильным. Получено логическое противоречие.
должно быть правильным. Получено логическое противоречие.
2. Парадокс Кантора (1899): С одной стороны множество всех множеств должно иметь наибольшую мощность, с другой стороны, мощность множества всех его подмножеств должна быть ещё большей.
3. Парадокс Бурелли-Форти (1897): Этот парадокс аналогичен парадоксу Кантора, но возникает в теории порядковых (ординальных чисел). Для любого ординального числа существует ординальное число, следующее за ним. Однако ординальное число, определяемое множеством всех ординальных чисел, является наибольшим порядковым числом.
Кроме парадоксов теории множеств существует ещё семантические парадоксы. Рассмотрим наиболее известные из них.
4. Парадокс лжеца: Некто говорит «Я лгу». Если он при этом лжёт, то сказанное им ложь, т.е. он сказал правду. Если же он не лжёт, то сказанное им есть истина, и, следовательно, он лжёт. Т.е. он и лжёт и не лжёт одновременно. С парадоксом лжеца имеет сходство известный ещё в древности «парадокс критянина». Критский философ Эпименид сказал: «Все критяне – лжецы». Если он сказал правду, то, поскольку сам Эпименид критянин, сказанное им есть ложь. Если сказанное им ложь, то существуют критянин, который не лжёт.
5. Парадокс Берри (1906): Существует конечное число слогов в русском языке. Следовательно, имеется лишь конечное число таких фраз русского языка, которые содержат не более пятидесяти слогов. Поэтому с помощью таких фраз можно охарактеризовать только конечное число натуральных чисел. Пусть  есть «наименьшее из натуральных чисел, которое не характеризуется никакой фразой русского языка, содержащей не более пятидесяти слогов». Взятая в кавычки фраза характеризует число
есть «наименьшее из натуральных чисел, которое не характеризуется никакой фразой русского языка, содержащей не более пятидесяти слогов». Взятая в кавычки фраза характеризует число  и содержит менее пятидесяти слогов.
и содержит менее пятидесяти слогов.
Анализ парадоксов привёл к различным планам их устранения.
Логические парадоксы содержат допущение, что для любого свойства 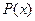 существует соответствующее множество всех элементов
существует соответствующее множество всех элементов 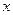 , обладающих свойством
, обладающих свойством 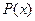 . Если отвергнуть это допущение, то логические парадоксы становятся невозможными. Так, например, парадокс Рассела зависит от существования множества
. Если отвергнуть это допущение, то логические парадоксы становятся невозможными. Так, например, парадокс Рассела зависит от существования множества  всех множеств, которые не является элементами самих себя. Поэтому парадокс Рассела доказывает, что такого множества не существует. Парадоксы Кантора и Бурелли-Форти показывают, что не существует универсального «множества всех множеств» и не существует множества всех ординальных чисел. В 1908 г. Цермело построил аксиоматическую теорию множеств. В рамках этой теории логические парадоксы невозможны, а семантические парадоксы даже невозможно сформулировать.
всех множеств, которые не является элементами самих себя. Поэтому парадокс Рассела доказывает, что такого множества не существует. Парадоксы Кантора и Бурелли-Форти показывают, что не существует универсального «множества всех множеств» и не существует множества всех ординальных чисел. В 1908 г. Цермело построил аксиоматическую теорию множеств. В рамках этой теории логические парадоксы невозможны, а семантические парадоксы даже невозможно сформулировать.
Более глубокое исследование парадоксов было предпринято конструктивистами (Брауэр) и интуиционистами (Гейтинг). С их точки зрения, объект, обладающий некоторыми свойствами, существует только тогда, когда указан метод построения, отыскания такого объекта.
Однако какой бы подход не был избран к проблеме парадоксов, необходимо исследовать язык логики и математики, чтобы разобраться, какие допустимы символы, как из них составлять формулы, утверждения и доказательства, что может и что не может быть доказано, если исходить из различных аксиом и правил вывода. В этом состоянии одна из задач математической логики.
Математическая логика – это обширная наука, которая кроме традиционной проблематики занимается вопросами оснований математики и теории алгоритмов и имеет целый ряд приложений.
Так, Дж. Буль в своих работах сделал попытку свести логику (вернее логику высказываний) к алгебраическим формам, установив систему аксиом символической логики высказываний, которая определила, тем самым методы исследования и решения «логических уравнений». Создание алгебры логики явилось попыткой разрешить традиционные задачи логики чисто алгебраическими методами. Логическое исчисление Дж. Буля стали называть «булевой алгеброй».
Следует заметить, что логика Буля основывается на отношении эквивалентности, при котором левая часть равенства всегда содержит ровно столько же истины, сколько и правая. Следовательно, такая логика не привносит нисколько нового знания. Логика высказываний и логика предикатов (две другие части математической логики) построены на отношении порядка, при котором правая часть логического выражения (заключение) содержит уже больше истины, чем левая (посылка).
В дальнейшем идеи Дж. Буля были развиты, было также показано, что алгебра Буля является частным случаем более общих алгебраических структур, но одновременно «булева алгебра» нашла свое широкое применение в моделировании технических систем, в управлении и стала основой в разработке компьютерных дискретных систем.
Еще раз вернемся к истокам логики как науки. С древнейших времен человечеству известна логика, или искусство правильно рассуждать. Вообще, способность к рассуждениям – это именно искусство. Имея какие-то утверждения (посылки), истинность которых проверена, скажем, на опыте логики, путем умозрительных построений приходит к другому утверждению (заключению), которое также оказывается истинным (в некоторых случаях). Опыт древних (чисто наблюдательный) был систематизирован Аристотелем. Он рассмотрел конкретные виды рассуждений, которые назвал силлогизмами. А именно, Аристотель рассмотрел так называемые категорические утверждения четырех видов:
а) все А обладают свойством В (все А суть В);
б) некоторые A обладают свойством В (некоторые А суть В);
в) все А не обладают свойством В (все А суть не В);
г) некоторые А не обладают свойством В (некоторые A суть не В)
и зафиксировал все случаи, когда из посылок такого вида выводятся заключения одного из этих же видов.
Например:
1. Все люди смертны. Сократ – человек. Следовательно, Сократ смертен. Это рассуждение правильно, потому что подходит под один из образцов силлогизмов Аристотеля.
2. Все дикари раскрашивают свои лица. Некоторые современные женщины раскрашивают свои лица. Следовательно, некоторые современные женщины – дикари. Это рассуждение неправильно, хотя, видимо, все входящие в него утверждения истинны.
Логика Аристотеля – это классическая логика, то есть наука, традиционно относящаяся к гуманитарному циклу наук.
Предметом дальнейшего изложения являются элементы математической логики, а именно логики высказываний и логики предикатов, которые в отличие от алгебры логики Буля являются источником новых истин, привносящих исследователю новые знания.
Основные понятия и определения алгебры
Высказываний.
В данном параграфе будет рассмотрена наиболее простая (элементарная) часть логики.
Определение 1:Высказыванием будем называть простое повествовательное предложение, которое что-либо утверждает и может быть либо истинным, либо ложным. Например, предложение: «Луганск стоит на берегу реки Лугань» – истинное высказывание, а «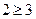 » – ложное.
» – ложное.
Определение 2: Высказывание, для которого никакая его часть не является высказыванием, называется простым или элементарным высказыванием, или атомом.
Из простых высказываний с помощью логических операций можно получать составные или сложные высказывания. Мы будем обозначать высказывания заглавными буквами 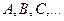 или буквами с индексами.
или буквами с индексами.
Определение 3: Под значением высказывания понимают его истинностное значение (т. е. ложь или истина).
Рассмотрим логические операции над высказываниями. К основным логическим операциям относятся следующие:
Отрицание – обозначается ,читается:«не » или «неверно, что ».
3) Конъюнкция (логическое умножение), обозначаемое (читается «и »). 4) Импликация – обозначается или (читается «из следует», «если , то », «влечёт… 5) Эквивалентность – обозначается или (читается «равносильно », «тогда и только тогда, когда », «для необходимо и…Упражнения для самостоятельной работы.
P = «Данное число – целое», Q = «Данное число – положительное», R = «Данное число – простое»,Формулы алгебры логики. Тавтологии.
Из пропозиционных букв, логических операций и скобок можно составлять различные выражения; некоторые из них называются формулами. Определение 1: Формулами исчисления высказываний являются: а) каждая пропозиционная буква;Доказательство.
Достаточность: Пусть формула в условии теоремы есть тавтология, тогда для любого набора значений пропозиционных переменных, например, , ,..., её… Основная цель в логике высказываний – это поиск тавтологий (общезначимых или… Рассмотрим несколько правил построения новых тавтологий из уже существующих. Зная ограниченное число простых…Упражнения для самостоятельной работы.
1. Определить, является ли данная последовательность символов формулой: 1) 2)Совершенные нормальные конъюнктивные и дизъюнктивные формы. Полные системы логических связок.
Определение 2: Элементарной дизъюнкцией называется дизъюнкция переменных, каждая из которых стоит под знаком отрицания или без него. Например: , .Определение 3: Формула, представленная в виде дизъюнкции элементарных конъюнкций, называется совершенной нормальной дизъюнктивной формой (СНДФ).
Определение 4: Формула, представленная в виде конъюнкции элементарных дизъюнкций, называется совершенной нормальной конъюнктивной формой (СНКФ).
СНДФ и СНКФ можно составлять для данной формулы, пользуясь её таблицей истинности. Рассмотрим таблицу истинности для произвольной формулы алгебры высказываний… ... ... ... ... ... ... …Алгоритм преобразования произвольной формулы в СНДФ.
2) Используя дистрибутивные законы, преобразовать формулу так, чтобы все конъюнкции выполнялись раньше дизъюнкций, а отрицания относились только к… 3) Если имеется несколько одинаковых элементарных конъюнкций, то оставляем… 4) Если в некоторую элементарную конъюнкцию входит переменная со своим отрицанием, то удаляем эту конъюнкцию (, а ). …Замечание о представлении произвольной формулы многочленом Жегалкина.
Введём следующие обозначения: , . Тогда конъюнкция станет обычным умножением символов и . Действительно: …Упражнения для самостоятельной работы.
1. Привести к СНДФ данные формулы: 1) , 2) ,Логика предикатов. Основные понятия и
Определения.
В математике принято одной и той же буквой обозначать различные объекты, т. е. под буквой фактически понимается переменная, принимающая значения из… В логике часто встречаются выражения, грамматически имеющие форму… Определение 1: - местным предикатом, определенным на некотором множестве , называется выражение, содержащее предметные…Определение 3: Множество всех значений таких, что предикат при этих значениях принимает значение «истина», называется областью истинности предиката.
В этом случае область истинности предиката совпадает с множеством . Определение 5: Предикат , определённый на множестве , называется тождественно… В данном случае область истинности предиката – есть пустое множество.Операции над предикатами.
Так как для любого набора значений переменных из области определения предиката он превращается в высказывание, то на множестве предикатов определены те же логические операции, что и для высказываний. При этом от содержания предикатов отвлекаются. Предикаты рассматриваются только с точки зрения их значения. Другими словами, равносильные предикаты не различаются.
Определение 1: Отрицанием  - местного предиката
- местного предиката 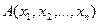 , определенного на множестве
, определенного на множестве  , называется новый
, называется новый  - местный предикат, определенный на том же множестве. Обозначается:
- местный предикат, определенный на том же множестве. Обозначается: 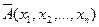 . Читается: «неверно, что
. Читается: «неверно, что 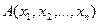 ». Предикат
». Предикат 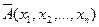 принимает значение «истина» только для тех аргументов, для которых значение предиката
принимает значение «истина» только для тех аргументов, для которых значение предиката 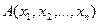 есть «ложь» и наоборот. Другими словами предикат
есть «ложь» и наоборот. Другими словами предикат 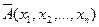 удовлетворяется теми и только теми аргументами, которые не удовлетворяют данному предикату
удовлетворяется теми и только теми аргументами, которые не удовлетворяют данному предикату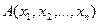 .
.
Двуместный предикат 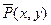 принимает значение «истина» для тех и только тех значений переменных
принимает значение «истина» для тех и только тех значений переменных 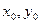 из области определения предиката, для которых предикат
из области определения предиката, для которых предикат 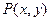 принимает значение «ложь», т. е.
принимает значение «ложь», т. е. 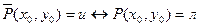 .
.
Определение 2: Конъюнкцией  - местного предиката
- местного предиката 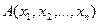 , определенного на множестве
, определенного на множестве  , и
, и 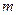 - местного предиката
- местного предиката 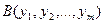 , определенного на множестве
, определенного на множестве 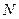 , называется новый
, называется новый 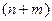 - местный предикат, определенный на множестве
- местный предикат, определенный на множестве 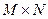 , обозначаемый
, обозначаемый 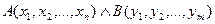 . Читается: «
. Читается: «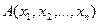 и
и 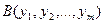 ». Этот предикат принимает значение «истина» только для тех значений аргументов
». Этот предикат принимает значение «истина» только для тех значений аргументов 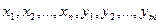 , для которых предикаты
, для которых предикаты 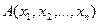 и
и 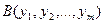 одновременно принимают значение «истина».
одновременно принимают значение «истина».
Если, например, 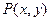 - двуместный предикат, определённый на множестве
- двуместный предикат, определённый на множестве 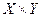 , а
, а 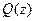 - одноместный предикат, определённый на множестве
- одноместный предикат, определённый на множестве 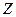 , то конъюнкция этих предикатов
, то конъюнкция этих предикатов 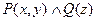 есть трёхместный предикат, определённый на множестве
есть трёхместный предикат, определённый на множестве 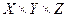 . Этот новый предикат принимает значение «истина» для таких троек элементов
. Этот новый предикат принимает значение «истина» для таких троек элементов 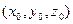 ,
, 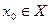 ,
, 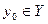 ,
, 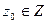 , для которых
, для которых 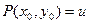 и
и 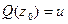 .
.
Аналогично определяются дизъюнкция, импликация и эквивалентность предикатов. Значения предикатов при заданных значениях свободных переменных определяются в соответствии с конкретными логическими операциями. Операции 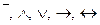 можно применять также к предикатам, у которых имеются общие переменные. В таком случае число переменных полученного составного предиката будет равняться числу различных переменных у его членов. В частности, если операции
можно применять также к предикатам, у которых имеются общие переменные. В таком случае число переменных полученного составного предиката будет равняться числу различных переменных у его членов. В частности, если операции 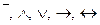 применяются к двум
применяются к двум  - местным предикатам, зависящим от одних и тех же переменных, то в результате применения логических операций получается
- местным предикатам, зависящим от одних и тех же переменных, то в результате применения логических операций получается  - местный предикат, зависящий от тех же переменных.
- местный предикат, зависящий от тех же переменных.
Пусть 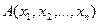 и
и 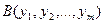 – два
– два  - местных предиката, зависящих от одних и тех же переменных. Тогда:
- местных предиката, зависящих от одних и тех же переменных. Тогда:
а) множество истинности конъюнкции 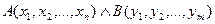 равно пересечению множеств истинности ее членов;
равно пересечению множеств истинности ее членов;
б) множество истинности дизъюнкции 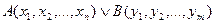 равно объединению множеств истинности ее членов.
равно объединению множеств истинности ее членов.
Не трудно показать, что конъюнкция двух предикатов тождественно истинна тогда и только тогда, когда оба данных предиката тождественно истинны. Дизъюнкция двух предикатов выполнима тогда и только тогда, когда, по крайней мере, один из них выполним. Дизъюнкция двух предикатов тождественно ложна тогда и только тогда, когда оба данных предиката тождественно ложны. Импликация двух  - местных предикатов зависящих от одних и тех же аргументов, тождественно истинна тогда и только тогда, когда ее заключение является следствием посылки. Эквивалентность двух
- местных предикатов зависящих от одних и тех же аргументов, тождественно истинна тогда и только тогда, когда ее заключение является следствием посылки. Эквивалентность двух  - местных предикатов, зависящих от одних и тех же переменных тождественно истинна тогда и только тогда, когда оба предиката равносильны.
- местных предикатов, зависящих от одних и тех же переменных тождественно истинна тогда и только тогда, когда оба предиката равносильны.
Всякое уравнение (неравенство), содержащее переменные, является предикатом, определённым на том же множестве, на котором задано уравнение (неравенство). Множество решений уравнения (неравенства) есть ничто иное, как множество истинности предиката. Это означает, что при подстановке корней уравнения (или решений неравенства) вместо неизвестных будут получены истинные высказывания. Если же в уравнение (неравенство) вместо переменных подставлять числа, не являющиеся решениями, то будут получены ложные высказывания. Всякая система уравнений (неравенств) может быть рассмотрена, как конъюнкция предикатов. Решить систему – значит найти область истинности конъюнкции предикатов. Совокупность уравнений (неравенств) есть ничто иное, как дизъюнкция предикатов. Равносильность уравнений (неравенств) означает равносильность соответствующих предикатов.
Если 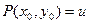 , то говорят, что аргумент
, то говорят, что аргумент 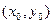 удовлетворяет данному предикату. Например, число 3 удовлетворяет предикату
удовлетворяет данному предикату. Например, число 3 удовлетворяет предикату 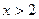 , а число 1 ему не удовлетворяет.
, а число 1 ему не удовлетворяет.
В математической логике кроме логических операций над предикатами, существуют операции квантификации, которые делают логику предикатов значительно богаче по содержанию в сравнении с логикой высказываний. При этом, как и в случае простейших операций, предикаты рассматриваются только сточки зрения их значений, т.е. равносильные предикаты не различаются. Основными кванторными операциями являются: квантор общности и квантор существования, которые являются двойственными друг для друга.
Определение 3: Пусть  - одноместный предикат, определенный на непустом множестве
- одноместный предикат, определенный на непустом множестве 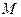 . Операция, превращающая предикат
. Операция, превращающая предикат  в высказывание:
в высказывание: 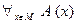 (читается: «для любого
(читается: «для любого 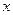 выполняется
выполняется  »), называется квантором общности (или универсальным высказыванием). Высказывание
»), называется квантором общности (или универсальным высказыванием). Высказывание 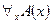 истинно тогда и только тогда, когда данный предикат
истинно тогда и только тогда, когда данный предикат  тождественно истинный (т. е. область истинности предиката
тождественно истинный (т. е. область истинности предиката  совпадает с множеством
совпадает с множеством 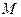 ).
).
Символ 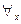 называется квантором общности по переменой
называется квантором общности по переменой  , его читают: «для всех
, его читают: «для всех  » или «для каждого
» или «для каждого ». Говорят, что высказывание
». Говорят, что высказывание 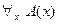 есть результат применения квантора общности к предикату
есть результат применения квантора общности к предикату . Символ
. Символ 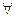 происходит от английского слова «All» (в переводе: «все»).
происходит от английского слова «All» (в переводе: «все»).
Например, для предикатов «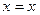 » и «
» и «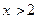 », определенных на множестве действительных чисел, соответствующие универсальные высказывания будут иметь вид:
», определенных на множестве действительных чисел, соответствующие универсальные высказывания будут иметь вид: 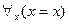 – «каждое действительное число равно самому себе» (истинное) и
– «каждое действительное число равно самому себе» (истинное) и 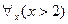 – «каждое действительное число больше 2» (ложное).
– «каждое действительное число больше 2» (ложное).
Теорема 1: Если  - одноместный предикат, определенный на конечном множестве, состоящем из
- одноместный предикат, определенный на конечном множестве, состоящем из 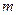 элементов
элементов 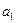 ,
,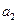 ,…,
,…,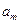 , то соответствующее ему универсальное высказывание эквивалентно конъюнкции
, то соответствующее ему универсальное высказывание эквивалентно конъюнкции 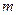 высказываний
высказываний 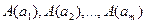 :
:
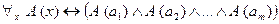 .
.
Доказательство. В самом деле, согласно определению квантора общности, высказывание 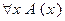 будет истинным тогда и только тогда, когда предикат
будет истинным тогда и только тогда, когда предикат  тождественно истинный, т.е. когда истинны все
тождественно истинный, т.е. когда истинны все 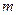 высказываний
высказываний 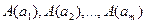 , получаемые из данного предиката заменой переменного
, получаемые из данного предиката заменой переменного  аргументами
аргументами 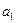 ,
,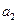 ,…,
,…,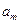 соответственно. Последнее замечание возможно в том и только том случае, когда истинна конъюнкция этих
соответственно. Последнее замечание возможно в том и только том случае, когда истинна конъюнкция этих 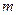 высказываний. Т.е. члены эквивалентности одновременно истинны или ложны, а, следовательно, эквивалентность доказана.
высказываний. Т.е. члены эквивалентности одновременно истинны или ложны, а, следовательно, эквивалентность доказана.
Теорема показывает, что для предикатов, определенных на конечном множестве, операция применения квантора общности может быть выражена через конъюнкцию. Для предикатов, определенных на бесконечном множестве, это сделать невозможно, в этом случае операция применения квантора общности является абсолютно новой.
Определение4: Пусть  - одноместный предикат, определенный на множестве
- одноместный предикат, определенный на множестве 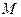 . Операция, превращающая предикат
. Операция, превращающая предикат  в высказывание
в высказывание 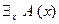 (читается: «существует
(читается: «существует 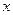 , удовлетворяющее предикату
, удовлетворяющее предикату  »), называется квантором существования (или экзистенциональным высказыванием). Высказывание
»), называется квантором существования (или экзистенциональным высказыванием). Высказывание 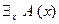 будет истинным тогда и только тогда, когда предикат
будет истинным тогда и только тогда, когда предикат  выполнимый. Это высказывание будет ложным, если предикат
выполнимый. Это высказывание будет ложным, если предикат  тождественно ложный.
тождественно ложный.
Символ 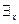 называется квантором существования по переменной
называется квантором существования по переменной  . Его можно прочитать: «существует
. Его можно прочитать: «существует  такой, что
такой, что  », или «найдётся такой
», или «найдётся такой  , что
, что  ». Говорят, что высказывание
». Говорят, что высказывание 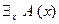 - есть результат применения квантора к предикату
- есть результат применения квантора к предикату  . Например, для предикатов «
. Например, для предикатов «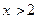 » и «
» и «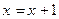 », определенных на множестве действительных чисел, соответствующие экзистенциональные высказывания будут иметь вид:
», определенных на множестве действительных чисел, соответствующие экзистенциональные высказывания будут иметь вид: 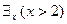 – «существует действительное число, большее 2» (истинное), и
– «существует действительное число, большее 2» (истинное), и 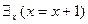 – «существует действительное число
– «существует действительное число  , равное сумме
, равное сумме 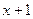 » (ложное). Символ
» (ложное). Символ  происходит от английского слова «Exist» (существует).
происходит от английского слова «Exist» (существует).
Теорема 2: Если  – одноместный предикат, определенный на конечном множестве из
– одноместный предикат, определенный на конечном множестве из 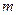 элементов
элементов 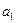 ,
,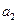 ,…,
,…,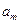 , то соответствующее ему экзистенциональное высказывание эквивалентно дизъюнкции
, то соответствующее ему экзистенциональное высказывание эквивалентно дизъюнкции 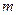 высказываний
высказываний 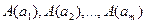 :
:
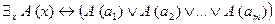 .
.
Доказательство: По определению: высказывание 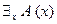 будет ложно тогда и только тогда, когда ложны все
будет ложно тогда и только тогда, когда ложны все 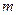 высказываний
высказываний 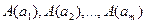 , которые получаются из данного предиката при замене переменной
, которые получаются из данного предиката при замене переменной  аргументами
аргументами 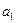 ,
,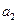 ,…,
,…,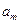 соответственно. Последнее замечание возможно в том и только в том случае, когда ложна дизъюнкция этих
соответственно. Последнее замечание возможно в том и только в том случае, когда ложна дизъюнкция этих 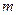 высказываний. Т.е. члены эквивалентности одновременно истинны или ложны, следовательно, эта эквивалентность истинна.
высказываний. Т.е. члены эквивалентности одновременно истинны или ложны, следовательно, эта эквивалентность истинна.
Эта теорема утверждает, что для предикатов, определенных на конечных множествах, операция применения квантора существования может быть выражена через дизъюнкцию. Для предикатов, определенных на бесконечных множествах, это сделать невозможно. Операция применения квантора существования тогда является абсолютно новой.
Следует запомнить, что для любого предиката  , определенного на множестве
, определенного на множестве 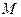 выражения
выражения  и
и 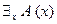 – это высказывания, а не предикаты. Присутствие переменной
– это высказывания, а не предикаты. Присутствие переменной  здесь чисто внешнее, связанное со способом обозначений. Поэтому переменная
здесь чисто внешнее, связанное со способом обозначений. Поэтому переменная  , входящая в выражения
, входящая в выражения  и
и 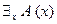 , называется связанной переменной, в отличие от переменной, входящей в предикат
, называется связанной переменной, в отличие от переменной, входящей в предикат  , где переменная называется свободной. Если применить операцию «навешивания» кванторов двуместному предикату
, где переменная называется свободной. Если применить операцию «навешивания» кванторов двуместному предикату 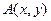 по какой-нибудь переменной, то в результате двуместный предикат превратится в одноместный предикат с одной свободной переменной. Аналогичные рассуждения можно провести для второй переменной. Переменная, по которой был применён квантор, называется связной переменной. Если применить кванторную операцию к
по какой-нибудь переменной, то в результате двуместный предикат превратится в одноместный предикат с одной свободной переменной. Аналогичные рассуждения можно провести для второй переменной. Переменная, по которой был применён квантор, называется связной переменной. Если применить кванторную операцию к  - местному предикату по какой-нибудь переменной, то он превратится в
- местному предикату по какой-нибудь переменной, то он превратится в 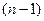 - местный предикат.
- местный предикат.
Если в любом предикате все переменные связаны, то этот предикат является высказыванием. Например, рассмотрим предикат 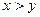 , определённый на некотором числовом множестве. Составим высказывание
, определённый на некотором числовом множестве. Составим высказывание  . Это ложное высказывание, которое утверждает, что найдётся такое число
. Это ложное высказывание, которое утверждает, что найдётся такое число 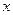 , которое больше всякого числа
, которое больше всякого числа  (
(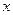 - единственное число для всех
- единственное число для всех  ). Поменяв местами кванторы, получим новое высказывание:
). Поменяв местами кванторы, получим новое высказывание: 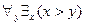 . Это высказывание утверждает, что для любого числа
. Это высказывание утверждает, что для любого числа  можно подобрать такое число
можно подобрать такое число 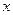 , что выполняется неравенство
, что выполняется неравенство 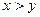 (для каждого
(для каждого  существует своё число
существует своё число 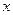 ). Это высказывание истинно. Видно, что при перестановке кванторов местами меняется смысл высказывания. Таким образом, перестановка разноимённых кванторов местами является недопустимой операцией. Одноимённые кванторы местами менять можно. Причем, одноимённые кванторы можно объединять в один, например:
). Это высказывание истинно. Видно, что при перестановке кванторов местами меняется смысл высказывания. Таким образом, перестановка разноимённых кванторов местами является недопустимой операцией. Одноимённые кванторы местами менять можно. Причем, одноимённые кванторы можно объединять в один, например: 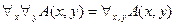 . Недопустимым является также применение нескольких кванторов по одной и той же переменной, например:
. Недопустимым является также применение нескольких кванторов по одной и той же переменной, например: 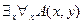 .
.
Определение 5: Универсальным высказыванием, соответствующим  - местному предикату
- местному предикату  , определенному на множестве
, определенному на множестве  , называется высказывание, полученное из предиката
, называется высказывание, полученное из предиката  последовательным применением
последовательным применением  кванторов общности по переменным
кванторов общности по переменным 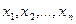 в любом порядке.
в любом порядке.
Обозначается такое высказывание 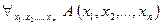 и читается кратко так: «для всех
и читается кратко так: «для всех  выполняется
выполняется  ».
».
Определение 6: Экзистенциональным высказыванием, соответствующим  - местному предикату
- местному предикату  , определенному на множестве
, определенному на множестве  , называется высказывание, полученное из предиката
, называется высказывание, полученное из предиката  последовательным применением
последовательным применением  кванторов существования по переменным
кванторов существования по переменным 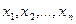 в любом порядке.
в любом порядке.
Полученное экзистенциональное высказывание обозначают 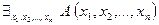 и читают так: «существует такой набор
и читают так: «существует такой набор 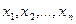 , что выполняется
, что выполняется  ».
».
Например, для двуместного предиката «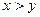 » соответствующие высказывания имеют вид:
» соответствующие высказывания имеют вид: 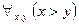 – «для любых двух действительных чисел: первое больше второго» (ложное), и
– «для любых двух действительных чисел: первое больше второго» (ложное), и 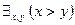 – «существуют два действительных числа, из которых первое больше второго» (истинное).
– «существуют два действительных числа, из которых первое больше второго» (истинное).
Теорема 3: (Условие тождественной истинности квантифицированного предиката).
 ‑ местный предикат, полученный из
‑ местный предикат, полученный из  ‑ местного предиката
‑ местного предиката  , определенного на множестве
, определенного на множестве  , применением квантора общности по какой-либо переменной является тождественно истинным тогда и только тогда, когда данный предикат
, применением квантора общности по какой-либо переменной является тождественно истинным тогда и только тогда, когда данный предикат  – тождественно истинный.
– тождественно истинный.
Доказательство: Действительно, пусть дан  - местный предикат
- местный предикат  , определенный на множестве
, определенный на множестве  . По определению, этот предикат будет тождественно истинным тогда и только тогда, когда его значение для произвольно взятых значений аргументов есть «истина». Это значит, что истинным является универсальное высказывание
. По определению, этот предикат будет тождественно истинным тогда и только тогда, когда его значение для произвольно взятых значений аргументов есть «истина». Это значит, что истинным является универсальное высказывание 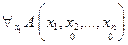 , соответствующее одноместному предикату
, соответствующее одноместному предикату 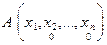 , определенному на множестве
, определенному на множестве  . Последнее замечание возможно тогда и только тогда, когда предикат
. Последнее замечание возможно тогда и только тогда, когда предикат 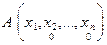 – тождественно истинный, но т.к. аргументы
– тождественно истинный, но т.к. аргументы 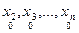 выбирались произвольно, то это равносильно тождественной истинности данного
выбирались произвольно, то это равносильно тождественной истинности данного  - местного предиката
- местного предиката  . Теорема доказана.
. Теорема доказана.
Теорема 4: (Условие тождественной ложности квантифицированного предиката).
 -местный предикат, полученный из
-местный предикат, полученный из  - местного предиката
- местного предиката  , определенного на множестве
, определенного на множестве  , применением квантора существования по какой-либо переменной, тождественно ложен тогда и только тогда, когда данный предикат тождественно ложен.
, применением квантора существования по какой-либо переменной, тождественно ложен тогда и только тогда, когда данный предикат тождественно ложен.
Доказательство: Пусть имеем  - местный предикат
- местный предикат 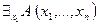 , определенный на множестве
, определенный на множестве  . Он будет тождественно ложен тогда и только тогда, когда его значение для произвольно взятых аргументов
. Он будет тождественно ложен тогда и только тогда, когда его значение для произвольно взятых аргументов 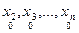 есть «ложь». Это значит, что ложно экзистенциональное высказывание
есть «ложь». Это значит, что ложно экзистенциональное высказывание 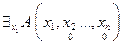 , соответствующее одноместному предикату
, соответствующее одноместному предикату 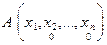 , определенному на множестве
, определенному на множестве  . Последнее возможно в том и только в том случае, когда предикат
. Последнее возможно в том и только в том случае, когда предикат 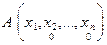 тождественно ложен, а т.к. аргументы
тождественно ложен, а т.к. аргументы 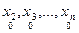 выбирались произвольно, то и данный
выбирались произвольно, то и данный  - местный предикат
- местный предикат  тождественно ложен. Что и требовалось доказать.
тождественно ложен. Что и требовалось доказать.
До сих пор мы противопоставляли предикаты высказываниям. Однако удобнее считать высказывания 0 ‑ местными предикатами. Тогда любые два истинные и любые два ложных высказывания следует считать равносильными между собой. Каждое истинное высказывание будет тогда тождественно истинным 0-местным предикатом, а каждое ложное высказывание – тождественно ложный 0-местный предикат. Тогда по определению, если  – высказывание, то имеют место эквивалентности:
– высказывание, то имеют место эквивалентности: 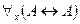 и
и 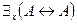 .
.
Упражнения для самостоятельной работы.
1) ; 4) ; 2) ; 5) . 3) ;Формулы и тавтологии логики предикатов.
При введении определения формул логики предикатов будем использовать следующие… 1) – индивидные переменные,Упражнения для самостоятельной работы.
1. Записать следующие высказывания в виде формул логики предикатов. 1) Всякое натуральное число, делящееся на 12, делится на 2, 4 и 6. 2) Жители Швейцарии обязательно владеют французским, или итальянским, или немецким языком.Логическая структура теоремы.
Некоторые схемы доказательства теорем.
Многие теоремы в математике имеют форму импликации . В этом случае условие… Рассмотрим для примера известную из планиметрии теорему: «Если в треугольнике боковые стороны равны, то в этом…Рассмотрим некоторые схемы доказательства теорем.
Доказательство можно построить по следующей схеме: выбрать элемент такой, что . Исходя из конкретных условий теоремы, доказывают, что из истинности… 2) Схема доказательства, основанная на законе силлогизма: .Упражнения для самостоятельной работы.
1.Записать на языке логики предикатов аксиому математической индукции. 2. Записать на языке логики предикатов следующую теорему арифметики: «НОД чисел и можно представить, как линейную…Формальный язык логики высказываний.
Таблицы истинности в логике высказываний позволяют ответить на многие вопросы. Например, является ли данная формула тавтологией, противоречием или… Исторически понятие формальной теории было разработано в период интенсивных… Определение 1: Формальная (аксиоматическая) теория считается определенной, если выполнены следующие условия:Определение 4: Формула называется следствием формул множества тогда и только тогда, когда существует такая последовательность формул , что . И для каждого формула является либо аксиомой, либо формулой из множества , либо непосредственным следствием некоторых предыдущих формул по одному из правил вывода. Такая последовательность называется выводом из множества . Формулы из множества называются гипотезами, или посылками вывода.
Для краткой записи утверждения « является следствием
является следствием  » будем использовать обозначение:
» будем использовать обозначение:  ├
├ . Если множество
. Если множество  конечно, т. е.
конечно, т. е. 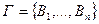 , будем писать:
, будем писать: 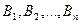 ├
├ . Если
. Если  - пустое множество, то
- пустое множество, то  ├
├ имеет место тогда и только тогда, когда
имеет место тогда и только тогда, когда  является теоремой. В этом случае принято писать: ├
является теоремой. В этом случае принято писать: ├ . Эта запись означает, что
. Эта запись означает, что  - теорема.
- теорема.
Приведём простые свойства выводимости из посылок.
1) Если 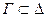 и
и  ├
├ , то
, то  ├
├ .
.
Т. е., если  выводимо из множества посылок
выводимо из множества посылок  , то
, то  останется выводимым, если добавить в
останется выводимым, если добавить в  новые посылки.
новые посылки.
2)  ├
├ тогда и только тогда, когда в
тогда и только тогда, когда в  найдётся конечное подмножество
найдётся конечное подмножество  , для которого
, для которого  ├
├ .
.
Это утверждение вытекает из предыдущего и из того факта, что всякое доказательство содержит конечное число формул.
3) Если  ├
├ и
и  ├
├ для любого
для любого  из
из  , то
, то  ├
├ .
.
Смысл этого утверждения состоит в том, что если  выводимо из
выводимо из  и каждая формула, содержащаяся в
и каждая формула, содержащаяся в  , выводима из
, выводима из  , то
, то  выводимо из
выводимо из  .
.
Теперь перейдём к изложению формальной аксиоматической теории  для исчисления высказываний.
для исчисления высказываний.
1) Алфавитом теории  являются символы:
являются символы:  ,
, 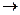 ,
, 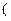 ,
, 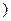 и буквы
и буквы 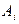 с целыми положительными индексами:
с целыми положительными индексами: 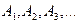 Символы
Символы  и
и 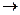 называют примитивными связками (логические операции отрицание и импликация), а буквы
называют примитивными связками (логические операции отрицание и импликация), а буквы 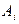 – пропозиционными буквами.
– пропозиционными буквами.
2) а) Каждая пропозиционная буква есть формула.
б) Если  и
и  – формулы, то
– формулы, то 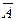 и
и  – тоже формулы.
– тоже формулы.
Таким образом, всякая формула теории  получается из пропозиционных букв с помощью логических операций отрицания и импликации.
получается из пропозиционных букв с помощью логических операций отрицания и импликации.
3) Каковы бы ни были формулы 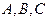 теории
теории  , следующие формулы есть аксиомы в теории
, следующие формулы есть аксиомы в теории  :
:
(А1) 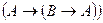 ;
;
(А2) 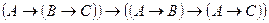 ;
;
(А3) 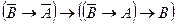 .
.
4) Единственным правилом вывода служит правило modus ponens: « есть непосредственное следствие
есть непосредственное следствие  и
и  ». Это правило называют также правилом отделения, будем его сокращенно обозначать:
». Это правило называют также правилом отделения, будем его сокращенно обозначать:  Далее будем придерживаться соглашений о сокращении числа скобок.
Далее будем придерживаться соглашений о сокращении числа скобок.
Отметим, что бесконечное множество аксиом теории  задано с помощью всего лишь трех схем аксиом
задано с помощью всего лишь трех схем аксиом 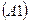 ,
,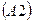 ,
,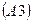 , каждая из которых порождает бесконечное множество аксиом.
, каждая из которых порождает бесконечное множество аксиом.
Мы строим систему  таким образом, чтобы класс всех теорем этой теории совпадал с классом всех тавтологий исчисления высказываний.
таким образом, чтобы класс всех теорем этой теории совпадал с классом всех тавтологий исчисления высказываний.
Введем в рассмотрение остальные логические операции (связки) с помощью следующих определений:
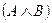 означает
означает 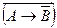 ;
;
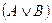 означает
означает 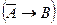 ;
;
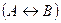 означает
означает 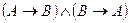 .
.
Другими словами, мы выбираем новые названия для некоторых выражений языка теории  .
.
Замечание: Слово «вывод» (или «доказательство») употребляется в двух различных смыслах. Во-первых, оно употребляется как название конечных последовательностей формул теории  . Во-вторых, оно означает последовательность предложений разговорного языка (дополненного техническими терминами), о которой предполагается, что она служит достаточно обоснованной аргументацией в пользу утверждения о теории
. Во-вторых, оно означает последовательность предложений разговорного языка (дополненного техническими терминами), о которой предполагается, что она служит достаточно обоснованной аргументацией в пользу утверждения о теории  . Мы изучаем язык теории
. Мы изучаем язык теории  с помощью метаязыка. Этот метаязык можно было бы формализовать, но тогда рассуждения о нём нужно было бы проводить в новом метаязыке и т. д.
с помощью метаязыка. Этот метаязык можно было бы формализовать, но тогда рассуждения о нём нужно было бы проводить в новом метаязыке и т. д.
Далее будут рассмотрены теоремы формальной теории  и «метатеоремы» о свойствах этой формальной теории. При изучении формальных теорий нужно различать теоремы формальной теории и теоремы о формальной теории или метатеоремы. Это различие не всегда явно формализуется, но всегда является существенным. В этом параграфе теоремы конкретной формальной теории, как правило, записываются в виде формул, составленных из специальных знаков, а метатеоремы формулируются на естественном языке, чтобы их легче было отличать от теорем самой формальной теории.
и «метатеоремы» о свойствах этой формальной теории. При изучении формальных теорий нужно различать теоремы формальной теории и теоремы о формальной теории или метатеоремы. Это различие не всегда явно формализуется, но всегда является существенным. В этом параграфе теоремы конкретной формальной теории, как правило, записываются в виде формул, составленных из специальных знаков, а метатеоремы формулируются на естественном языке, чтобы их легче было отличать от теорем самой формальной теории.
Теорема 1: Для любой формулы  в теории
в теории  формула
формула 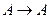 выводима.
выводима.
Доказательство: Построим вывод формулы 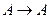 в теории
в теории  .
.
1. 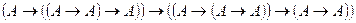 (схема аксиом (А2)).
(схема аксиом (А2)).
2. 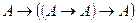 (схема аксиом (А1)).
(схема аксиом (А1)).
3. 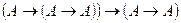 (из 1 и 2 по правилу вывода
(из 1 и 2 по правилу вывода  ).
).
4. 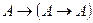 (схема аксиом (А1)).
(схема аксиом (А1)).
5. 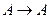 (из 3 и 4 по правилу вывода
(из 3 и 4 по правилу вывода  ).
).
Подобным образом доказываются другие теоремы этой теории.
Теорема 2: (теорема дедукции, Эрбран (1930 г.)).
Если  - множество формул,
- множество формул,  и
и  – формулы и
– формулы и  ,
,  ├
├ , то
, то  ├
├ .
.
В частности, если  ├
├ , то ├
, то ├ .
.
Доказательство: Пусть 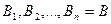 вывод из
вывод из 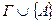 . Докажем, что
. Докажем, что  ├
├ индукцией по
индукцией по 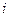
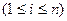 .
.
При 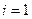 формула
формула 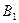 должна быть либо формулой из множества
должна быть либо формулой из множества  , либо аксиомой теории
, либо аксиомой теории  , либо должна совпадать с
, либо должна совпадать с  . По схеме аксиом (А1):
. По схеме аксиом (А1): 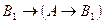 есть аксиома. Поэтому, в первых двух случаях имеем:
есть аксиома. Поэтому, в первых двух случаях имеем:  ├
├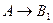 по правилу вывода
по правилу вывода  . В третьем случае, т. е. когда
. В третьем случае, т. е. когда 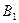 совпадает с
совпадает с  , согласно теореме 1, имеем: ├
, согласно теореме 1, имеем: ├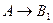 . Следовательно,
. Следовательно,  ├
├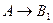 . Таким образом, теорема доказана для случая, когда длина вывода
. Таким образом, теорема доказана для случая, когда длина вывода 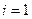 .
.
Пусть  ├
├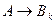 для любого
для любого 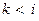 (индуктивное допущение). Для
(индуктивное допущение). Для 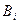 имеем четыре возможности:
имеем четыре возможности: 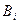 - есть аксиома, или
- есть аксиома, или 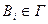 , или
, или 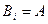 , или
, или 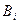 следует из некоторых
следует из некоторых  и
и 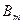 (где
(где 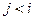 и
и 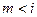 ) по правилу
) по правилу  , т. е. имеет вид:
, т. е. имеет вид: 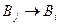 . В трёх первых случаях
. В трёх первых случаях  ├
├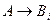 доказывается так же, как для случая
доказывается так же, как для случая 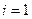 . В последнем случае применим индуктивное допущение, согласно которому
. В последнем случае применим индуктивное допущение, согласно которому  ├
├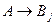 и
и  ├
├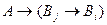 . По схеме аксиом (А2) имеем: ├
. По схеме аксиом (А2) имеем: ├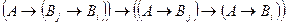 . Следовательно, по правилу вывода
. Следовательно, по правилу вывода  :
:  ├
├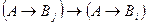 и снова по
и снова по  :
:  ├
├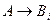 . Доказательство по индукции закончено, и для
. Доказательство по индукции закончено, и для 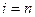 получаем требуемое.
получаем требуемое.
Замечание: Доказательство позволяет по данному выводу  из
из 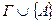 построить вывод
построить вывод  из
из  , причём при доказательстве используются только схемы аксиом (А1) и (А2).
, причём при доказательстве используются только схемы аксиом (А1) и (А2).
Следствие 1: 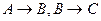 ├
├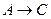 .
.
Доказательство:
1)  - гипотеза.
- гипотеза.
2)  - гипотеза.
- гипотеза.
3)  - гипотеза.
- гипотеза.
4)  - выводится из пунктов 1 и 3 по
- выводится из пунктов 1 и 3 по 
5)  - выводится из пунктов 2 и 4 по
- выводится из пунктов 2 и 4 по 
Таким образом, 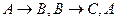 ├
├ . Отсюда по теореме дедукции имеем:
. Отсюда по теореме дедукции имеем: 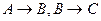 ├
├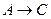 .
.
Следствие 2: 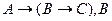 ├
├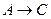 .
.
Доказательство:
1) 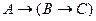 - гипотеза.
- гипотеза.
2)  - гипотеза.
- гипотеза.
3)  - гипотеза.
- гипотеза.
4)  - выводится из пунктов 1 и 3 по
- выводится из пунктов 1 и 3 по 
5)  - выводится из пунктов 4 и 2 по
- выводится из пунктов 4 и 2 по 
Значит, 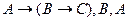 ├
├ . Применяя теорему дедукции, получаем:
. Применяя теорему дедукции, получаем: 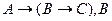 ├
├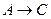 .
.
Теорема 3: ├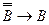 .
.
Доказательство:
1) 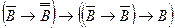 - схема аксиом (А3).
- схема аксиом (А3).
2) 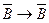 - теорема 1.
- теорема 1.
3)  - следствие 2 из теоремы дедукции, применённое к пунктам 1 и 2.
- следствие 2 из теоремы дедукции, применённое к пунктам 1 и 2.
4) 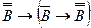 - схема аксиом (А1).
- схема аксиом (А1).
5) 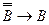 - следствие 1 из теоремы дедукции, применённое к пунктам 4 и 3.
- следствие 1 из теоремы дедукции, применённое к пунктам 4 и 3.
Теорема доказана.
Теорема 4: ├ .
.
Доказательство:
1) 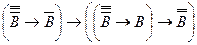 - схема аксиом (А3).
- схема аксиом (А3).
2) 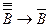 - теорема 3.
- теорема 3.
3) 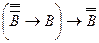 - выводится из пунктов 1 и 2 по правилу вывода
- выводится из пунктов 1 и 2 по правилу вывода  .
.
4) 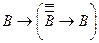 - схема аксиом (А1).
- схема аксиом (А1).
5)  - следствие 1 из теоремы дедукции, применённое к пунктам 4 и 3.
- следствие 1 из теоремы дедукции, применённое к пунктам 4 и 3.
Теорема доказана.
Замечание (метаязык): Из теорем 3 и 4 следует, что в теории  доказан закон двойного отрицания.
доказан закон двойного отрицания.
Теорема 5: ├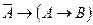 .
.
Доказательство:
1) 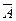 - гипотеза.
- гипотеза.
2)  - гипотеза.
- гипотеза.
3) 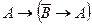 - схема аксиом (А1).
- схема аксиом (А1).
4) 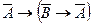 - схема аксиом (А1).
- схема аксиом (А1).
5) 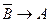 - выводится из пунктов 3 и 2 по правилу modus ponens.
- выводится из пунктов 3 и 2 по правилу modus ponens.
6) 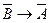 - выводится из пунктов 4 и 1 по правилу modus ponens.
- выводится из пунктов 4 и 1 по правилу modus ponens.
7) 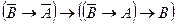 - схема аксиом (А3).
- схема аксиом (А3).
8)  - выводится из пунктов 6 и 7 по правилу modus ponens.
- выводится из пунктов 6 и 7 по правилу modus ponens.
9)  - выводится из пунктов 5 и 8 по правилу modus ponens.
- выводится из пунктов 5 и 8 по правилу modus ponens.
Итак, доказано, что  ├
├ . Применяя дважды теорему дедукции, получим:
. Применяя дважды теорему дедукции, получим: 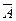 ├
├ и ├
и ├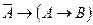 . Что и требовалось доказать.
. Что и требовалось доказать.
Замечание (метаязык): Доказанная теорема в содержательной логике означает, что из  и
и 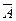 , т. е. из любого противоречия, логически следует любое высказывание
, т. е. из любого противоречия, логически следует любое высказывание  . Таким образом, следствием противоречия является вся «мудрость мира и все глупости», т. е. высказывания
. Таким образом, следствием противоречия является вся «мудрость мира и все глупости», т. е. высказывания 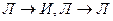 являются истинными.
являются истинными.
Теорема 6: ├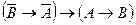 .
.
Доказательство:
1) 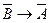 - гипотеза.
- гипотеза.
2)  - гипотеза.
- гипотеза.
3) 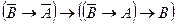 - схема аксиом (А3).
- схема аксиом (А3).
4) 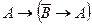 - схема аксиом (А1).
- схема аксиом (А1).
5)  - выводится из пунктов 1 и 3 по правилу modus ponens.
- выводится из пунктов 1 и 3 по правилу modus ponens.
6)  - следствие 1 из теоремы дедукции, применённое к пунктам 4 и 5.
- следствие 1 из теоремы дедукции, применённое к пунктам 4 и 5.
7)  - выводится из пунктов 2 и 6 по правилу modus ponens.
- выводится из пунктов 2 и 6 по правилу modus ponens.
Таким образом, 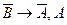 ├
├ . Применяя дважды теорему дедукции, получаем:
. Применяя дважды теорему дедукции, получаем: 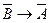 ├
├ . И, наконец, ├
. И, наконец, ├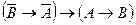 . Что и требовалось доказать.
. Что и требовалось доказать.
Теорема 7: ├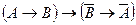 .
.
Доказательство:
1)  - гипотеза.
- гипотеза.
2) 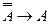 - теорема 3.
- теорема 3.
3) 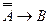 - следствие 1 из теоремы дедукции, применённое к пунктам 2 и 1.
- следствие 1 из теоремы дедукции, применённое к пунктам 2 и 1.
4)  - теорема 4.
- теорема 4.
5) 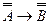 - следствие 1 из теоремы дедукции, применённое к пунктам 3 и 4.
- следствие 1 из теоремы дедукции, применённое к пунктам 3 и 4.
6) 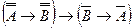 - теорема 6.
- теорема 6.
7) 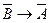 - выводимо из пунктов 5 и 6 по правилу modus ponens.
- выводимо из пунктов 5 и 6 по правилу modus ponens.
Таким образом, доказано, что  ├
├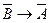 , откуда по теореме дедукции имеем: ├
, откуда по теореме дедукции имеем: ├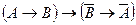 . Теорема доказана.
. Теорема доказана.
Замечание: Из теорем 6 и 7 следует закон контрапозиции в теории  .
.
Теорема 8: ├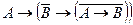 .
.
Доказательство: Правило modus ponens можно записать следующим образом: 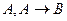 ├
├ . Применяя дважды теорему дедукции, получим:
. Применяя дважды теорему дедукции, получим:
├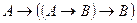 . (а)
. (а)
По теореме 7 имеем:
├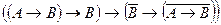 . (б)
. (б)
Теперь по следствию 1 из теоремы дедукции, применённому к пунктам (а) и (б), получаем: ├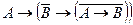 . Что и требовалось доказать.
. Что и требовалось доказать.
Теорема 9: ├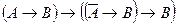 .
.
Доказательство:
1)  - гипотеза.
- гипотеза.
2) 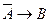 - гипотеза.
- гипотеза.
3) 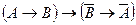 - теорема 7.
- теорема 7.
4) 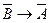 - выводится из пунктов 1 и 3 по правилу
- выводится из пунктов 1 и 3 по правилу  .
.
5) 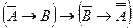 - теорема 6.
- теорема 6.
6) 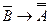 - выводится из пунктов 2 и 5 по правилу
- выводится из пунктов 2 и 5 по правилу  .
.
7) 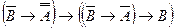 - схема аксиом (А3).
- схема аксиом (А3).
8)  - выводится из пунктов 6 и 7 по правилу
- выводится из пунктов 6 и 7 по правилу  .
.
9)  - выводится из пунктов 4 и 8 по правилу
- выводится из пунктов 4 и 8 по правилу  .
.
Итак, 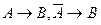 ├
├ . Применяя два раза теорему дедукции, получаем утверждение теоремы: ├
. Применяя два раза теорему дедукции, получаем утверждение теоремы: ├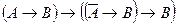 .
.
Замечание: Доказанной теореме в содержательной логике соответствует тот факт, что если  выводимо из
выводимо из  и
и  выводимо из
выводимо из 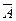 , то
, то  - истинно (
- истинно (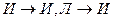 ).
).
Наша дальнейшая цель – показать, что произвольная формула теории  тогда и только тогда является теоремой этой теории, когда она есть тавтология.
тогда и только тогда является теоремой этой теории, когда она есть тавтология.
Теорема 10 (метатеорема): Всякая теорема теории  есть тавтология.
есть тавтология.
Доказательство прямого утверждения очень простое. Для примера можно убедиться в том, что каждая аксиома теории  есть тавтология. Кроме того, если
есть тавтология. Кроме того, если  и
и  – тавтологии, то и
– тавтологии, то и  является тавтологией. Таким образом, правило modus ponens, примененное к тавтологиям, приводит к тавтологиям. Следовательно, всякая теорема теории
является тавтологией. Таким образом, правило modus ponens, примененное к тавтологиям, приводит к тавтологиям. Следовательно, всякая теорема теории  есть тавтология.
есть тавтология.
Следующая лемма необходима для доказательства обратного утверждения.
Лемма 1: Пусть  есть формула,
есть формула, 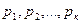 - пропозиционные переменные, входящие в формулу
- пропозиционные переменные, входящие в формулу  . Пусть задано некоторое распределение истинностных значений для переменных
. Пусть задано некоторое распределение истинностных значений для переменных 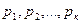 . Пусть
. Пусть 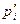 есть
есть  , если
, если 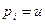 ; пусть
; пусть 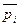 есть
есть  , если
, если 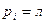 . Пусть, наконец,
. Пусть, наконец, 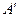 - есть
- есть  , если при этом распределении
, если при этом распределении  принимает значение и, и
принимает значение и, и 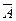 , если
, если  принимает значение л. Тогда
принимает значение л. Тогда  ├
├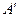 .
.
Если, например,  , то можно рассмотреть таблицу истинности данной формулы:
, то можно рассмотреть таблицу истинности данной формулы:
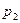
| 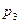
| 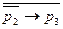
|
| И | И | Л |
| Л | И | Л |
| И | Л | Л |
| Л | Л | И |
Лемма утверждает, что факт соответствующей выводимости для каждой строки таблицы истинности. В частности, третьей строке соответствует утверждение: 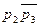 ├
├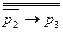 , а четвёртой строке -
, а четвёртой строке - 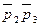 ├
├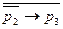 .
.
Доказательство: Докажем лемму индукцией по числу  вхождений логических операций в формулу
вхождений логических операций в формулу  (предполагается, что формула
(предполагается, что формула  записана без сокращений).
записана без сокращений).
Если 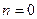 , то
, то  есть пропозиционная буква
есть пропозиционная буква 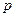 , и утверждение леммы сводится к следующему:
, и утверждение леммы сводится к следующему: 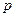 ├
├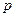 и
и 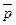 ├
├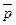 .
.
Допустим теперь, что утверждение леммы справедливо для любого числа 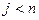 .
.
Случай 1:  имеет вид отрицания
имеет вид отрицания 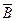 . Число вхождений логических операций в формулу
. Число вхождений логических операций в формулу  , очевидно, меньше
, очевидно, меньше  .
.
Случай 1а: Пусть при заданном распределении истинностных значений  принимает значение «истина». Тогда
принимает значение «истина». Тогда  принимает значение «ложь». Таким образом,
принимает значение «ложь». Таким образом, 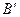 есть
есть  , и
, и 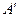 есть
есть 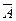 . По индуктивному допущению, применённому к
. По индуктивному допущению, применённому к  , имеем:
, имеем:  ├
├ . Следовательно, по теореме 4:
. Следовательно, по теореме 4:  . Тогда по правилу вывода
. Тогда по правилу вывода  :
:  ├
├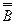 , но
, но 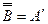 .
.
Случай 1б: Пусть  принимает значение
принимает значение 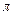 , тогда
, тогда 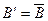 , а
, а 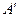 совпадает с
совпадает с 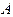 . По индуктивному предположению имеем:
. По индуктивному предположению имеем:  ├
├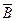 , что и требовалось доказать, ибо
, что и требовалось доказать, ибо 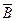 есть
есть 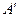 .
.
Случай 2:  имеет вид
имеет вид  , тогда число вхождений логических операций в
, тогда число вхождений логических операций в  и
и  меньше, чем в
меньше, чем в 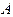 . Поэтому, в силу индуктивного допущения,
. Поэтому, в силу индуктивного допущения,  ├
├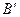 и
и  ├
├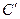 .
.
Случай 2а:  принимает значение «ложь». Тогда
принимает значение «ложь». Тогда 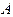 принимает значение «истина»,
принимает значение «истина», 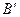 есть
есть 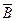 , а
, а 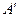 есть
есть 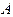 . Таким образом,
. Таким образом,  ├
├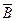 и по теореме 5
и по теореме 5 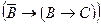 имеем:
имеем:  ├
├ . Но
. Но  и есть
и есть 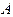 .
.
Случай 2б:  принимает значение
принимает значение  . Следовательно,
. Следовательно, 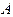 принимает значение
принимает значение  ,
, 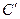 есть
есть  , а
, а 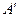 есть
есть 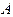 . Имеем:
. Имеем:  ├
├ , тогда по схеме аксиом (А1)
, тогда по схеме аксиом (А1) 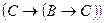 получаем:
получаем:  ├
├ , где
, где  совпадает с
совпадает с 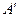 .
.
Случай 2с:  принимает значение
принимает значение  ,
,  принимает значение
принимает значение 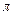 . Тогда
. Тогда 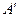 есть
есть 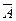 , т. к.
, т. к. 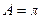 .
. 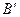 есть
есть  и
и 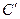 есть
есть 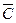 . Имеем:
. Имеем:  ├
├ и
и  ├
├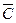 . Отсюда по теореме 8 (
. Отсюда по теореме 8 (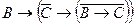 ) получаем:
) получаем:  ├
├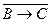 , где
, где 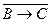 совпадает с формулой
совпадает с формулой 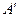 . Лемма доказана полностью.
. Лемма доказана полностью.
Теорема 11: (теорема о полноте, Кальмар).
Если формула 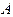 теории
теории  является тавтологией, то она является теоремой теории
является тавтологией, то она является теоремой теории  .
.
При построении любой аксиоматической теории необходимо следить, чтобы аксиоматика была непротиворечивой, т. е., чтобы из аксиом нельзя было вывести противоречия ( и
и 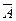 одновременно не могут быть теоремами теории
одновременно не могут быть теоремами теории  ).
).
Следствие: Теория  формально непротиворечива.
формально непротиворечива.
Доказательство: Все теоремы в теории  суть тавтологии. Отрицание тавтологии не есть тавтология. Следовательно, в
суть тавтологии. Отрицание тавтологии не есть тавтология. Следовательно, в  нет теоремы и ее отрицания.
нет теоремы и ее отрицания.
Основные понятия о формализации логики предикатов.
Отметим, что формализация логики высказываний – это лишняя работа, т. к. на все основные вопросы логики высказываний можно получить ответ, например, построив таблицу истинности.
Мы привели эту формализацию в предыдущем параграфе для того, чтобы иметь представление о формальных языках, о доказательствах в таких языках. Для других математических теорий формальный язык может быть полезен для ответа на некоторые фундаментальные вопросы. Например, является ли данная математическая теория непротиворечивой? Можно ли доказать непротиворечивость той или другой теории? Можно ли сформулировать в математической теории предложение, которое нельзя доказать и нельзя опровергнуть? Ответы на подобные вопросы нельзя получить, оставаясь в рамках традиционной классической математики.
Далее будут рассмотрены основные определения, необходимые для формализации математических теорий.
В области определения предикатов, изучаемых в математике, как правило, могут быть выделенные элементы или определены алгебраические операции. Выделенный элемент – это такой элемент, который обладает индивидуальными, только ему присущими свойствами. Например, наименьший элемент вполне упорядоченного множества, или нулевой элемент:
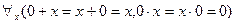 .
.
Определение 1:  - арной алгебраической операцией, определённой на множестве
- арной алгебраической операцией, определённой на множестве  , называется функция
, называется функция
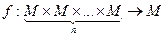 .
.
Операцию называют всюду определённой, если для всякого набора из  элементов
элементов 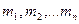 функция сопоставляет единственный элемент из множества
функция сопоставляет единственный элемент из множества  . Если функция определена не для всех наборов, то операцию называют частичной.
. Если функция определена не для всех наборов, то операцию называют частичной.
Замечание: При 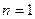 операция называется унарной, при
операция называется унарной, при 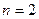 - бинарной и т. д.
- бинарной и т. д.
Например, унарная частичная операция, определённая на множестве квадратных матриц: 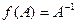 . Эта операция определена для невырожденных матриц. Операции сложения и умножения квадратных матриц данного порядка – это бинарные, всюду определённые операции.
. Эта операция определена для невырожденных матриц. Операции сложения и умножения квадратных матриц данного порядка – это бинарные, всюду определённые операции.
Если 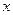 - переменная, определённая на множестве действительных чисел, то выражение
- переменная, определённая на множестве действительных чисел, то выражение 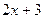 - это другая переменная, определённая на том же множестве, но для её записи необходимы постоянные величины (числа 2 и 3) и алгебраические операции (умножение и сложение).
- это другая переменная, определённая на том же множестве, но для её записи необходимы постоянные величины (числа 2 и 3) и алгебраические операции (умножение и сложение).
Аналогично выражение 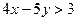 представляет двуместный предикат, определённый на множестве действительных чисел. Для его записи необходимы константы (числа 3, 4 и 5) и алгебраические операции (умножение и вычитание).
представляет двуместный предикат, определённый на множестве действительных чисел. Для его записи необходимы константы (числа 3, 4 и 5) и алгебраические операции (умножение и вычитание).
Для записи формул логики предикатов используется следующий алфавит: скобки, запятые, символы исчисления высказываний (отрицание  , импликация
, импликация 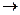 ), предметные (индивидные) переменные
), предметные (индивидные) переменные 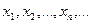 , предметные (индивидные) константы
, предметные (индивидные) константы 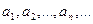 , предикатные буквы
, предикатные буквы 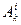 и функциональные буквы
и функциональные буквы 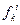 . Верхний индекс предикатной или функциональной буквы указывает на число аргументов, а нижний – служит для различия букв с одним и тем же числом аргументов.
. Верхний индекс предикатной или функциональной буквы указывает на число аргументов, а нижний – служит для различия букв с одним и тем же числом аргументов.
Функциональные буквы, применённые к константам, порождают термы. Точнее:
а) всякая предметная переменная или константа – есть терм.
б) если 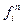 - функциональная буква и
- функциональная буква и  - термы, то
- термы, то 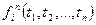 - есть терм.
- есть терм.
в) выражение является термом тогда и только тогда, когда это вытекает из пунктов а) и б).
Определим теперь формулы логики предикатов.
Предикатные буквы, применённые к термам, порождают элементарные формулы. А точнее: если 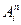 - предикатная буква, а
- предикатная буква, а  - термы, то
- термы, то 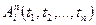 - элементарная формула.
- элементарная формула.
Определение 2: Формулы исчисления предикатов определяются следующим образом:
1) всякая элементарная формула – есть формула.
2) если  и
и  - формулы и
- формулы и  - предметная переменная, то каждое из следующих выражений есть формула:
- предметная переменная, то каждое из следующих выражений есть формула: 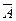 ,
,  и
и 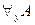 .
.
3) выражение является формулой тогда и только тогда, когда это следует из правил 1) и 2).
В выражении 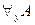 буква
буква  называется областью действия квантора общности. При этом
называется областью действия квантора общности. При этом  может и не содержать переменной
может и не содержать переменной  . В этом случае содержательный смысл
. В этом случае содержательный смысл  и
и 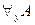 считается одинаковым.
считается одинаковым.
Выражения 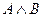 ,
, 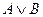 ,
,  определяются так же, как в теории
определяются так же, как в теории  . У нас нет необходимости включать в число основных символов знак квантора существования
. У нас нет необходимости включать в число основных символов знак квантора существования  , так как можно определить
, так как можно определить 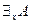 , как сокращённую запись для выражения
, как сокращённую запись для выражения 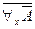 . Это полностью отражает содержательный смысл кванторов.
. Это полностью отражает содержательный смысл кванторов.
Оставляя в силе соглашение о снятии скобок, договоримся дополнительно считать, что кванторы 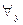 и
и 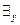 располагаются по силе между операциями
располагаются по силе между операциями 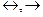 и
и 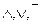 . Например, вместо выражения
. Например, вместо выражения 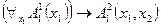 можно написать:
можно написать: 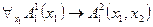 .
.
Определение 3: Вхождение переменной в данную формулу называется связным, если находится под знаком квантора общности , или в области действия входящего в эту формулу квантора. В противном случае вхождение переменной в формулу называется свободным.
Пусть 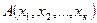 - формула, в которой переменные
- формула, в которой переменные 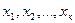 - свободные переменные. Тогда применяют запись:
- свободные переменные. Тогда применяют запись: 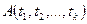 для обозначения формулы, полученной в результате подстановки термов
для обозначения формулы, полученной в результате подстановки термов 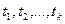 соответственно вместо свободных вхождений в формулу
соответственно вместо свободных вхождений в формулу  переменных
переменных 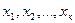 .
.
Определение 4: Терм 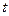 называется свободным термом для переменной
называется свободным термом для переменной 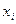 в формуле
в формуле  , если никакое свободное вхождение
, если никакое свободное вхождение 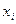 в формулу
в формулу  не лежит в области действия никакого квантора
не лежит в области действия никакого квантора 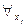 , где
, где 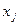 - переменная, входящая в терм
- переменная, входящая в терм 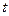 .
.
Примеры:
1) Терм 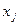 свободен для переменной
свободен для переменной 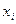 в выражении
в выражении 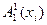 , но не свободен для этой же переменной
, но не свободен для этой же переменной 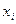 в выражении
в выражении 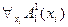 .
.
2) Терм 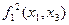 является свободным для переменной
является свободным для переменной  в выражении
в выражении 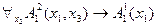 , но не свободен для переменной
, но не свободен для переменной  в выражении
в выражении 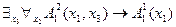 .
.
3) Если терм не содержит переменных, то он свободен для любой переменной в любой формуле.
4) Терм 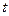 свободен для любой переменной в формуле
свободен для любой переменной в формуле  , если никакая переменная терма
, если никакая переменная терма 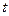 не является связной в формуле
не является связной в формуле  .
.
5) Переменная 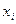 является связанной для переменной
является связанной для переменной 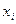 в любой формуле.
в любой формуле.
6) Всякий терм свободен для переменной 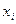 в формуле
в формуле  , если
, если  не содержит свободных вхождений переменной
не содержит свободных вхождений переменной 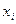 .
.
Определение 5: Под интерпретацией формулы будем понимать систему, состоящую из непустого множества  (область интерпретации) и соответствия, относящего каждой предикатной букве
(область интерпретации) и соответствия, относящего каждой предикатной букве 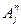 некоторое
некоторое  - местное отношение во множестве
- местное отношение во множестве  ; каждой функциональной букве
; каждой функциональной букве 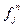 - некоторую
- некоторую  - арную операцию во множестве
- арную операцию во множестве  ; каждой предметной постоянной
; каждой предметной постоянной 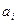 - некоторый элемент из множества
- некоторый элемент из множества  .
.
Всякая формула, не содержащая свободных переменных в любой интерпретации, является высказыванием. Если же формула содержит свободные переменные, то в любой интерпретации она является предикатом, т. к. она может быть истинной для одних значений переменных и ложной – для других.
Пусть, например, заданы следующие формулы:
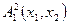 , (1)
, (1)
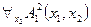 , (2)
, (2)
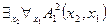 , (3)
, (3)
В качестве интерпретации этих формул рассмотрим множество натуральных чисел 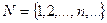 с двуместным предикатом
с двуместным предикатом 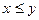 . Тогда формула (1) в этой интерпретации совпадает с предикатом
. Тогда формула (1) в этой интерпретации совпадает с предикатом 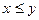 . Формула (2) в данной интерпретации является одноместным предикатом от переменной
. Формула (2) в данной интерпретации является одноместным предикатом от переменной  (переменная
(переменная  не больше любого натурального числа
не больше любого натурального числа 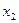 ). Область истинности данного предиката состоит из единственного наименьшего натурального числа 1. Формула (3) есть высказывание: существует число
). Область истинности данного предиката состоит из единственного наименьшего натурального числа 1. Формула (3) есть высказывание: существует число 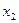 , которое меньше либо равно любого натурального числа
, которое меньше либо равно любого натурального числа  . Это – истинное высказывание, утверждающее существование наименьшего натурального числа.
. Это – истинное высказывание, утверждающее существование наименьшего натурального числа.
Определение 6: Формула  называется логически общезначимой, т. е. тавтологией (в исчислении предикатов), если она истинна в каждой интерпретации.
называется логически общезначимой, т. е. тавтологией (в исчислении предикатов), если она истинна в каждой интерпретации.
Определение 7: Формула  называется выполнимой, если существует интерпретация, в которой
называется выполнимой, если существует интерпретация, в которой  выполнима хотя бы для одного набора значений переменных.
выполнима хотя бы для одного набора значений переменных.
Очевидно, что формула  логически общезначима тогда и только тогда, когда формула
логически общезначима тогда и только тогда, когда формула 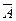 не является выполнимой. И формула
не является выполнимой. И формула  выполнима тогда и только тогда, когда формула
выполнима тогда и только тогда, когда формула 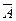 не является логически общезначимой.
не является логически общезначимой.
Как известно, во всякой интерпретации всякая замкнутая формула  (т.е. высказывание) или истинна или ложна, т.е. выполнима либо на каждом наборе переменных, либо ни на одном. Следовательно, всякая замкнутая формула
(т.е. высказывание) или истинна или ложна, т.е. выполнима либо на каждом наборе переменных, либо ни на одном. Следовательно, всякая замкнутая формула  выполнима тогда и только тогда, когда она истинна в какой-нибудь интерпретации.
выполнима тогда и только тогда, когда она истинна в какой-нибудь интерпретации.
Определение 8: Будем называть формулу  противоречием (в исчислении предикатов), если формула
противоречием (в исчислении предикатов), если формула 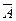 является логически общезначимой (тавтологией) или, что то же самое, если формула
является логически общезначимой (тавтологией) или, что то же самое, если формула  ложна во всякой интерпретации.
ложна во всякой интерпретации.
Определение 9: Говорят, что формула  логически влечет формулу
логически влечет формулу  , если в любой интерпретации формула
, если в любой интерпретации формула  выполнима на любом наборе, на котором выполнена формула
выполнима на любом наборе, на котором выполнена формула  .
.
Определение 10: Формулу  называют логическим следствием формул из множества
называют логическим следствием формул из множества  , если во всякой интерпретации формула
, если во всякой интерпретации формула  выполнена, если выполнены все формулы из множества
выполнена, если выполнены все формулы из множества  .
.
Определение 11: Две формулы называют логически эквивалентными, если каждая из них логически влечет другую формулу.
Например, нетрудно показать, что если формула  не содержит
не содержит 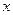 свободно, то формула
свободно, то формула  логически общезначима. Если
логически общезначима. Если 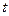 - терм, свободный для переменной
- терм, свободный для переменной 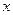 в формуле
в формуле  , то
, то 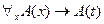 - логически общезначимая формула. А формула
- логически общезначимая формула. А формула 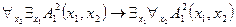 не является общезначимой. Действительно, рассмотрим в качестве основного множества интерпретации множество
не является общезначимой. Действительно, рассмотрим в качестве основного множества интерпретации множество 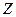 целых чисел, а двуместный предикат
целых чисел, а двуместный предикат 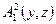 заменим неравенством
заменим неравенством 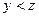 . Тогда формула
. Тогда формула 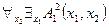 принимает значение
принимает значение  , а формула
, а формула 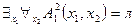 в данной интерпретации. Следовательно, импликация
в данной интерпретации. Следовательно, импликация 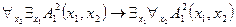 не может быть тавтологией (логически общезначимой).
не может быть тавтологией (логически общезначимой).
Из приведенных выше определений вытекают следующие утверждения:
а) Формула  логически влечет формулу
логически влечет формулу  тогда и только тогда, когда формула
тогда и только тогда, когда формула  логически общезначима.
логически общезначима.
б) Формулы  и
и  логически эквивалентны тогда и только тогда, когда формула
логически эквивалентны тогда и только тогда, когда формула  логически общезначима.
логически общезначима.
в) Если формула  логически влечет формулу
логически влечет формулу  и
и  истинна данной интерпретации, то в этой же интерпретации истинна и
истинна данной интерпретации, то в этой же интерпретации истинна и  .
.
В случае исчисления высказываний метод истинностных таблиц дает эффективный способ проверки, является ли произвольная формула тавтологией. Доказано, что для исчисления предикатов не существует эффективного способа проверки того, что произвольная формула является логически общезначимой.
Таким образом, аксиоматический метод, который был «излишней роскошью» при изучении исчисления высказываний, представляется необходимым при изучении формул, содержащих кванторы.
Далее будет описана аксиоматизация теории первого порядка.
Определение 12:Теорией предикатов первого порядка (или языком узкого исчисления предикатов) будем называть такую теорию, в которой не допускаются предикаты, имеющие в качестве аргументов другие предикаты или функции. В частности, не допускаются кванторы по предикатам или кванторы по функциям.
Доказано, что теорий первого порядка хватает для описания известных математических теорий. И, во всяком случае, большинство теорий высших порядков может быть «переведено» язык теорий первого порядка.
Обозначим теорию первого порядка буквой  .
.
Определение 13: Символами всякой теории  первого порядка служат те же символы, которые мы ввели для исчисления высказываний:
первого порядка служат те же символы, которые мы ввели для исчисления высказываний:
1) логические связки  (отрицание и импликация);
(отрицание и импликация);
2) знаки пунктуации;
3) счетное множество предметных переменных 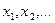 ;
;
4) непустое множество (конечное или счетное) предикатных букв 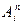
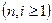 ;
;
5) конечное (возможно и пустое) или счетное множество функциональных букв 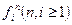 ;
;
6) конечное (тоже, возможно, пустое) или счетное множество предметных констант 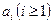 .
.
Таким образом, в различных теориях  могут отсутствовать некоторые или даже все функциональные буквы и предметные константы, а также некоторые (но не все) предикатные буквы.
могут отсутствовать некоторые или даже все функциональные буквы и предметные константы, а также некоторые (но не все) предикатные буквы.
Различные теории могут отличаться друг от друга составом символов. Определения терма, формулы, логических связок 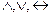 остаются в силе для любой теории первого порядка. Разумеется, в каждой конкретной теории
остаются в силе для любой теории первого порядка. Разумеется, в каждой конкретной теории  при построении термов и формул участвуют только те символы, которые принадлежат данной теории.
при построении термов и формул участвуют только те символы, которые принадлежат данной теории.
Аксиомы теории  разбиваются на два класса: логические аксиомы и собственные (или нелогические) аксиомы.
разбиваются на два класса: логические аксиомы и собственные (или нелогические) аксиомы.
Логические аксиомы: Каковы бы ни были формулы 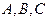 теории
теории  , следующие формулы являются логическими аксиомами:
, следующие формулы являются логическими аксиомами:
(А1) 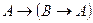 ;
;
(А2) 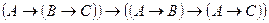 ;
;
(А3) 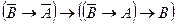 ;
;
(А4) 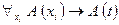 ,
,
где 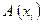 - формула теории
- формула теории  и
и 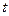 – терм этой теории, свободный для переменной
– терм этой теории, свободный для переменной 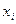 в формуле
в формуле 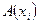 . В частности, терм
. В частности, терм 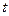 может совпадать с
может совпадать с 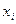 , тогда получаем аксиому
, тогда получаем аксиому 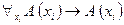 .
.
(А5) 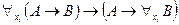 ,
,
если формула  не содержит свободного вхождения переменной
не содержит свободного вхождения переменной  .
.
Собственные аксиомы не могут быть сформулированы в общем случае, т.к. они различные для различных теорий. Например: теория частично упорядоченных множеств (в частности структур); теория натуральных чисел; теория групп в алгебре и т. д. В частности, теория первого порядка, не содержащая собственных аксиом, называется исчислением предикатов первого порядка.
Правилами вывода для всякой теории первого порядка являются:
а) Modus ponens: из  и
и  следует
следует  (сокращённо:
(сокращённо:  ).
).
б) Правило обобщения (или связывания квантором всеобщности): из  следует
следует 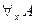 . Иногда это правило сокращённо обозначают
. Иногда это правило сокращённо обозначают  (от английского слова «generalization».
(от английского слова «generalization».
Определение 14:Моделью теории  первого порядка называется всякая интерпретация, в которой истинны все аксиомы теории
первого порядка называется всякая интерпретация, в которой истинны все аксиомы теории  .
.
Нетрудно доказать, что если правило modus ponens и правило обобщения применяются к истинным в данной интерпретации формулам, то результатом являются формулы, истинные в той же интерпретации. Следовательно, и всякая теория  истинна во всякой её модели.
истинна во всякой её модели.
Далее будет показано, что логические аксиомы выбраны так, чтобы множество всех их логических следствий из аксиом теории  в точности совпадало с множеством теорем теории
в точности совпадало с множеством теорем теории  . В частности, для исчисления предикатов первого порядка оказывается, что множество его теорем совпадает с множеством логически общезначимых формул.
. В частности, для исчисления предикатов первого порядка оказывается, что множество его теорем совпадает с множеством логически общезначимых формул.
Поясним ограничения, содержащиеся в схемах аксиом (А4) и (А5). Необходимость требования того, чтобы терм 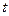 был свободен для переменной
был свободен для переменной 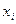 в формуле
в формуле 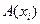 в схеме аксиом (А4) уже отмечалась выше. Для схемы (А5) отказ от требования, чтобы
в схеме аксиом (А4) уже отмечалась выше. Для схемы (А5) отказ от требования, чтобы 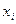 не входило свободно в формулу
не входило свободно в формулу  , также приводит к «неприятностям». Пусть, например,
, также приводит к «неприятностям». Пусть, например,  и
и  представляют собой
представляют собой 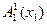 , т. е.
, т. е. 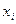 входит свободно в формулу
входит свободно в формулу  . Рассмотрим частный случай схемы (5):
. Рассмотрим частный случай схемы (5):
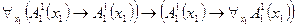 .
.
Здесь формула 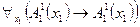 , очевидно, является общезначимой, а заключение импликации
, очевидно, является общезначимой, а заключение импликации 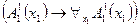 в любой интерпретации, в которой формула
в любой интерпретации, в которой формула  выполнена не для всех элементов области, не является истинным.
выполнена не для всех элементов области, не является истинным.
Примеры теорий первого порядка.
1) Теория частичного упорядочения.
Пусть  содержит единственную предикатную букву
содержит единственную предикатную букву  и не содержит функциональных букв и предметных констант. Вместо выражения
и не содержит функциональных букв и предметных констант. Вместо выражения 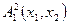 будем писать:
будем писать: 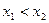 (строгое неравенство), и вместо
(строгое неравенство), и вместо 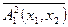 - противоположное неравенство (
- противоположное неравенство (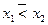 ).
).
Теория  содержит две собственные аксиомы:
содержит две собственные аксиомы:
1) 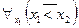 - антирефлексивность;
- антирефлексивность;
2) 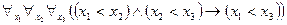 - транзитивность.
- транзитивность.
Всякую модель этой теории называют частично упорядоченным множеством.
2) Теория групп.
Пусть  имеет одну предикатную букву (равенство), одну функциональную букву
имеет одну предикатную букву (равенство), одну функциональную букву 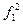 (групповая операция) и одну предметную константу
(групповая операция) и одну предметную константу  (единица группы). В соответствии с обычными обозначениями, будем писать:
(единица группы). В соответствии с обычными обозначениями, будем писать:  вместо
вместо 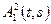 ;
; 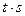 вместо
вместо 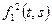 ;
;  вместо
вместо  .
.
Собственными аксиомами теории  являются формулы:
являются формулы:
1) 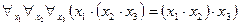 - ассоциативность умножения;
- ассоциативность умножения;
2) 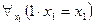 ;
;
3)  - существование обратного элемента;
- существование обратного элемента;
4) 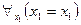 - рефлексивность равенства;
- рефлексивность равенства;
5) 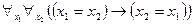 - симметричность равенства;
- симметричность равенства;
6) 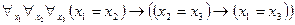 - транзитивность равенства;
- транзитивность равенства;
7) 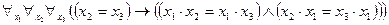 - подстановочность равенства.
- подстановочность равенства.
Всякая модель этой теории называется группой. Если в группе истинна формула 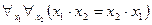 , то группа называется коммутативной (или абелевой). В этом случае операция называют обычно сложением (пишут:
, то группа называется коммутативной (или абелевой). В этом случае операция называют обычно сложением (пишут: 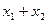 вместо
вместо 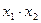 ), а единичный элемент 1 называют нулём (обозначают: 0), вместо «обратный элемент» говорят «противоположный элемент».
), а единичный элемент 1 называют нулём (обозначают: 0), вместо «обратный элемент» говорят «противоположный элемент».
Упражнения для самостоятельной работы.
1. Указать свободные и связные вхождения переменных в следующих формулах: 1) ; 2) ;Свойства теорий первого порядка.
Все результаты этого параграфа относятся к произвольной теории первого… Определение 1: Формула называется частным случаем формулы , если формула получается из формулы с помощью подстановки…Теоремы о полноте.
Теорема 1: Во всяком исчислении предикатов первого порядка всякая теорема… Доказательство: Так как частный случай тавтологии есть тавтология, то аксиомы, задаваемые схемами (А1) - (А3),…Определение 4: Всякий терм, не содержащий переменных, называется замкнутым термом.
Мы докажем это индукцией по числу логических операций и кванторов в формуле . Пусть сначала - есть замкнутая элементарная формула. В этом случае, по… Случай 1: Формула имеет вид . Если формула истинна в , то формула ложна в и,… Случай 2: Формула имеет вид импликации . Из замкнутости вытекает замкнутость и . Если формула ложна в , то и . А силу…Формальная арифметика. Система аксиом.
Пусть - теория первого порядка, в число предикатных букв которой входит .… Определение 1: Теория называется теорией первого порядка с равенством, если следующие формулы являются теоремами…Булевы функции. Основные понятия и определения. Реализация булевых функций формулами.
С точки зрения алгебры высказываний логические операции полностью характеризуются истинностными таблицами. При этом можно забыть о том, что мы рассматриваем какие-то операции над высказываниями, и иметь дело лишь с самими таблицами. Таблицу можно рассматривать, как способ задания некоторой функции. Таким образом, мы приходим к понятию функции алгебры логики, которое и будем исследовать в дальнейшем. Однако полезно не забывать об указанных интерпретациях логических связок.
В отличие от алгебры высказываний мы будем дальше употреблять следующие обозначения: 1 и 0 вместо привычных символов и – «истина», л – «ложь». При этом если нет никакой оговорки, мы не будем вкладывать «арифметический смысл» в эти символы.
Будем исходить из счетного алфавита переменных  .
.
Определение 1: Пусть 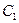 обозначает множество всех функций
обозначает множество всех функций 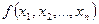 , переменные которых определены на множестве
, переменные которых определены на множестве 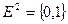 и таких, что
и таких, что 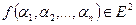 , если
, если 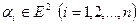 . Функции из множества
. Функции из множества 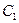 будем называть функциями алгебры логики (или булевыми функциями).
будем называть функциями алгебры логики (или булевыми функциями).
Таким образом, все булевы функции принимают свои значения из множества 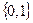 , т. е. могут быть истинными или ложными.
, т. е. могут быть истинными или ложными.
Замечание: В общем случае логические переменные могут принимать одно из 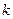 значений. Такая логика называется
значений. Такая логика называется 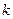 - значной логикой. Перечень всех
- значной логикой. Перечень всех 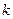 символов
символов 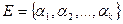 составляет алфавит, а сами символы
составляет алфавит, а сами символы 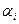 - буквы алфавита.
- буквы алфавита.
Определение 2: Функция 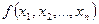 полностью определена, если задана таблица, содержащая всевозможные варианты значений переменных (наборы) и соответствующие им значения функции.
полностью определена, если задана таблица, содержащая всевозможные варианты значений переменных (наборы) и соответствующие им значения функции.
Число всех функций, зависящих от  переменных, конечно и равно
переменных, конечно и равно 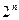 . Поэтому, для выяснения свойств данной функции достаточно просмотреть её таблицу. Однако с ростом числа аргументов таблица сильно усложняется. Для устранения этого недостатка введем следующее определение.
. Поэтому, для выяснения свойств данной функции достаточно просмотреть её таблицу. Однако с ростом числа аргументов таблица сильно усложняется. Для устранения этого недостатка введем следующее определение.
Определение 3: Будем говорить, что функция существенно зависит от переменной , если найдутся два набора, отличающиеся только - й переменной: и такие, что . Переменная называется существенной для функции . Все переменные, от которых функция не зависит существенно, называются фиктивными.
Определение 4: Число всех переменных, от которых функция зависит существенно, называется порядком функции.
Определение 5: Две функции называются равными, если одна из них может быть получена из другой путем добавления или изъятия некоторых фиктивных переменных.
Замечание: Из сказанного следует, что если задана конечная система функций  из множества
из множества  , то можно считать, что все эти функции зависят от одних и тех же переменных. С другой стороны, если дана функция, отличная от константы, то путем отождествления переменных из неё можно получить равную ей функцию, все переменные которой являются существенными.
, то можно считать, что все эти функции зависят от одних и тех же переменных. С другой стороны, если дана функция, отличная от константы, то путем отождествления переменных из неё можно получить равную ей функцию, все переменные которой являются существенными.
Для дальнейшего изложения введём в рассмотрение следующие элементарные функции:  ,
,  ,
, 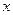 ,
, 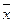 ,
, 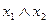 ,
, 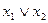 ,
, 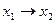 ,
, 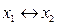 ,
, 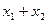 (сложение по модулю 2),
(сложение по модулю 2), 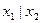 (штрих Шеффера). Определение и логическое значение каждой из этих функций было приведено выше. Отметим только, что функция
(штрих Шеффера). Определение и логическое значение каждой из этих функций было приведено выше. Отметим только, что функция 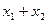 равна отрицанию эквивалентности, а функция
равна отрицанию эквивалентности, а функция 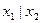 равна отрицанию конъюнкции. Функции
равна отрицанию конъюнкции. Функции  и
и 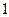 называются константами. Константы не зависят от переменных.
называются константами. Константы не зависят от переменных.
Замечание: Далее вместо символа 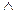 будем употреблять символ умножения или, как в обычной алгебре, знак этой операции будем опускать. Символы
будем употреблять символ умножения или, как в обычной алгебре, знак этой операции будем опускать. Символы 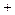 и
и 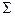 в дальнейшем будут употребляться для обозначения сложения по
в дальнейшем будут употребляться для обозначения сложения по  , при этом, исходя из определения:
, при этом, исходя из определения: 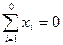 . Можно также отметить, что константы
. Можно также отметить, что константы  и
и  не зависят ни от одной переменной, следовательно, имеют нулевой порядок.
не зависят ни от одной переменной, следовательно, имеют нулевой порядок.
Как и в элементарной алгебре, исходя из «элементарных» функций, можно строить формулы.
Пусть имеется счетное множество  переменных
переменных 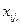 , где
, где 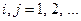 . Рассмотрим конечную или счетную систему функций алгебры логики над этим множеством:
. Рассмотрим конечную или счетную систему функций алгебры логики над этим множеством:
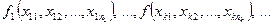 . (*)
. (*)
Введем понятие формулы над этой системой функций.
Определение 6 (интуитивное):
1. Выражение 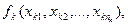
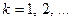 называется формулой над рассматриваемой системой функций.
называется формулой над рассматриваемой системой функций.
2. Выражение 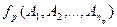 называется формулой над системой функций (*), если
называется формулой над системой функций (*), если 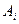 – формула или переменная из множества
– формула или переменная из множества  , а
, а 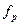 – произвольная функция из системы (*).
– произвольная функция из системы (*).
Сопоставим каждой формуле функцию алгебры логики.
Определение 7 (индуктивное):
1. Формуле 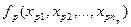 , где
, где 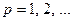 сопоставим функцию
сопоставим функцию 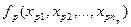 , где
, где 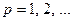 .
.
2. Формуле 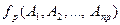 , где выражения
, где выражения 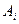 при
при 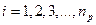 являются либо формулами, либо переменными из множества
являются либо формулами, либо переменными из множества  , а
, а 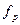 – функция системы (*), поставим в соответствие функцию
– функция системы (*), поставим в соответствие функцию 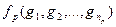 . Здесь, если
. Здесь, если 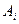 – переменная, то
– переменная, то 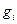 совпадает с
совпадает с 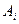 ; если
; если 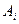 – формула, то
– формула, то 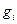 – функция, сопоставленная этой формуле.
– функция, сопоставленная этой формуле.
Полученные в соответствии с этим определением функции называются суперпозициями функций системы (*). Примеры формул: 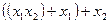 ,
, 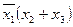 ,
, 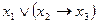 .
.
Будем говорить, что функция 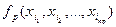 получена из функции
получена из функции 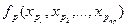 путем переименования переменных.
путем переименования переменных.
Например, функция 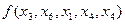 получена из функции
получена из функции 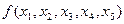 путем переименования переменных.
путем переименования переменных.
Нетрудно видеть, что при переименовании переменных возможно появление новых переменных, исчезновение старых переменных, перестановка переменных местами и отождествление переменных.
Если функция 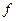 соответствует формуле
соответствует формуле  , то говорят, что формула
, то говорят, что формула  реализует функцию
реализует функцию 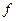 . Поскольку функции рассматриваются с точностью до фиктивных переменных, то будем считать, что формула
. Поскольку функции рассматриваются с точностью до фиктивных переменных, то будем считать, что формула 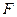 реализует и любую функцию, равную
реализует и любую функцию, равную 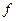 . Функция
. Функция  , соответствующая формуле
, соответствующая формуле 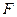 , и есть суперпозиция.
, и есть суперпозиция.
Пусть формула 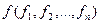 построена из функций
построена из функций 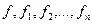 . Можно считать, что функции
. Можно считать, что функции  зависят от одних и тех же переменных.
зависят от одних и тех же переменных.
Определение 8: Две формулы называются эквивалентными, если им сопоставлены равные функции.
Эквивалентные формулы будем соединять знаком равенства.
Например, формулы 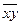 и
и 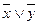 реализуют каждая функцию
реализуют каждая функцию 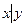 . Поэтому
. Поэтому 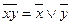 . Аналогично:
. Аналогично:  .
.
Ниже будет рассмотрена очень важная теорема, называемая теоремой о разложении. Для её формулировки примем следующие обозначения: 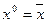 ,
, 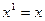 . Легко заметить, что если
. Легко заметить, что если 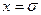 , то
, то 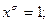 если
если 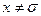 , то
, то 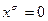 , где
, где 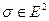 .
.
Теорема 1 (о разложении): Пусть 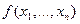 – произвольная функция алгебры логики. Тогда ее можно представить в следующей форме:
– произвольная функция алгебры логики. Тогда ее можно представить в следующей форме:
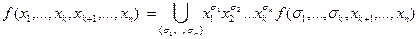 . (**)
. (**)
(Здесь мы употребляем сокращенную запись 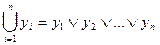 ).
).
Доказательство: Заметим сначала, что 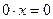 и что
и что 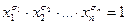 тогда и только тогда, когда
тогда и только тогда, когда 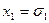 ,
, 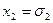 ,...,
,..., 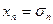 . Рассмотрим теперь произвольные
. Рассмотрим теперь произвольные 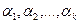 и пусть
и пусть 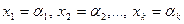 . Тогда в левой части соотношения получим
. Тогда в левой части соотношения получим 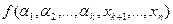 . Правая часть в силу сделанного замечания также дает
. Правая часть в силу сделанного замечания также дает 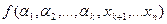 . Теорема доказана.
. Теорема доказана.
Большое практическое значение имеют следствия из этой теоремы.
Следствие 1: Если 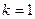 , то представление (**) принимает следующий вид:
, то представление (**) принимает следующий вид: 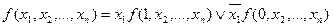 .
.
Следствие 2: Если 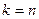 , то представление (**) превращается в следующее равенство:
, то представление (**) превращается в следующее равенство:
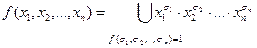 .
.
Это разложение называется совершенной дизъюнктивной нормальной формой (С.Д.Н.Ф.) функции 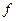 . Оно определено для любой функции
. Оно определено для любой функции 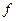 из множества булевых функций
из множества булевых функций  , не равной константе
, не равной константе  .
.
Определение замкнутого класса.
Принцип двойственности.
Пусть – некоторое подмножество множества булевых функций: . Определение 1: Множество называется замыканием множества , если оно содержит все суперпозиции функций множества и не…Многочлены Жегалкина.
Линейные функции. Монотонные функции.
Рассмотрим систему функций: , , , . (***)Теорема Поста.
В предыдущем параграфе были рассмотрены некоторые классы булевых функций. В… — класс булевых функций, сохраняющих 0;Упражнения для самостоятельной работы.
2) Сколько имеется различных функций алгебры логики от n переменных?Список литературы.
1) Э. Мендельсон. Введение в математическую логику (пер. с англ.), М., Наука, 1971.
2) Р.Л. Гудстейн. Математическая логика (пер. с англ.), М., Иностранная литература, 1961.
3) П.С. Новиков. Конструктивная математическая логика с точки зрения классической, М., Наука, 1977.
4) И.А. Лавров, Л. Л. Максимова. Задачи по теории множеств, математической логике и теории алгоритмов, М., Наука, 1975.
5) С. Клини. Математическая логика (пер. с англ.), М., Мир, 1973.
6) С.В. Яблонский. Введение в дискретную математику, М., Наука, 1986.
7) Р. Столл. Множества. Логика. Аксиоматические теории. М., Просвещение, 1968.
– Конец работы –
Используемые теги: курс, лекций, математической, логике0.08
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: КУРС ЛЕКЦИЙ ПО МАТЕМАТИЧЕСКОЙ ЛОГИКЕ
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов