Некоторые схемы доказательства теорем.
Многие теоремы в математике имеют форму импликации  . В этом случае условие
. В этом случае условие  называют достаточным для условия
называют достаточным для условия  , а условие
, а условие  – необходимым для условия
– необходимым для условия  .
.
Рассмотрим для примера известную из планиметрии теорему: «Если в треугольнике боковые стороны равны, то в этом треугольнике углы при основании равны». Разобьём формулировку теоремы на два высказывания:  = «В треугольнике боковые стороны равны»,
= «В треугольнике боковые стороны равны»,  = «В треугольнике углы при основании равны». Тогда видно, что данная теорема имеет вид импликации
= «В треугольнике углы при основании равны». Тогда видно, что данная теорема имеет вид импликации  . Пусть
. Пусть  - множество всех треугольников,
- множество всех треугольников, 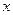 - любой элемент из множества
- любой элемент из множества  . Тогда последнюю импликацию можно обобщить для произвольного треугольника:
. Тогда последнюю импликацию можно обобщить для произвольного треугольника:
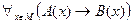 . (1)
. (1)
(1) – логическая структура теоремы.
Кроме прямой теоремы  рассматриваются ещё три:
рассматриваются ещё три:
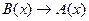 (2)
(2)
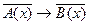 (3)
(3)
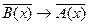 (4)
(4)
Если (1) – прямая теорема, (2) – обратная к теореме (1). Если имеет место теорема (1), то это не значит, что теорема (2) также имеет место. Теорема (3) является противоположной к теореме (1). Теорема (4) – теорема, обратная к противоположной.
В силу закона контрапозиции:  , теоремы (1) и (4), а также (2) и (3) попарно равносильны. Поэтому вместо теоремы (1) можно доказывать равносильную ей теорему (4). В силу закона двойного отрицания, теоремы (2) и (4) являются взаимно противоположными.
, теоремы (1) и (4), а также (2) и (3) попарно равносильны. Поэтому вместо теоремы (1) можно доказывать равносильную ей теорему (4). В силу закона двойного отрицания, теоремы (2) и (4) являются взаимно противоположными.
Для некоторых предикатов 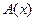 и
и 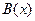 может оказаться, что имеют место и теорема (1), и теорема (2). Тогда эти две теоремы можно объединить в эквивалентность:
может оказаться, что имеют место и теорема (1), и теорема (2). Тогда эти две теоремы можно объединить в эквивалентность:
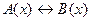 . (5)
. (5)
Такое объединение правомочно в силу следующего закона:  . Это правило показывает, что теорема (5) состоит из двух теорем: (1) и (2). Для того, чтобы доказать теорему (5), нужно доказать теорем (1) и (2) (необходимость и достаточность). Для прямой теоремы (1) принята следующая терминология: выполнение свойства
. Это правило показывает, что теорема (5) состоит из двух теорем: (1) и (2). Для того, чтобы доказать теорему (5), нужно доказать теорем (1) и (2) (необходимость и достаточность). Для прямой теоремы (1) принята следующая терминология: выполнение свойства 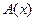 необходимо влечёт выполнение свойства
необходимо влечёт выполнение свойства 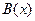 . Или: свойство
. Или: свойство 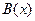 является необходимым условием свойства
является необходимым условием свойства 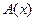 . Прямая теорема (1) часто называется необходимым условием теоремы (5). Доказательство теоремы (1) называется доказательством необходимости. Для обратной теоремы (2) принята своя терминология: свойство
. Прямая теорема (1) часто называется необходимым условием теоремы (5). Доказательство теоремы (1) называется доказательством необходимости. Для обратной теоремы (2) принята своя терминология: свойство 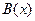 является достаточным условием выполнения свойства
является достаточным условием выполнения свойства 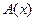 . Условие
. Условие 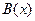 называется достаточным условием теоремы (5). Её доказательство – это доказательство достаточности. Существует другой способ доказательства теорем вида
называется достаточным условием теоремы (5). Её доказательство – это доказательство достаточности. Существует другой способ доказательства теорем вида  . Для доказательства находят последовательность эквивалентностей вида
. Для доказательства находят последовательность эквивалентностей вида 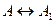 ,
, 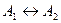 ,…,
,…, 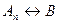 . На основании закона транзитивности отсюда можно сделать вывод об истинности данной теоремы. Кроме того, иногда доказательство теоремы «
. На основании закона транзитивности отсюда можно сделать вывод об истинности данной теоремы. Кроме того, иногда доказательство теоремы « равносильно
равносильно  » заменяют доказательством противоположной теоремы «не
» заменяют доказательством противоположной теоремы «не  равносильно не
равносильно не  ».
».