Рассмотрим некоторые схемы доказательства теорем.
1) Пусть 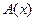 и
и 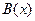 - одноместные предикаты, определённые на множестве
- одноместные предикаты, определённые на множестве  . Докажем теорему (1):
. Докажем теорему (1): 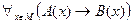 .
.
Доказательство можно построить по следующей схеме: выбрать элемент 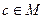 такой, что
такой, что 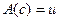 . Исходя из конкретных условий теоремы, доказывают, что из истинности высказывания
. Исходя из конкретных условий теоремы, доказывают, что из истинности высказывания 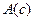 вытекает истинность высказывания
вытекает истинность высказывания 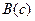 . Заключают, что импликация
. Заключают, что импликация 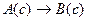 принимает значение «истина». Этим фактически заканчивается доказательство теоремы (1). В самом деле, если элемент
принимает значение «истина». Этим фактически заканчивается доказательство теоремы (1). В самом деле, если элемент 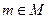 такой, что
такой, что 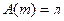 , то
, то 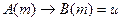 . Тогда высказывание
. Тогда высказывание 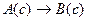 принимает значение «истина», независимо от истинностного значения высказывания
принимает значение «истина», независимо от истинностного значения высказывания 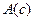 . По определению квантора общности, условие теоремы (1) выполняется для всякого элемента из множества
. По определению квантора общности, условие теоремы (1) выполняется для всякого элемента из множества  .
.
2) Схема доказательства, основанная на законе силлогизма:
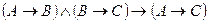 .
.
Эта формула является тавтологией. Формула 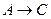 - является логическим следствием формул
- является логическим следствием формул  и
и  .
.
Иногда для доказательства теоремы (1) находят цепочку импликаций 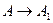 ,
, 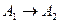 ,…,
,…, 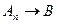 . На основании правила цепного заключения делают вывод о справедливости теоремы:
. На основании правила цепного заключения делают вывод о справедливости теоремы: .
.
3) Схема разбора случаев основана на следующей тавтологии:
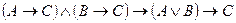 .
.
а) Если выполняется  , то
, то 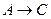 тоже выполняется.
тоже выполняется.
б) Допускаем, что существует  , и выполняется
, и выполняется  .
.
в) Если выполняется  или
или  , то формула
, то формула 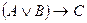 является логическим следствием формул
является логическим следствием формул 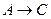 и
и  .
.
4) Доказательство от противного основано на следующем законе:
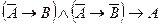 .
.
Эта тавтология используется для доказательства теорем вида 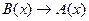 . Доказательство осуществляется следующим образом: выбирают элемент
. Доказательство осуществляется следующим образом: выбирают элемент 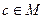 такой, что
такой, что 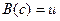 . Допускают, что высказывание
. Допускают, что высказывание 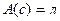 . Тогда высказывание
. Тогда высказывание 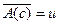 . Доказывают, что из истинности
. Доказывают, что из истинности 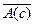 следует истинность
следует истинность 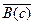 . Если
. Если 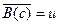 , то
, то 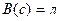 . Получили противоречие. Значит, допущение
. Получили противоречие. Значит, допущение 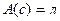 неверно. Вывод:
неверно. Вывод: 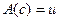 .
.
Несложно показать, что логические связки 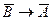 ,
, 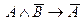 ,
, 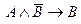 ,
, 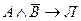 имеют ту же таблицу истинности, что и импликация
имеют ту же таблицу истинности, что и импликация  . Поэтому, иногда доказательство теоремы (1) заменяют доказательством одной из равносильных ей связок. Такой метод доказательства также называют доказательством от противного, т.к. во всех случаях предполагают, что заключение теоремы неверно и выводят отсюда противоречие.
. Поэтому, иногда доказательство теоремы (1) заменяют доказательством одной из равносильных ей связок. Такой метод доказательства также называют доказательством от противного, т.к. во всех случаях предполагают, что заключение теоремы неверно и выводят отсюда противоречие.